Coursera-deeplearning-ai-（四）

Posted on | In ,

这篇博文主要讲的是关于deeplearning.ai的第四门课程的内容，《Convolutional Neural Networks》

Week One

计算机视觉

在处理计算机视觉问题的时候，我们可能处理的图片很大，之前我们用的都是64*64*3维度的图片，这样的图片不够清晰，如果我们用1000*1000*3大小的图片，每张图片的维度就是300w，这就需要很多的数据来调参，并且对系统的资源占用非常大，此时就要用到卷积的技巧，它是卷积神经网络的基础

利用卷积进行边缘检测的示例

比如我有如下左边这张图，我想检测这张图上面有些上面，我首先要用边缘检测，分别检测出他的横向边缘和纵向边缘

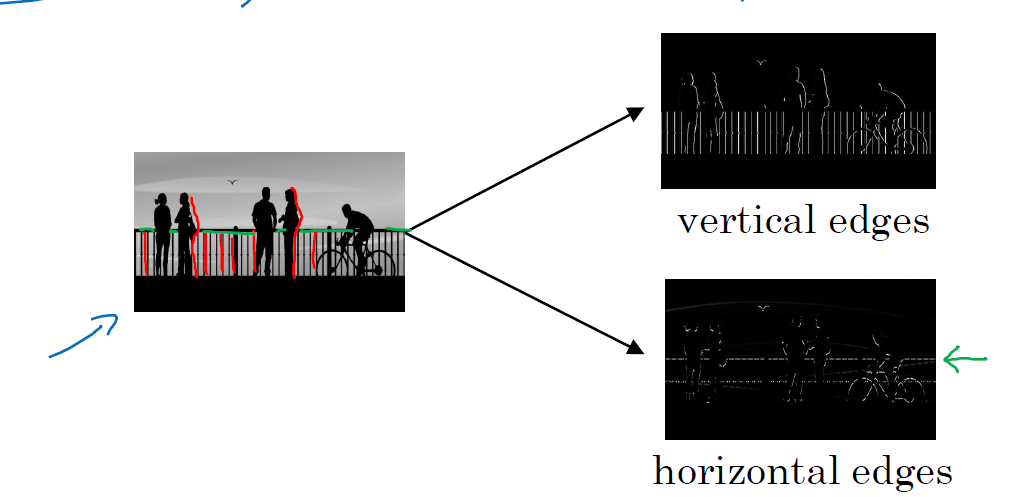
边缘检测需要用到卷积，那么上面是卷积呢？

首先，假设我们现在有一张6*6的灰度图片（仅有一个rgb通道），我们定义一个3*3的filter，当然有些地方把这个filter称为kernel，我们这里就用filter来表示，那么现在用这个3*3的filter在6*6的图像上面移动，每移动一个位置进行元素乘积求和，最终得到一个4*4的结果矩阵，如下图

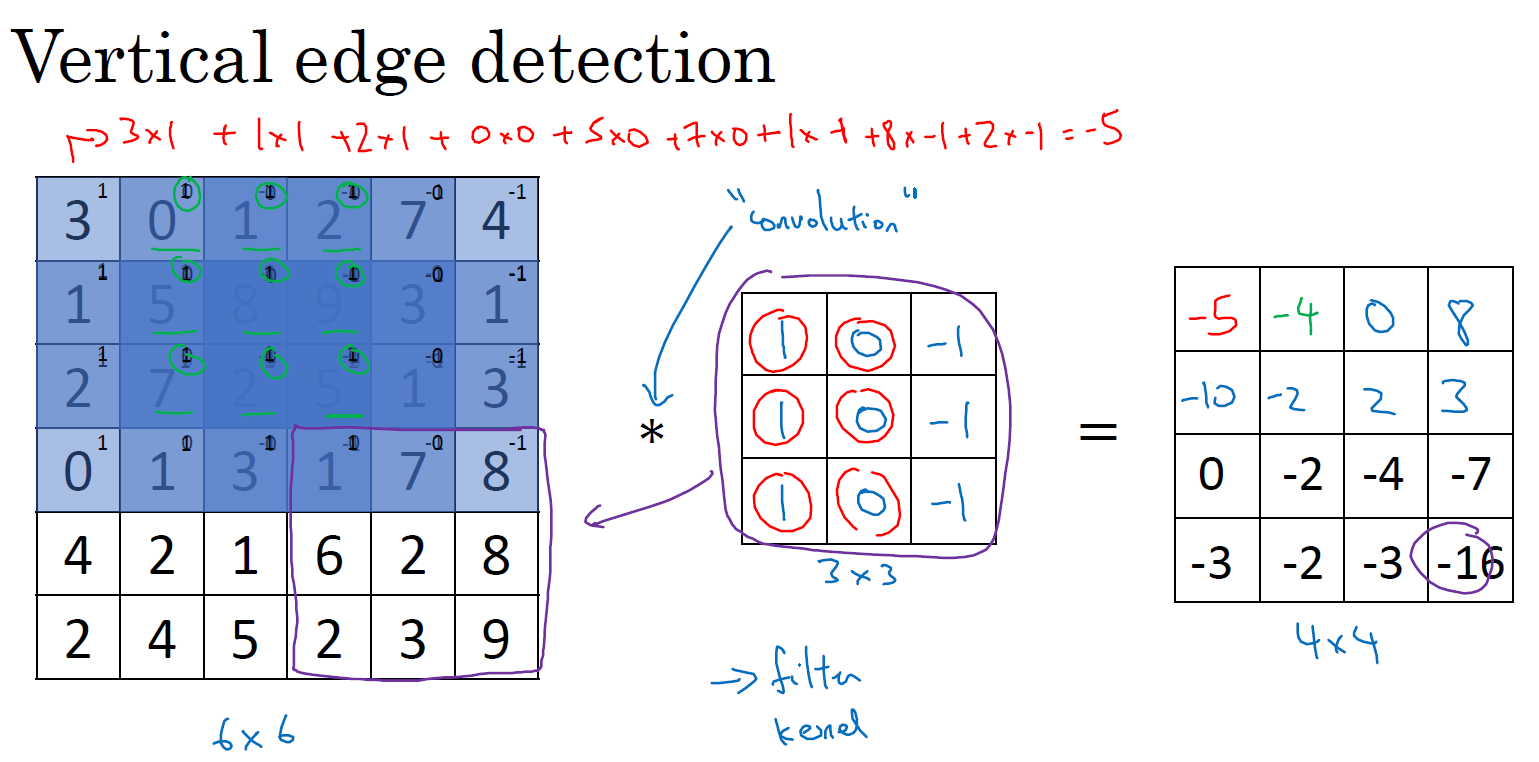
比如左上角的-5，是把3*3的矩阵放在6*6的矩阵的左上角得到的，也就是$-5=3\times1+1\times1+2\times1+0\times0+5\times0+7\times0+1\times(-1)+8\times(-1)+2\times(-1)$

然后向右移动一个单位得到-4，一直移动下去得到右边的4*4矩阵

再举一个直观的例子，比如我们现在有个黑白分明的6*6灰度图片，我们要检测它的垂直边缘，用一个3*3的filter卷积，得到一个4*4的垂直边缘结果，如下

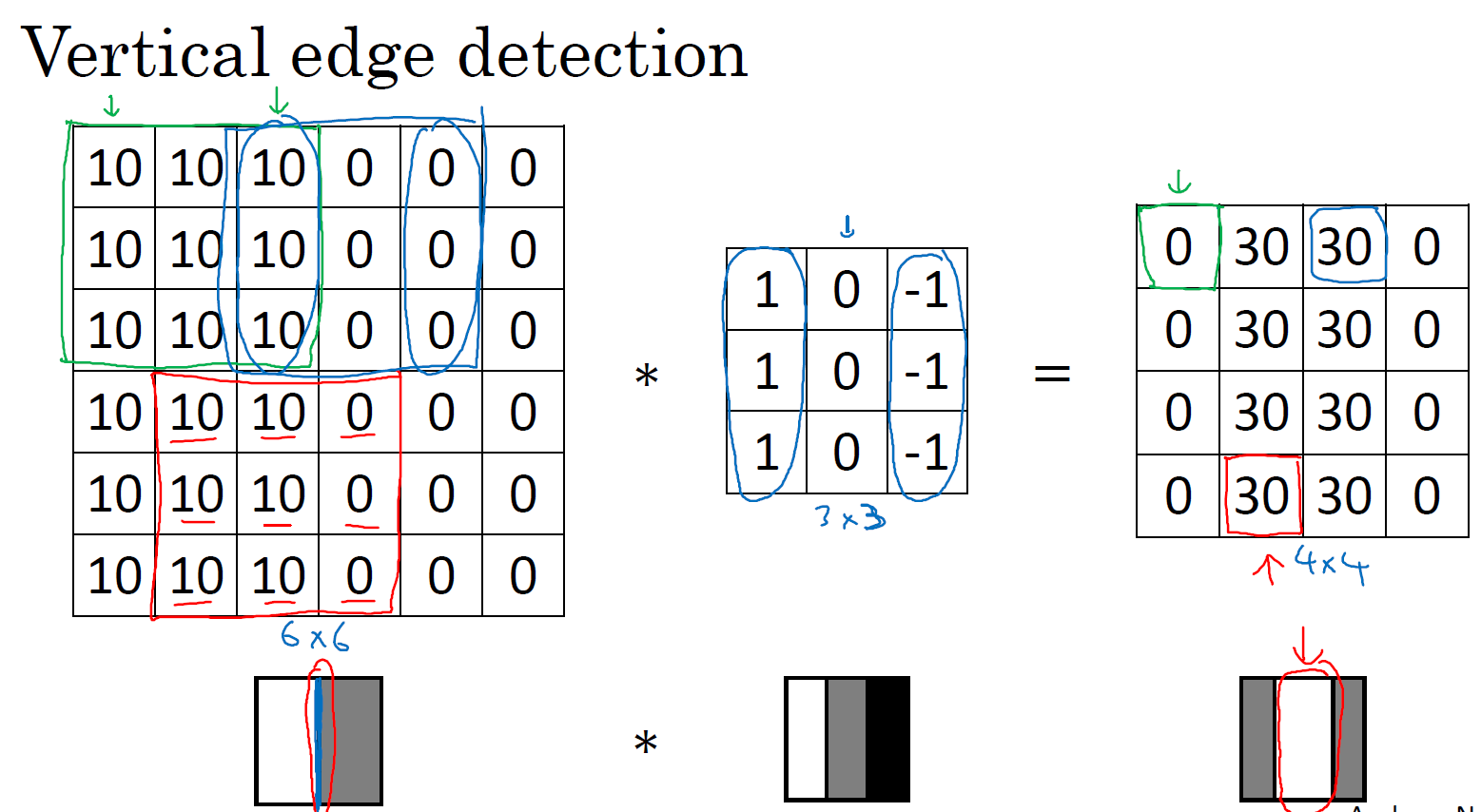
4*4矩阵中间那块白色的就是边缘，此时看起来边缘很大，那是因为我们这里的原始图片太小了，如果原始图片的大小是1000*1000，那么这个边缘就非常合理了。这里这个边缘也显示了边缘的大体趋势，是正确的

卷积函数在几乎所有深度学习框架当中都有包含，比如TensorFlow当中的tf.nn.conv2d

更多的边缘检测

边缘有着正边缘和负边缘的说法，从黑到白和从白到黑是不同的，如下图所示：

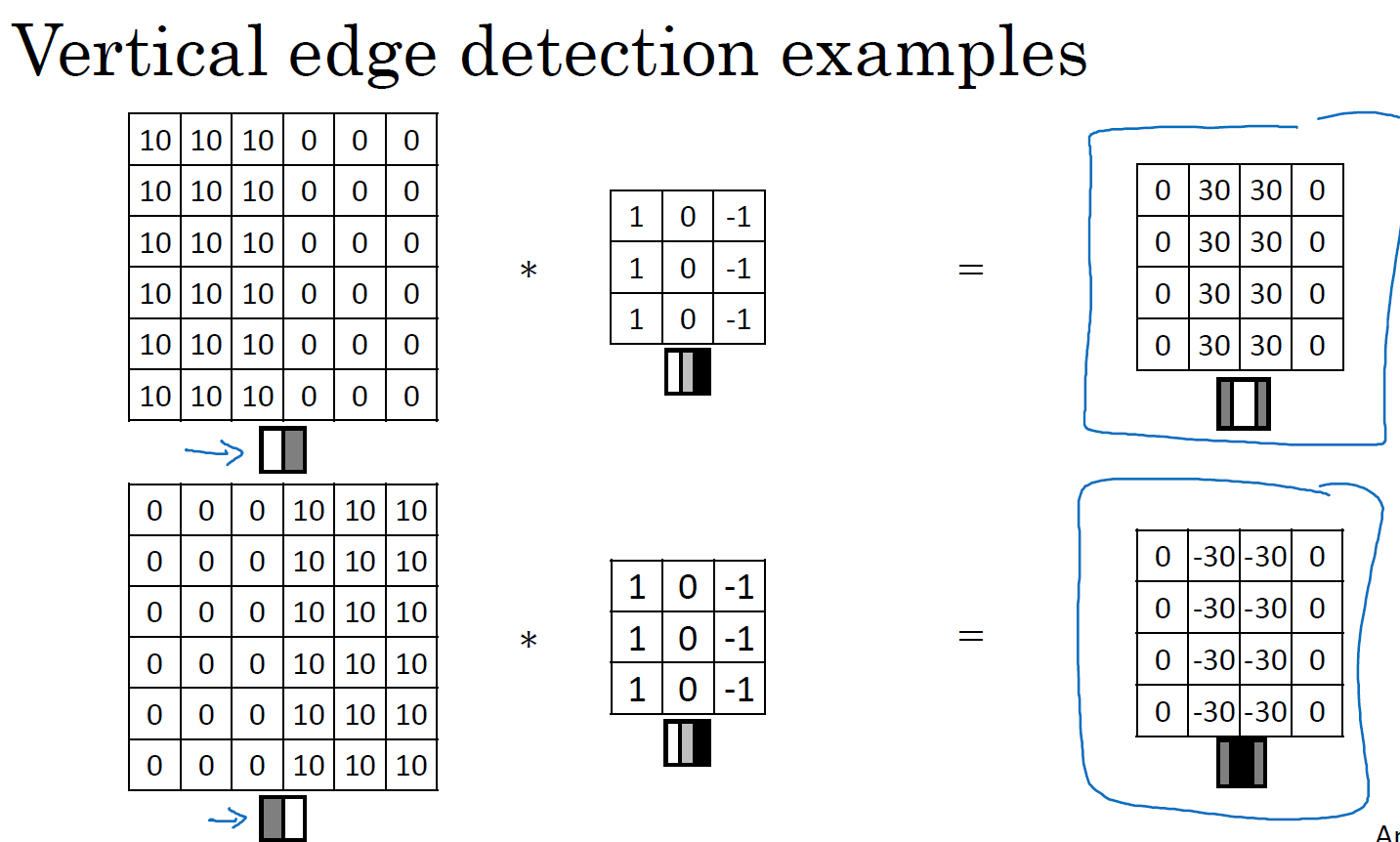
当然，还有水平边缘和垂直边缘的区分，很容易想到水平边缘的filter就是大概将竖直边缘filter转动90度

然后，根据filter使用的不同，也可以得到不同的边缘，比如常用的还有sobel filter，参数是1,2,1，还有scharr filter，参数是3,10,3，甚至你可以将这3*3的filter的9个值都设置为参数，通过反向传播来学习他们，由此你可以检测出任意角度的边缘，比如45度，70度，73度等等

padding 扩充

上面讲到的直接卷积的方法有两个明显的缺点：

  1. 图片会被缩小，你输入的是6*6的图片，最终得到的4*4的图片，比原始图片大小小了，如果经过若干层网络的卷积之后，得到的图片就相当小了
  2. 边缘信息利用得太少了，比如左上角那个像素，你在计算的过程中只会用到1次，但是中间的像素会用到很多次，那么左上角那个像素包含的信息的权重就被减小了

假设我们输入一个n*n的图片，用一个f*f的filter进行卷积，那么最终得到的是一个n-f+1的图片

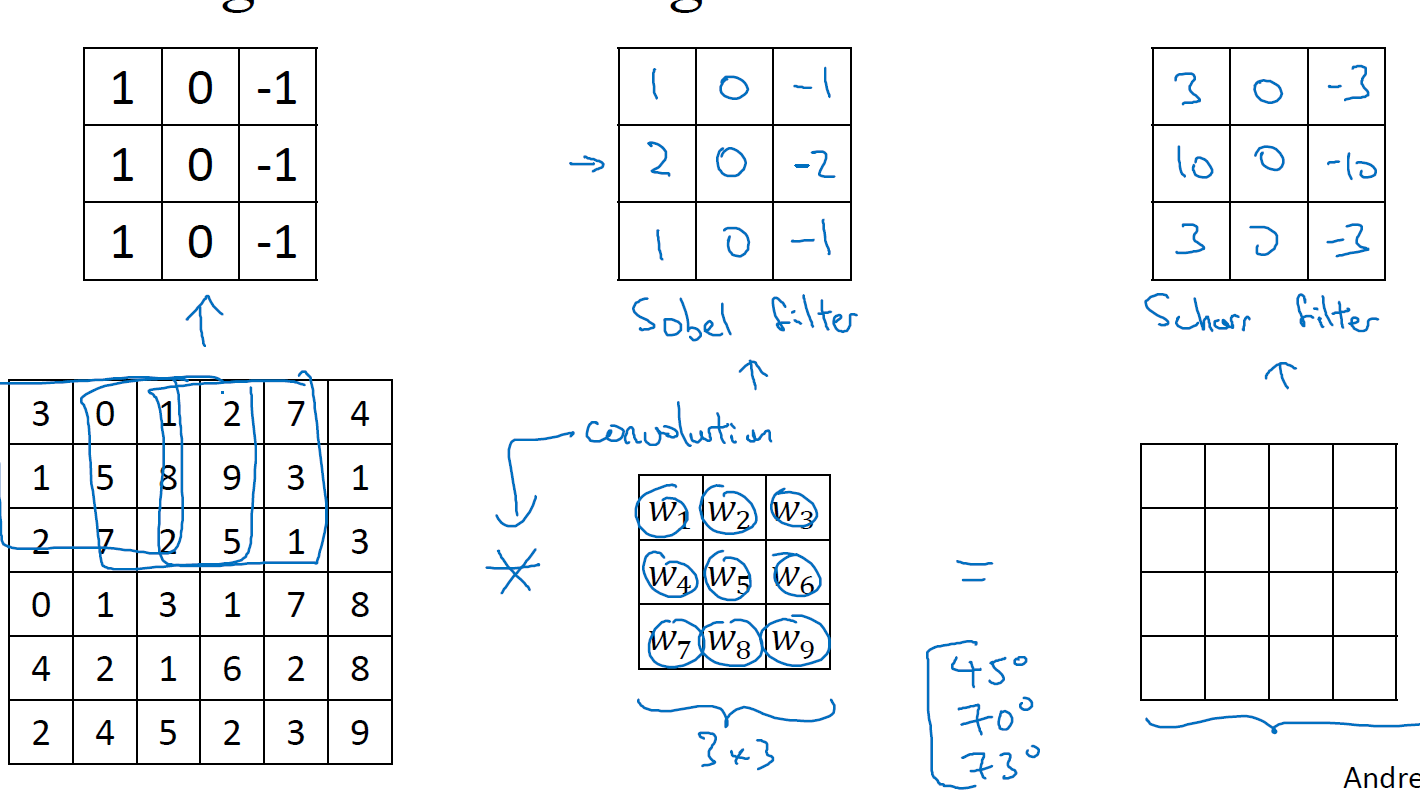
这时，我们可以使用padding的方法，一次解决上面提到的两个问题，所谓的padding就是将原来的图片向外扩充，扩充的值全部填成0，如下图所示

假如我们扩充的大小是p，那么最终得到的图片大小就是n+2p-f+1，要使得最终的图片大小等于初始大小，那么p=(f-1)/2，f通常都是一个奇数，不是奇数的时候就要混合padding，就是左右padding的范围不一样

带步长的卷积

通常的卷积是每次移动一格，但是如果你加上步长的话，每次就可以移动步长那么多格，比如你现在有一个7*7的图像，然后有个3*3的filter，如果你每次移动2步，那么最终得到的是一个3*3的图像

这个计算方法是加入你有一个n*n的图像，有一个f*f的filter，stride步长要s，padding的大小p，那么最终得到的图像大小为floor((n+2p-f)/2 +1)，其中floor表示向下取整，以防这是一个非整数的情况

我们在神经网络中用的卷积准确来说应该叫做交叉相关，真正的卷积的filter应该先向右翻转90度，再上下翻转（翻转是为了满足矩阵卷积的结合律），但是因为约定，所以我们在神经网络中的交叉相关都被称为卷积

卷积RGB图像

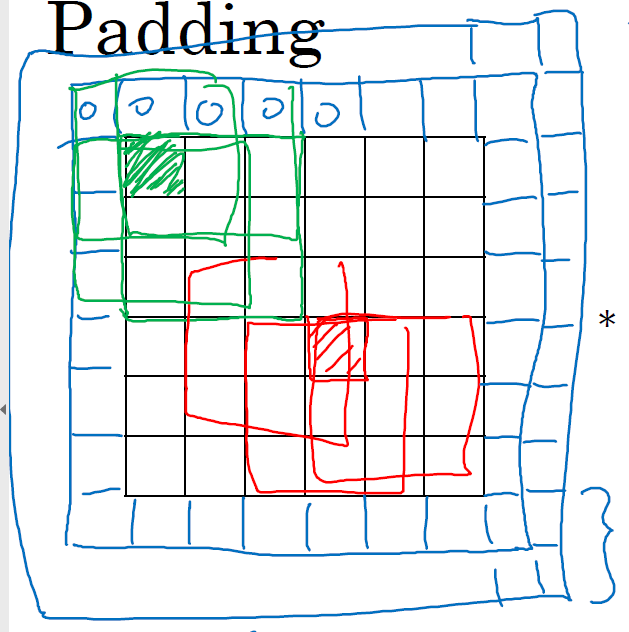
我们之前卷积的都是黑白图像，如果我们需要卷积三通道的RGB图像，我们应该怎么做呢？

如下图，在卷积RGB图像的时候，我们可以用一个同样有三通道的filter进行卷积，filter的每个通道与RGB的红绿蓝三通道相乘并全部求和，最终得到的卷积结果是只有一个通道的而不是三个通道的

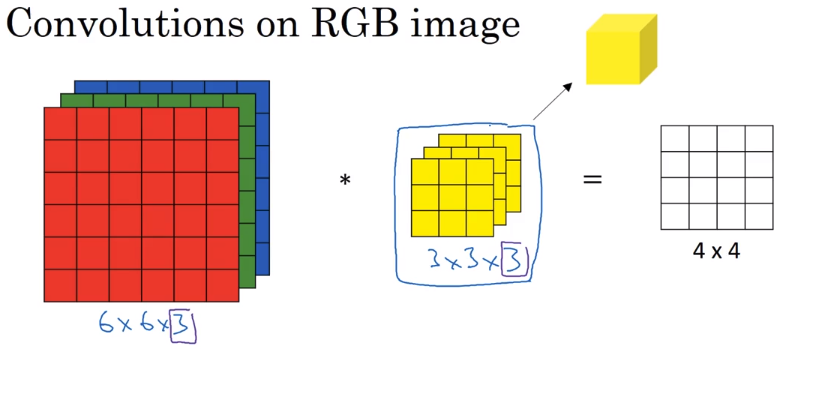
当我们需要同时取得图像的垂直边缘，水平边缘或者更多的边缘的时候，我们应该怎么做呢？

如果你需要同时取得多个边缘，你只需要同时使用多个filter即可，得到的结果是很多张边缘图，你也可以把他们stack起来

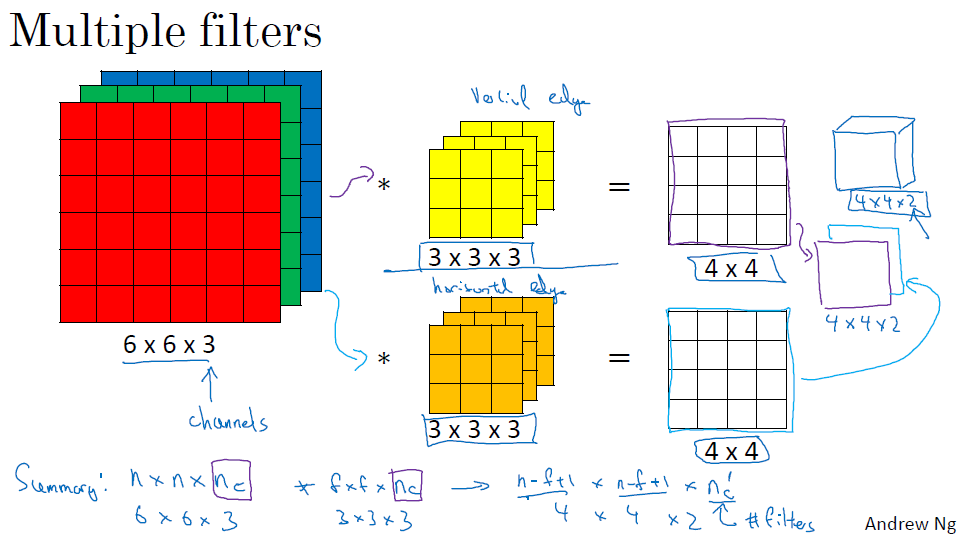
那么我们现在总结一下各个层的维度

输入的图片的维度是: $n\times n \times n_c$，其中$n_c$是指图片通道的数量

filter的维度是$f\times f \times n_c$，这里的filter的通道数和图片的通道数应该相同

得到的边缘结果的维度是$(n-f+1)\times (n-f+1) \times n_c^\prime$，其中$n_c^\prime$表示拥有的filter的数量

单层卷积神经网络

首先你输入一个RGB三通道的图像，大小是6*6*3，然后通过两个filter，大小是3*3*3，得到两个4*4的Z，分别加上bias b1,b2，然后通过Relu函数进行非线性变换，得到4*4*2

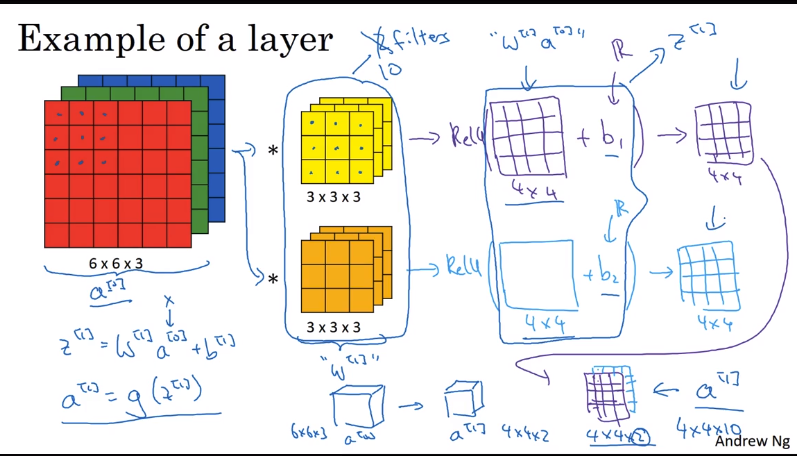
将这个单层的卷积神经网络与神经网络比较，这里的输入图像就是x,也就是$a^{[0]}$，通过的filter相当于w，之后的b相当于偏差，relu函数相当于激活函数g，得到的4*4*2的输出相当于$a^{[1]}$

让我们来看看这里面的参数及其维度

用L来表示一个卷积层，$f^{[l]}$表示filter的大小，$p^{[l]}$表示padding的大小，$s^{[l]}$表示stride的大小，$n_c^{[l]}$表示第l层filter的数量

那么输入的维度就是$n_H^{[l-1]}\times n_W^{[l-1]}\times n_c^{[l-1]}$

输出的维度是$n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]}$

其中的$n_H^{[l]}$和$n_W^{[l]}$可以用$n_H^{[l]}=\lfloor \frac{n_H^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \rfloor$来计算

每一个filter的大小是：$f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$，因为filter的通道要和输入相同

激活函数$a^{[l]}$的大小是$n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]}$，如果是批处理$A^{[l]}$的大小是$m \times n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]}$

权重w的大小是$f^{[l-1]}\times f^{[l-1]}\times n_c^{[l-1]} \times n_c^{[l]}$

偏差的大小是$n_c^{[l]}$

简单的卷积网络

下图是一个简单的神经网络的例子，输入层的维度是39*39*3，第一层的$f^{[1]}=3$，$s^{[1]}=1$，$p^{[1]}=0$，有10个filter，那么第一层的输出是37*37*10；第二层的$f^{[2]}=5$，$s^{[1]}=2$，$p^{[2]}=0$，filter个数是20，第二层的输出是17*17*20；第三层的$f^{[3]}=5$，$s^{[3]}=2$，$p^{[3]}=0$，filter个数是40，输出是7*7*40

然后，将得到的7*7*40的图像flatten成一个7*7*40=1960*1的向量，然后把这个向量输入一个logistics或softmax函数，以此进行分类

通常来说，卷积网络的图像大小会越来越小，但通道数会越来越多

卷及网络中的典型层有：

  1. Convolution (conv)
  2. Pooling（pool）
  3. Fully connected (FC)

Pooling Layers

利用pooling layer去减小表达的大小，加速计算，并使得某些特征更加稳定

pooling layer最常用的就是max pooling，就是用一个filter去移动，但是不是相乘求和，而是求出这个filter移动过程中的最大值，如下所示

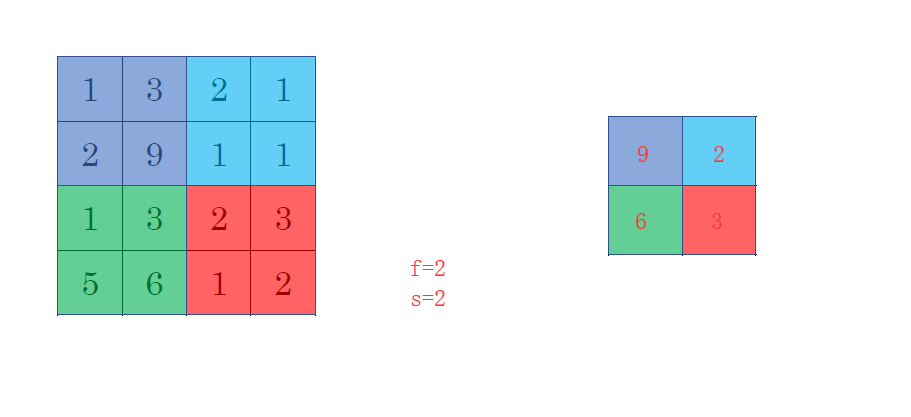
还有一种pooling叫做average pooling，不是求最大值而是平均值，这种pooling用的非常少

一个完整的卷积神经网络示例

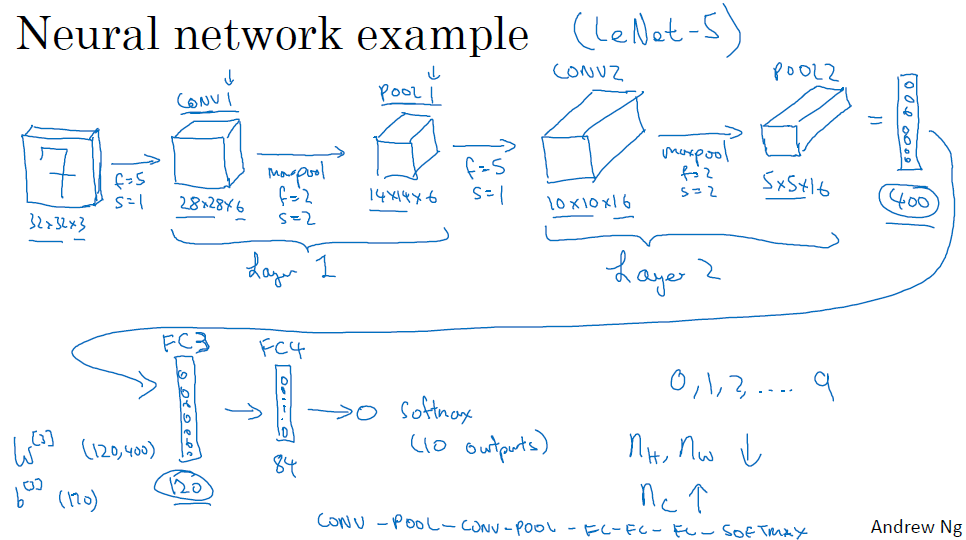
如图，我们输入一个32*32*3的网络，经过一个conv1层，f=5,s=1，得到一个28*28*6的输出，然后经一个maxpoo层pool1，得到14*14*6，这个conv1和pool1被合称为layer1，因为layer只算那些有参数的层，pool层没有参数，所以conv1和pool1合称一层layer1

然后经过conv2,f=5,s=1，得到10*10*16，然后经过pool2，得到5*5*16

此时flatten成400*1的向量，然后用普通的神经网络继续传输，此时用普通神经网络的层被称之为fully connected层，W[3]的参数是(120,400)，所以a[3]=(120,1)，然后w[4]=(84,120)，得到a[4]=(84,1)，然后经过一个softmax层，因为我们这里是分类数字0-9，所以最后的输出是(10,1)，然后选择概率最大那个

为什么要用卷积神经网络

卷积神经网络可以显著地减少参数，我们来看个例子

如下图你有一个卷积层，本来大小是32*32*3，经过一个卷积层之后大小成了28*28*6，那么你用到的参数个数应该是5*5*6+6=156个，如果你直接用全联通层，那么你需要的参数个数是32*32*3*28*28*6=14M个，明显这里的参数就非常多了

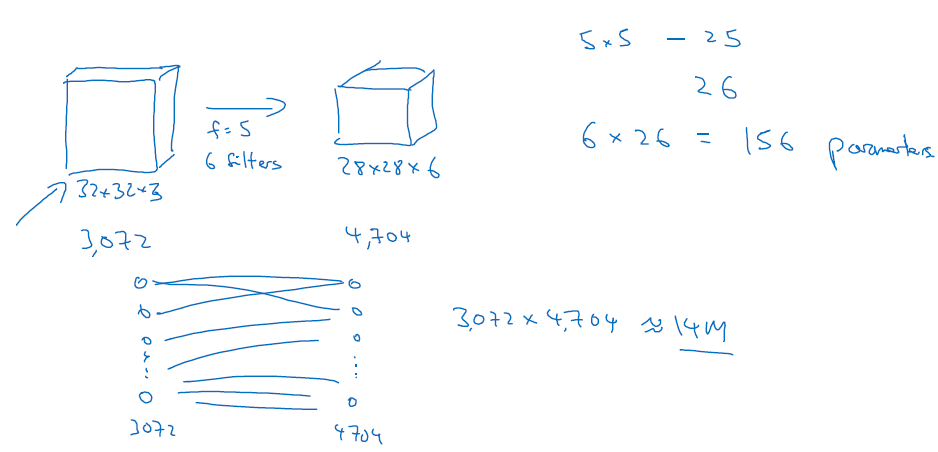
还有种解释是卷及网络有参数共享和稀疏连接的好处

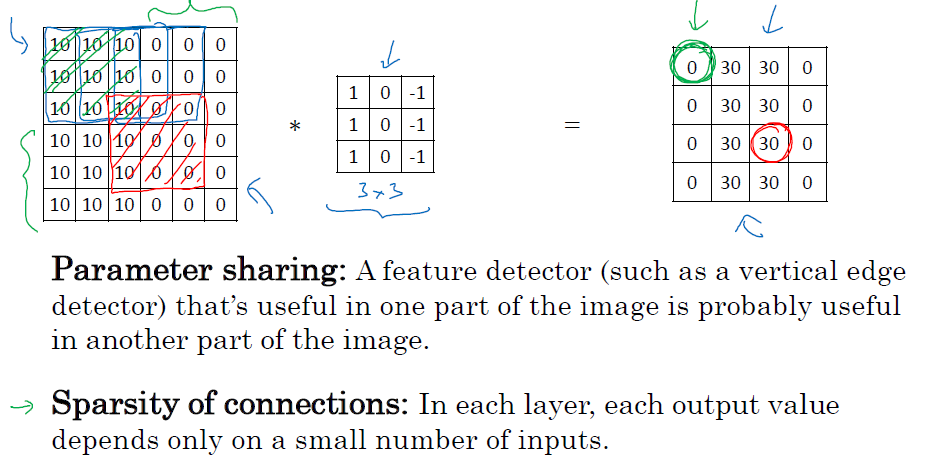
如图，你通过卷积层得到的每一个值，都只与自己的那9个卷积的值相关，与别的值不相关，这就是稀疏连接的意思，各个值之间不干扰

参数共享的意思是，比如你有一个3*3的filter，可以进行垂直边缘检测，那么这个filter无论是在同一张图的哪个地方，都可以进行边缘检测，而不是说只能在某个地方进行

利用TensorFlow搭建卷积神经网络

这周的编程作业就是利用TensorFlow搭建卷积神经网络，那么我们对程序回顾一下

read data

先看看数据读入的程序

数据是存在f5文件中的，用h5py进行读取，然后通过key访问，查看key的方法是list(data.keys())，然后访问某个key下的所有数据的方法是data['key'][:]，如果不加最后的[:]，那么你取到的是一个h5对象，然后将y reshape成一个行向量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def load_dataset():
    train_dataset = h5py.File('datasets/train_signs.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset = h5py.File('datasets/test_signs.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    classes = np.array(test_dataset["list_classes"][:]) # the list of classes
    
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
    
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

one_hot transfer

接下来是一个one_hot y label 的转换

1
2
3
def convert_to_one_hot(Y, C):
    Y = np.eye(C)[Y.reshape(-1)].T
    return Y

np.eye后面跟一个array，就可以制造一个多行的one_hot值

1
2
3
4
5
6
7
np.eye(6)[np.array([1,2,1,1,1,1])]
#array([[0., 1., 0., 0., 0., 0.],
#       [0., 0., 1., 0., 0., 0.],
#       [0., 1., 0., 0., 0., 0.],
#       [0., 1., 0., 0., 0., 0.],
#       [0., 1., 0., 0., 0., 0.],
#       [0., 1., 0., 0., 0., 0.]])

当然你也可以用tf.one_hot函数来实现

1
2
3
4
5
6
7
8
indices = [1,2,3]
depth = 3
one = tf.one_hot(indices, depth)
with tf.Session() as sess:
    print(sess.run(one))
#[[1. 0. 0.]
 #[0. 1. 0.]
 #[0. 0. 1.]]

Create Placeholder

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# GRADED FUNCTION: create_placeholders
def create_placeholders(n_H0, n_W0, n_C0, n_y):
    """
    Creates the placeholders for the tensorflow session.
    
    Arguments:
    n_H0 -- scalar, height of an input image
    n_W0 -- scalar, width of an input image
    n_C0 -- scalar, number of channels of the input
    n_y -- scalar, number of classes
        
    Returns:
    X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
    Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
    """

    ### START CODE HERE ### (≈2 lines)
    X = tf.placeholder(dtype=tf.float32,shape=(None, n_H0, n_W0, n_C0))
    Y = tf.placeholder(dtype=tf.float32,shape=(None,n_y))
    ### END CODE HERE ###
    
    return X, Y

tf.placeholder是建立占位符

None是因为不确定每次输入多少张图片，然后X的维度是height，width，n_c0，y的维度是n_y

initialize_parameters

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# GRADED FUNCTION: initialize_parameters

def initialize_parameters():
    """
    Initializes weight parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [4, 4, 3, 8]
                        W2 : [2, 2, 8, 16]
    Returns:
    parameters -- a dictionary of tensors containing W1, W2
    """
    
    tf.set_random_seed(1)                              # so that your "random" numbers match ours
        
    ### START CODE HERE ### (approx. 2 lines of code)
    W1 = tf.get_variable('W1',shape=[4,4,3,8],initializer=tf.contrib.layers.xavier_initializer(seed = 0))
    W2 = tf.get_variable('W2',shape=[2,2,8,16],initializer=tf.contrib.layers.xavier_initializer(seed = 0))
    ### END CODE HERE ###

    parameters = {"W1": W1,
                  "W2": W2}
    
    return parameters

tf.get_variable 用于建立变量，第一维的参数是f=4,个数是8个；第二维的参数是f=2，个数是16个

Forward propagation

我们这里输入parameter和X，网络的结构如下

CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED

用tf.nn.conv2d(X,W1,strides=[1, 1, 1, 1],padding='SAME')进行卷积，输入A和W，步长的输入方式是[batch,s,s,depth]，batch表示每次跳过多少张图片，depth表示跳过多少通道；padding的方法是’SAME’

每个conv2d的输出是Z，relu之后是A，maxpool之后是P

把图片flatten到一维， P2 = tf.contrib.layers.flatten(P2)

tf.contrib.layers.fully_connected(P2, num_outputs=6, activation_fn=None)表示全连接层，不用activation_fn是因为最终计算cost的时候会自动用到softmax函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
    
    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "W2"
                  the shapes are given in initialize_parameters

    Returns:
    Z3 -- the output of the last LINEAR unit
    """
    
    # Retrieve the parameters from the dictionary "parameters" 
    W1 = parameters['W1']
    W2 = parameters['W2']
    
    ### START CODE HERE ###
    # CONV2D: stride of 1, padding 'SAME'
    Z1 = tf.nn.conv2d(X,W1,strides=[1, 1, 1, 1],padding='SAME')
    # RELU
    A1 = tf.nn.relu(Z1)
    # MAXPOOL: window 8x8, sride 8, padding 'SAME'
    P1 = tf.nn.max_pool(A1,ksize=[1, 8, 8, 1],strides=[1, 8, 8, 1],padding='SAME')
    # CONV2D: filters W2, stride 1, padding 'SAME'
    Z2 = tf.nn.conv2d(P1,W2,strides=[1, 1, 1, 1],padding='SAME')
    # RELU
    A2 = tf.nn.relu(Z2)
    # MAXPOOL: window 4x4, stride 4, padding 'SAME'
    P2 = tf.nn.max_pool(A2,ksize=[1, 4, 4, 1],strides=[1, 4, 4, 1],padding='SAME')
    # FLATTEN
    P2 = tf.contrib.layers.flatten(P2)
    # FULLY-CONNECTED without non-linear activation function (not not call softmax).
    # 6 neurons in output layer. Hint: one of the arguments should be "activation_fn=None" 
    Z3 = tf.contrib.layers.fully_connected(P2, num_outputs=6, activation_fn=None)
    ### END CODE HERE ###

    return Z3

计算代价

tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y)，logists表示输出，label表示真正的标签

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# GRADED FUNCTION: compute_cost 

def compute_cost(Z3, Y):
    """
    Computes the cost
    
    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3
    
    Returns:
    cost - Tensor of the cost function
    """
    
    ### START CODE HERE ### (1 line of code)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=Z3, labels=Y))
    ### END CODE HERE ###
    
    return cost

建立model

先获取shape，然后定义placeholder

1
2
3
4
5
6
(m, n_H0, n_W0, n_C0) = X_train.shape             
n_y = Y_train.shape[1]
costs = []                                        # To keep track of the cost

# Create Placeholders of the correct shape
X, Y = create_placeholders(n_H0,n_W0,n_C0,n_y)

然后定义参数w1，w2

1
parameters = initialize_parameters()

然后进行前向传播

1
Z3 = forward_propagation(X,parameters)

然后计算cost

1
Z3 = forward_propagation(X,parameters)

设置optimizer

1
optimizer = tf.train.AdamOptimizer().minimize(cost)

进行参数初始化

1
init = tf.global_variables_initializer()

然后开始循环epochs，其中的minibatch的取法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    """
    Creates a list of random minibatches from (X, Y)
    
    Arguments:
    X -- input data, of shape (input size, number of examples) (m, Hi, Wi, Ci)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples) (m, n_y)
    mini_batch_size - size of the mini-batches, integer
    seed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.
    
    Returns:
    mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
    """
    
    m = X.shape[0]                  # number of training examples
    mini_batches = []
    np.random.seed(seed)
    
    # Step 1: Shuffle (X, Y)
    permutation = list(np.random.permutation(m))
    shuffled_X = X[permutation,:,:,:]
    shuffled_Y = Y[permutation,:]

    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:,:,:]
        mini_batch_Y = shuffled_Y[k * mini_batch_size : k * mini_batch_size + mini_batch_size,:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    # Handling the end case (last mini-batch < mini_batch_size)
    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[num_complete_minibatches * mini_batch_size : m,:,:,:]
        mini_batch_Y = shuffled_Y[num_complete_minibatches * mini_batch_size : m,:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    return mini_batches
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
# GRADED FUNCTION: model

def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
          num_epochs = 100, minibatch_size = 64, print_cost = True):
    """
    Implements a three-layer ConvNet in Tensorflow:
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
    
    Arguments:
    X_train -- training set, of shape (None, 64, 64, 3)
    Y_train -- test set, of shape (None, n_y = 6)
    X_test -- training set, of shape (None, 64, 64, 3)
    Y_test -- test set, of shape (None, n_y = 6)
    learning_rate -- learning rate of the optimization
    num_epochs -- number of epochs of the optimization loop
    minibatch_size -- size of a minibatch
    print_cost -- True to print the cost every 100 epochs
    
    Returns:
    train_accuracy -- real number, accuracy on the train set (X_train)
    test_accuracy -- real number, testing accuracy on the test set (X_test)
    parameters -- parameters learnt by the model. They can then be used to predict.
    """
    
    ops.reset_default_graph()                         # to be able to rerun the model without overwriting tf variables
    tf.set_random_seed(1)                             # to keep results consistent (tensorflow seed)
    seed = 3                                          # to keep results consistent (numpy seed)
    (m, n_H0, n_W0, n_C0) = X_train.shape             
    n_y = Y_train.shape[1]                            
    costs = []                                        # To keep track of the cost
    
    # Create Placeholders of the correct shape
    ### START CODE HERE ### (1 line)
    X, Y = create_placeholders(n_H0,n_W0,n_C0,n_y)
    ### END CODE HERE ###

    # Initialize parameters
    ### START CODE HERE ### (1 line)
    parameters = initialize_parameters()
    ### END CODE HERE ###
    
    # Forward propagation: Build the forward propagation in the tensorflow graph
    ### START CODE HERE ### (1 line)
    Z3 = forward_propagation(X,parameters)
    ### END CODE HERE ###
    
    # Cost function: Add cost function to tensorflow graph
    ### START CODE HERE ### (1 line)
    cost = compute_cost(Z3,Y)
    ### END CODE HERE ###
    
    # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
    ### START CODE HERE ### (1 line)
    optimizer = tf.train.AdamOptimizer().minimize(cost)
    ### END CODE HERE ###
    
    # Initialize all the variables globally
    init = tf.global_variables_initializer()
     
    # Start the session to compute the tensorflow graph
    with tf.Session() as sess:
        
        # Run the initialization
        sess.run(init)
        
        # Do the training loop
        for epoch in range(num_epochs):

            minibatch_cost = 0.
            num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
            seed = seed + 1
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)

            for minibatch in minibatches:

                # Select a minibatch
                (minibatch_X, minibatch_Y) = minibatch
                # IMPORTANT: The line that runs the graph on a minibatch.
                # Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
                ### START CODE HERE ### (1 line)
                _ , temp_cost = sess.run([optimizer,cost], feed_dict={X:minibatch_X, Y: minibatch_Y})
                ### END CODE HERE ###
                
                minibatch_cost += temp_cost / num_minibatches
                

            # Print the cost every epoch
            if print_cost == True and epoch % 5 == 0:
                print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
            if print_cost == True and epoch % 1 == 0:
                costs.append(minibatch_cost)
        
        
        # plot the cost
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        # Calculate the correct predictions
        predict_op = tf.argmax(Z3, 1)
        correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
        
        # Calculate accuracy on the test set
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
        print(accuracy)
        train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
        test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
        print("Train Accuracy:", train_accuracy)
        print("Test Accuracy:", test_accuracy)
                
        return train_accuracy, test_accuracy, parameters

然后run这个optimizer和cost

1
_ , temp_cost = sess.run([optimizer,cost], feed_dict={X:minibatch_X, Y: minibatch_Y})

Week Two

经典网络

LeNet-5

这个网络是在1998年提出的，结果如下图

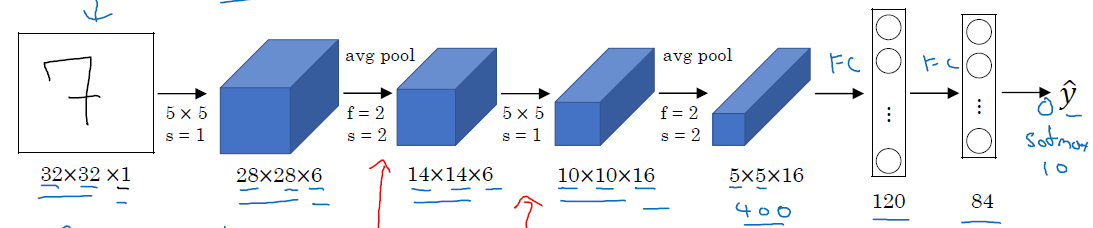
一共有大概60K个参数，第一层是6个5*5的conv layer，然后是一个f=2,s=2的pool layer（当时用的的average pool，不过后来证明max pool更有效），然后再来16个5*5的conv layer，然后是一个f=2,s=2的pool layer，然后将这个5*5*16的volume flatten为一个(400,1)的向量，经过一个fc（fully connected) layer，变成120*1,在经过一个fc layer，变成84*1的，再经过一个softmax得到一个10*1的$\hat{y}$，用于判别手写数字0-9

AlexNet

AlexNet是在2012年提出的，这个网络让人们开始觉得深度学习的确可以在图像和自然语言处理等方面表现的很好

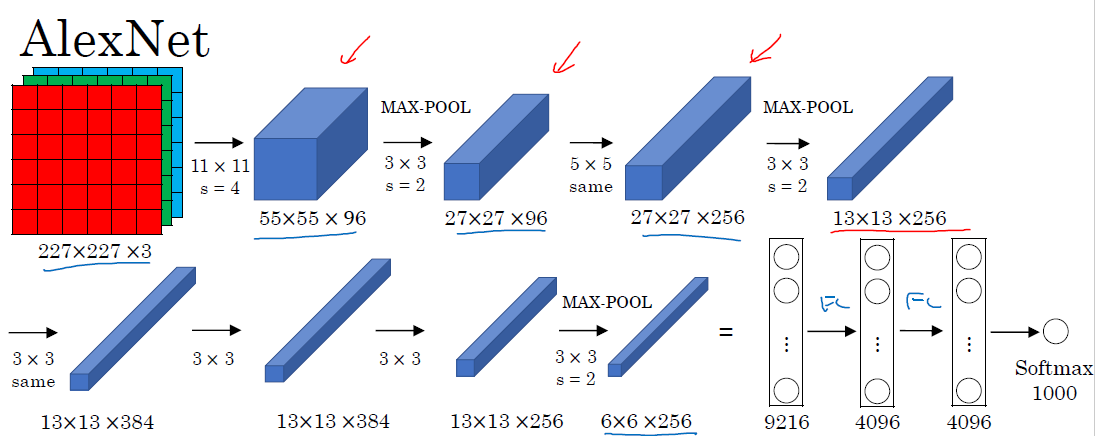
这个网络的结构是一个conv layer，跟一个max pool layer，再来一个conv layer，跟一个max-pool layer，接下来3个conv layer，跟一个max-pool layer，这时flatten为一个9216*1的向量，然后接一个FC layer，再接一个FC layer，再接一个softmax，得到输出

参数的个数为$(11113+1)96+(5596+1)256+(33256+1)384+(33384+1)3842 + 92164096 + 40964096+10004096=62811648$，约为60million个

VGG-16

这个网络在2015年提出，整个网络中用到的filter都是3*3的,padding都是same，用到的max-pool layer 都是f=2,s=2,

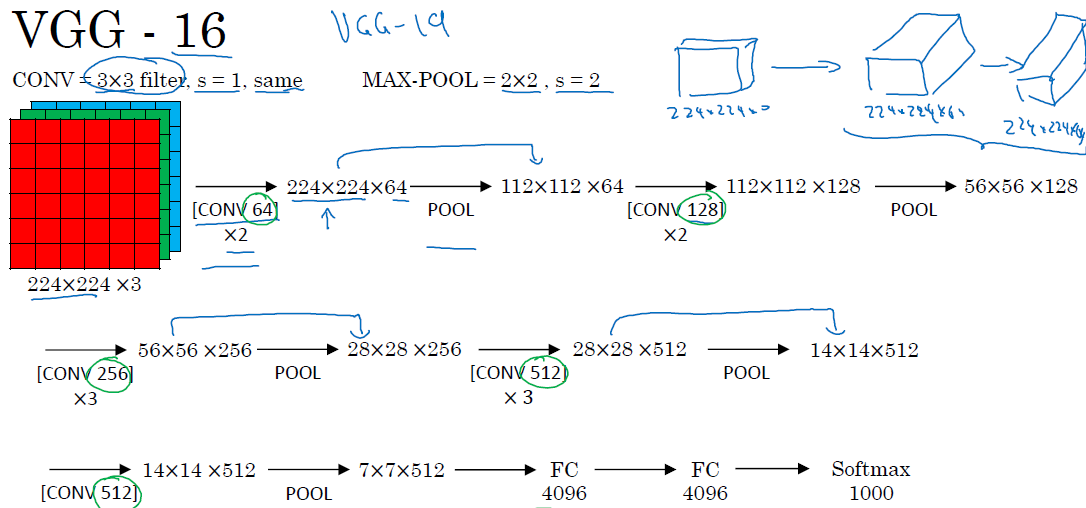
先是2层conv 64的 conv layer，然后经过一个pool layer，接下来2层128个的conv layer，接下来一个pool layer，再接下来3层256个的conv layer，接一个pool layer，再接一个3层512个的conv layer，接一个pool layer，接一层512个的conv layer，接一个pool layer，接2层FC layer，接一层softmax

为什么叫VGG-16呢，因为这个网络里有参数的层一个是16个

同时提出的还有VGG-19，但是VGG-16的效果一般来说跟VGG-19差不多，并且参数要相对少一些，所以一般都用VGG-16

VGG-16参数非常多，大概有138million个，即使对于现代计算机，计算起来也是比较吃力的

残差网络(ResNet)

残差网络首先要理解什么是残差块(Residual block)

假如你现在有一个如下的2层的神经网络，每次经过一个线性层，然后一个ReLU非线性层，到达下一层，如图所示

从左到右依次进行的被称为full path，然而如果你直接将$a^{[l]}$加到最后一个ReLU之前，这样的方法叫做short cut 或者是 skip connection，此时我们称这样一个有跳跃连接的整体为一个Residual block

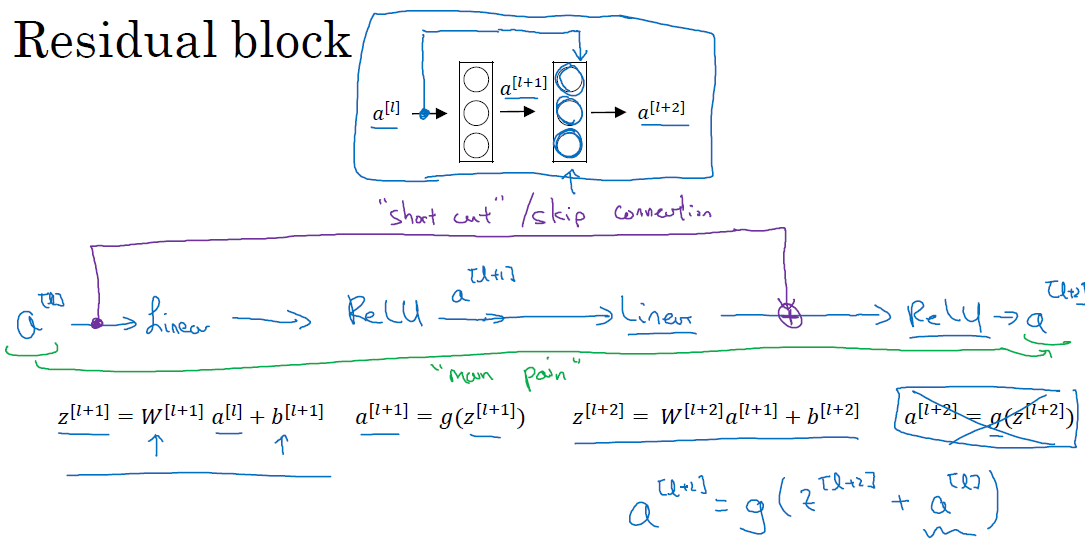
如果我们有一个10层的神经网络，每2层形成一个残差块，那么这个网络就被称为残差网络，如下图

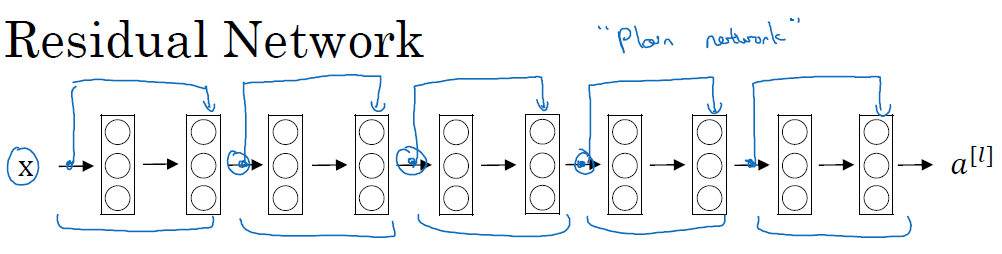
残差网络在实际中表现比普通网络更好，具体表现在：随着网络层数的增加，普通网络的训练错误会先降低后增加（因为层数增多，普通网络的训练越来越难，到后面规定的iteration还没有收敛，所以training error又增加了）；但是残差网络会一直下降，直到基本不下降的状态，不会出现training error上升的情况

我们用plain表示普通网络，ResNet表示残差网络，得到如下的training error和layers的示意图

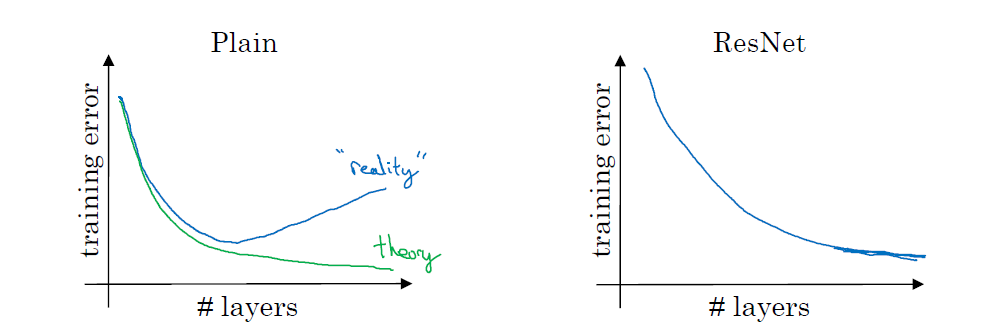
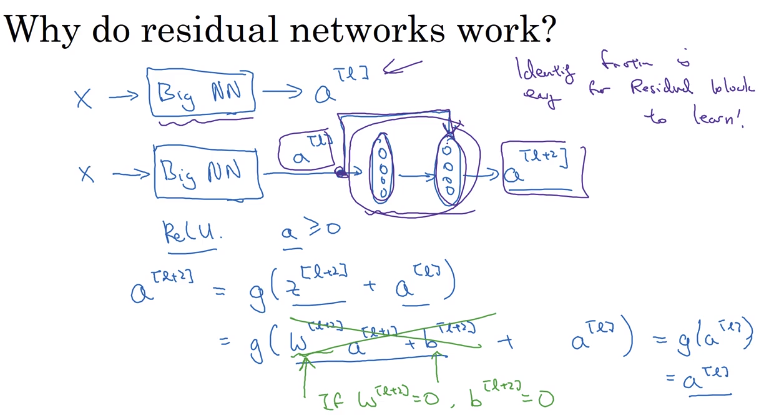
为什么残差网络可以表现得更好

  • Lets see some example that illustrates why resNet work.

    • We have a big NN as the following:

      • X --> Big NN --> a[l]

    • Lets add two layers to this network as a residual block:

      • X --> Big NN --> a[l] --> Layer1 --> Layer2 --> a[l+2]
      • And a[l] has a direct connection to a[l+2]

    • Suppose we are using RELU activations.

    • Then:

      a[l+2] = g( z[l+2] + a[l] ) = g( W[l+2] a[l+1] + b[l+2] + a[l] )

    • Then if we are using L2 regularization for example, W[l+2] will be zero. Lets say that b[l+2] will be zero too.

    • Then a[l+2] = g( a[l] ) = a[l] with no negative values.

    • This show that identity function is easy for a residual block to learn. And that why it can train deeper NNs.

    • Also that the two layers we added doesn’t hurt the performance of big NN we made.

    • Hint: dimensions of z[l+2] and a[l] have to be the same in resNets. In case they have different dimensions what we put a matrix parameters (Which can be learned or fixed)

      • a[l+2] = g( z[l+2] + ws * a[l] ) # The added Ws should make the dimentions equal
      • ws also can be a zero padding.

  • Using a skip-connection helps the gradient to backpropagate and thus helps you to train deeper networks

主要起作用的原因是redidual network 阻止了梯度消失和梯度爆炸之类的问题

$1\times 1$的卷积（network in network）

1*1的卷积主要是为了改变图片的通道数目，比如你现在有一个28*28*192的图片，你可以将它变成32通道的，以此来减少计算量，也可以把它变成192通道的，这相当于在原来的图片上加了一个192通道的图片，这将使得模型更复杂，以此来表征更加复杂的模型

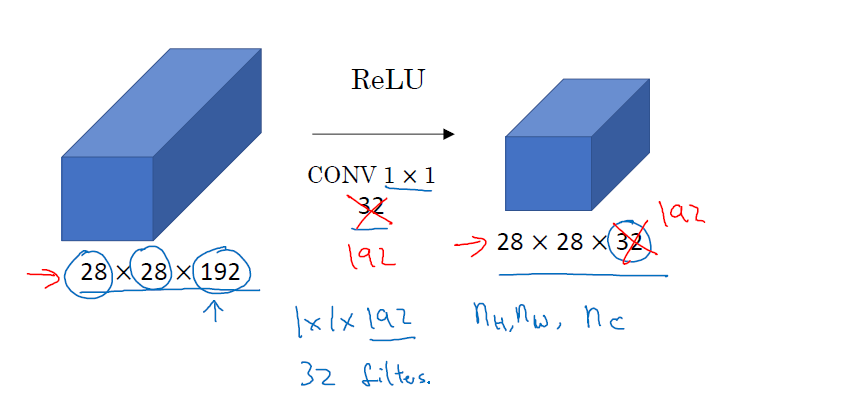
Inception Network

在设计神经网络的时候，你可能会想如何去选择conv layer 所用的filter的大小，以及max-pool的大小，这个时候其实你可以把所有你可能会想要用到的conv layer和max-pool layer联结起来，形成一个复杂的网络，具体如下：

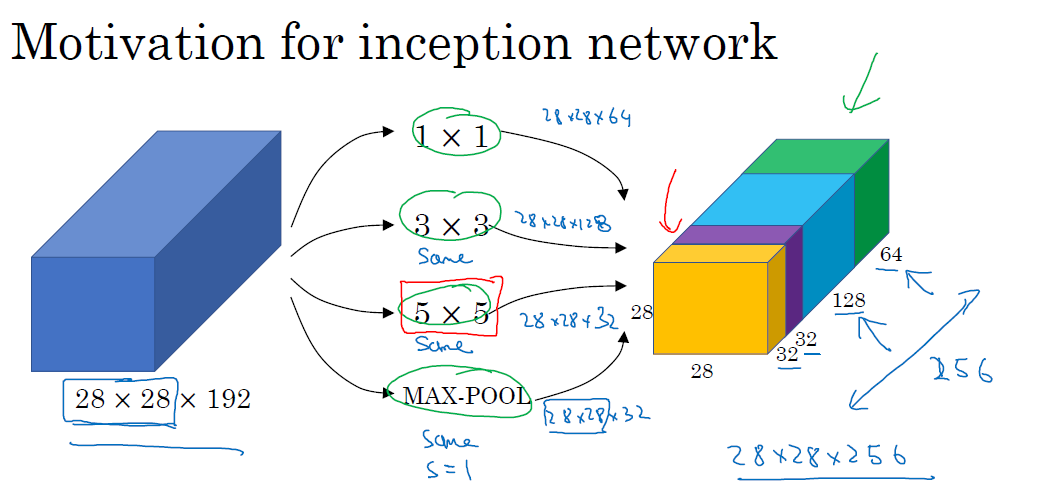
所有的conv layer和max-pool layer都用到了same padding，这样保证经过一个layer之后的维度不变，以便大家能够联结起来

但是inception network造成的问题就是计算量太大，比如我们现在来看看5*5这组filter的乘法的数目，一共输出是28*28*32个，每个输出所要求的乘法数目是5*5*192，所以全部乘起来之后是28*28*32*5*5*192=120M次

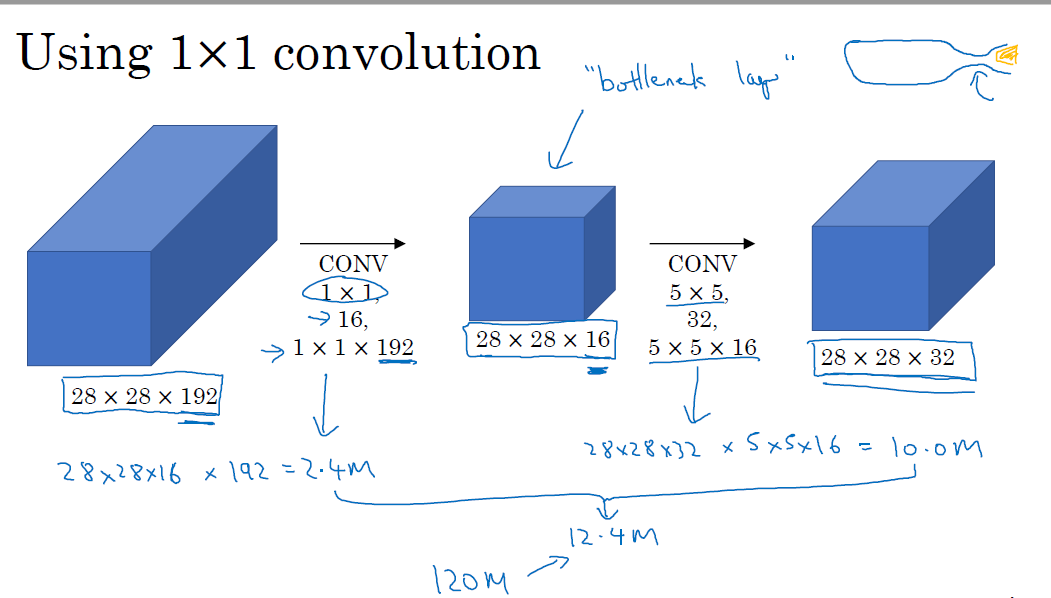
我们可以用上一节提到的1*1的conv 层进行计算次数的优化，用1*1的conv 层计算出一个 bottleneck layer（瓶颈层:和瓶颈一样，先变小，再变大），然后再计算乘法。具体来说是将28*28*192的图片先经过一个1*1的个数为16的层，变成28*28*16的层，然后再经过5*5的层，计算数量缩减为12.4M，如下图

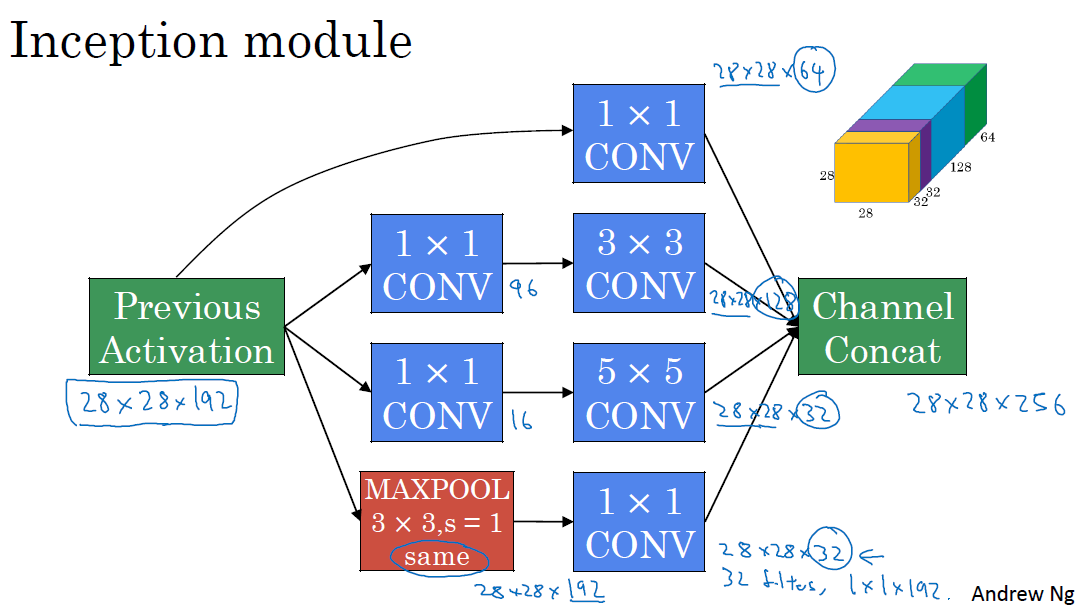
一个Inception module如下图所示，包含1*1的conv layer 和 3*3的conv layer(前面有一个1*1的bottleneck layer)和5*5的conv layer(前面有一个1*1的bottleneck layer)，以及一个3*3的max-pool layer（后面有一个1*1的layer用于减小通道数）

一个完整的inception network如下图所示，由多个inception module组成，中间还有一个side branch，用中间某一层的输出进行预测

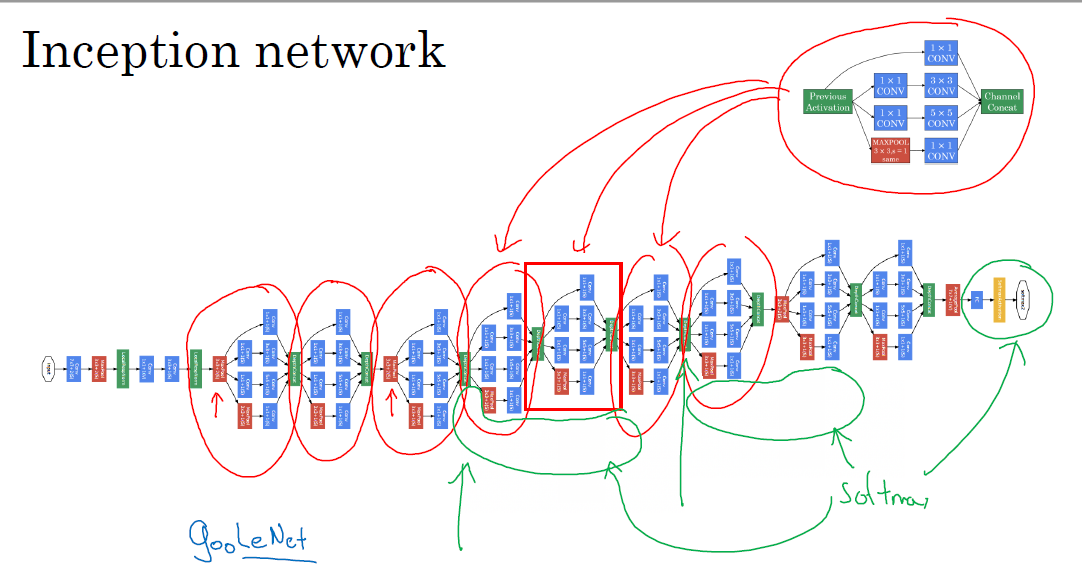
使用开源的深度学习实现

当你遇到一个想要去实现的网络的时候，从头开始动手实现是非常困难的，因为有很多调参之类的问题需要你去解决，那么你完全可以使用google 去搜索github上面的结果，比如你先想要实现ResNet， 你只需要在google上面搜索ResNet github，很容易就能找到一个结果，并且这些开源代码往往用了大量的原始数据进行训练，你只需要下下来进行迁移学习就行了

迁移学习

比如你现在想要是别的两只猫，分别叫做tigger和misty，但是你拥有的这两只猫的图片很少，所以你从网上下了一个在非常大数据集上面训练的模型(比如image net上训练过的模型)，然后你直接去掉输出层，把前面的所有层的参数都freeze住，对最后一层进行训练，就得到了你的猫分类器

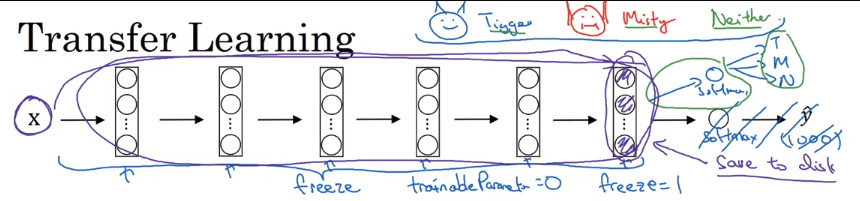
当然，如果你数据量大一些，你可以少冻住几层，多训练几层，这个freeze的方法，通常是将输入输进去，用原来的网络参数计算直到你要自己训练的那层，把这些数据存下来作为新网络的输入。后面网络参数的初始化可以直接用别人训练好的参数作为反向传播

除非你数据量非常大，不然你都不要完全重新训练网络

数据提升

数据提升主要有两种方法，一种是在图片内容上的变换，一种是色彩上的变换

内容上的变换主要有：镜像变换，随机裁剪，旋转，扭曲等等，如下图

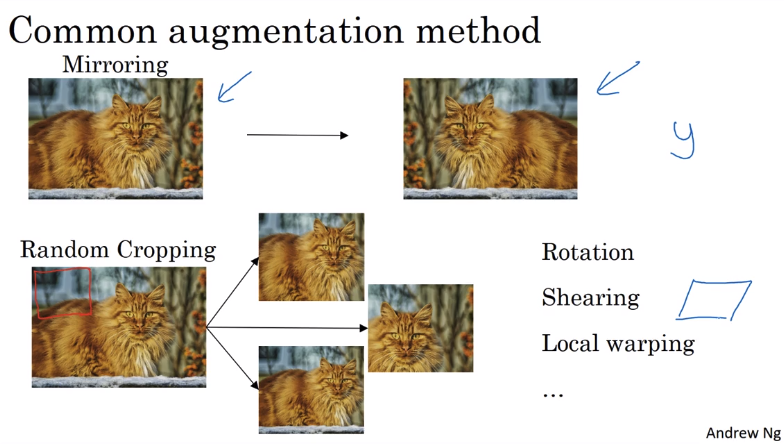
色彩上的变换主要是：增加或减少RGB色彩，比较高级的方法叫做PCA color augmentation，效果如图

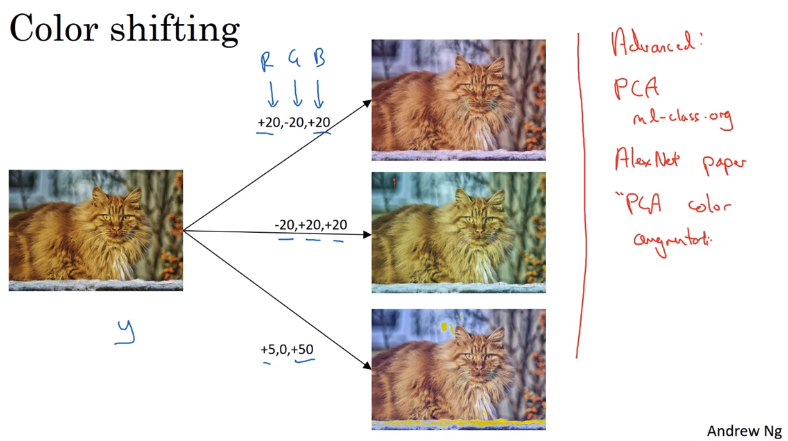
计算机视觉任务的经验

一般来说，数据越多，你所需要进行的手动修改的部分就越少，如图

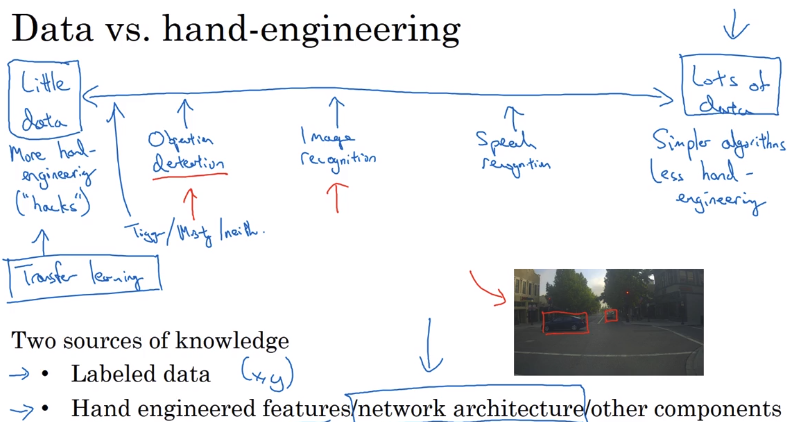
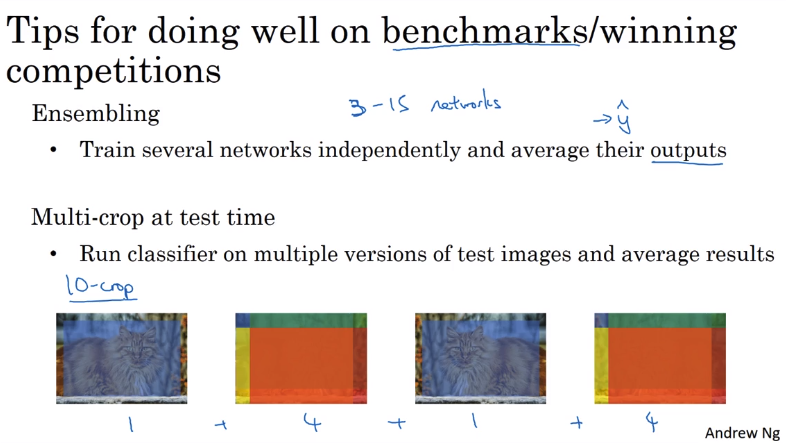
在标准数据集或者是竞赛当中有一些比较常用的方法：

  1. Ensembling：训练多个神经网络并平均输出
  2. 多种图片裁剪的数据提升方法：原图以及镜像图片的正中心，左上角，右上角，左下角，右下角图片，这个方法被称为crop-10，因为一共裁剪出10张

在使用开源框架的时候，通常可以：

  1. 用论文中提出的框架，因为一般计算机视觉任务有通用性
  2. 使用开源框架
  3. 使用pre-trained model并调整你模型中的参数

Keras tutorial

Keras更像是sklearn的过程，每一层的叠加都是可见的，然后最后compile一下model，fit model，然后evaluate model

具体来说，我们看看一个1层的卷积神经网络怎么实现的

先用Input函数得到输入，用ZeroPadding2d函数进行zero padding，用Conv2D进行卷积，用BatchNormalization进行批量正则化（每一层都进行正则化而不只是输入正则化），经过一个激活函数Activation(‘relu’)，用MaxPooling2D经过一个max pool，然后Flatten，然后用一个sigmoid函数得到输出，最后用model=Model(inputs=..., outputs=... ,name='...')建立模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def model(input_shape):
    # Define the input placeholder as a tensor with shape input_shape. Think of this as your input image!
    X_input = Input(input_shape)

    # Zero-Padding: pads the border of X_input with zeroes
    X = ZeroPadding2D((3, 3))(X_input)

    # CONV -> BN -> RELU Block applied to X
    X = Conv2D(32, (7, 7), strides = (1, 1), name = 'conv0')(X)
    X = BatchNormalization(axis = 3, name = 'bn0')(X)
    X = Activation('relu')(X)

    # MAXPOOL
    X = MaxPooling2D((2, 2), name='max_pool')(X)

    # FLATTEN X (means convert it to a vector) + FULLYCONNECTED
    X = Flatten()(X)
    X = Dense(1, activation='sigmoid', name='fc')(X)

    # Create model. This creates your Keras model instance, you'll use this instance to train/test the model.
    model = Model(inputs = X_input, outputs = X, name='HappyModel')

    return model

You have now built a function to describe your model. To train and test this model, there are four steps in Keras:

  1. Create the model by calling the function above
  2. Compile the model by calling model.compile(optimizer = "...", loss = "...", metrics = ["accuracy"])
  3. Train the model on train data by calling model.fit(x = ..., y = ..., epochs = ..., batch_size = ...)
  4. Test the model on test data by calling model.evaluate(x = ..., y = ...)

If you want to know more about model.compile(), model.fit(), model.evaluate() and their arguments, refer to the official Keras documentation.

现在建立模型的方法就是四步：

  1. 定义模型：happyModel = HappyModel(X_train.shape[1:])
  2. compile模型，定义其中的optimizer和loss以及metrics，happyModel.compile(optimizer = "Adam", loss = "binary_crossentropy", metrics = ["accuracy"])
  3. fit模型：happyModel.fit(x = X_train, y = Y_train, epochs = 5, batch_size = 16)，这里的batch-size选为16，一开始用了64，效果非常不好
  4. evaluate模型：preds = happyModel.evaluate(x = X_, y = ...)

keras当中比较有用的两个函数：

  1. 模型的每一层的参数个数：happyModel.summary()
  2. plot_model(happyModel, to_file='HappyModel.png')
    SVG(model_to_dot(happyModel).create(prog='dot', format='svg'))
    上面两行用于打印模型的结构

Keras to ResNet

首先导入一些需要用到的库

Keras是一个模型级的库，提供了快速构建深度学习网络的模块。Keras并不处理如张量乘法、卷积等底层操作。这些操作依赖于某种特定的、优化良好的张量操作库。Keras依赖于处理张量的库就称为“后端引擎”。Keras提供了三种后端引擎Theano/Tensorflow/CNTK，并将其函数统一封装，使得用户可以以同一个接口调用不同后端引擎的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from resnets_utils import *
from keras.initializers import glorot_uniform
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline

import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)   # 设置为训练/测试模式 ，分别是0/1

建立一个identity block

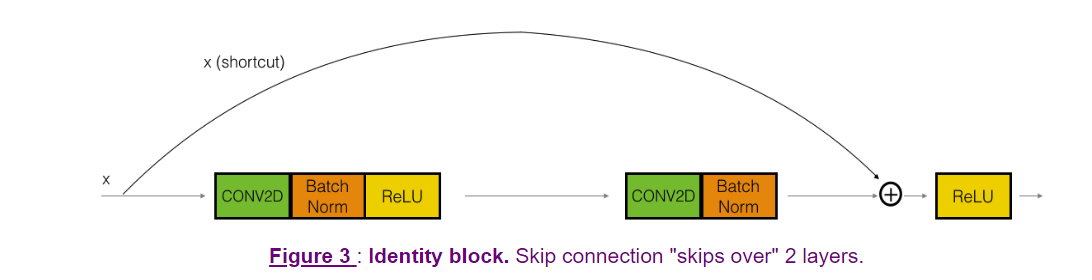
identity block是x[l]和 x[l+2]的size一样，就可以直接相加

用filters的list来存储三层的filter的个数，记录下一开始的X作为X_shortcut

然后开始主路的设计：先一个conv layer，然后一个BatchNormalization，axis=3，是除了3以外的所有维度都normalization，也可以写成axis=-1，然后是一个Activation(‘relu’)层

接下来的两层基本与第一层相同，只是filter的个数分别是F2,F3，filter的size中间那层是(f,f)

第三层结束之后得到的X加上一开始的X_shortcut，就是最终进入activation的值，这里的加法必须要用keras.layers.Add()()([x1,x2])或keras.layers.add([x1, x2])进行，直接用加号会出错

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# GRADED FUNCTION: identity_block

def identity_block(X, f, filters, stage, block):
    """
    Implementation of the identity block as defined in Figure 3
    
    Arguments:
    X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
    f -- integer, specifying the shape of the middle CONV's window for the main path
    filters -- python list of integers, defining the number of filters in the CONV layers of the main path
    stage -- integer, used to name the layers, depending on their position in the network
    block -- string/character, used to name the layers, depending on their position in the network
    
    Returns:
    X -- output of the identity block, tensor of shape (n_H, n_W, n_C)
    """
    
    # defining name basis
    conv_name_base = 'res' + str(stage) + block + '_branch'
    bn_name_base = 'bn' + str(stage) + block + '_branch'
    
    # Retrieve Filters
    F1, F2, F3 = filters
    
    # Save the input value. You'll need this later to add back to the main path. 
    X_shortcut = X
    
    # First component of main path
    X = Conv2D(filters = F1, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
    X = Activation('relu')(X)
    
    ### START CODE HERE ###

    # Second component of main path (≈3 lines)
    X = Conv2D(filters = F2, kernel_size = (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
    X = Activation('relu')(X)

    # Third component of main path (≈2 lines)
    X = Conv2D(filters = F3, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)

    # Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
    X = Add()([X, X_shortcut])  # added = keras.layers.Add()([x1, x2])  ## equivalent to added = keras.layers.add([x1, x2])
    X = Activation('relu')(X)

    ### END CODE HERE ###
    
    return X

然后开始tensorflow测试一下identity block，定义一个A_prev的placeholder，类型是float，shape=[3,4,4,6]，X设为一个[3,4,4,6]的随机矩阵，用A_prev建立一个identity block，三层filter的个数是2,4,6，第二层的filter的形状是2*2，然后用sess run 变量初始化，接着run一下这个identity block，feed_dict数据是A_prev:x,K.learning_phase(): 0用于转换为训练模式

1
2
3
4
5
6
7
8
9
10
tf.reset_default_graph()

with tf.Session() as test:
    np.random.seed(1)
    A_prev = tf.placeholder("float", [3, 4, 4, 6])
    X = np.random.randn(3, 4, 4, 6)
    A = identity_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
    test.run(tf.global_variables_initializer())
    out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
    print("out = " + str(out[0][1][1][0]))

建立一个convlutional block

convlutional block就是shortcut不是直接加到a[l+2]上面的，而是经过了一个conv layer和batch norm之后加的

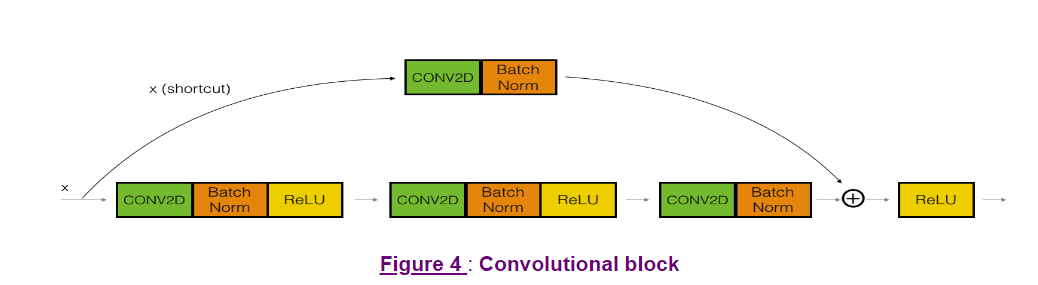
与建立identity layer的方法类似，记录X为X_shortcut，这里的shortcut到后面是要经过运算的，不是直接加的

每个conv layer 有一个kernel的initializer， kernel_initializer = glorot_uniform(seed=0)就是常用的Xavier 初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# GRADED FUNCTION: convolutional_block

def convolutional_block(X, f, filters, stage, block, s = 2):
    """
    Implementation of the convolutional block as defined in Figure 4
    
    Arguments:
    X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
    f -- integer, specifying the shape of the middle CONV's window for the main path
    filters -- python list of integers, defining the number of filters in the CONV layers of the main path
    stage -- integer, used to name the layers, depending on their position in the network
    block -- string/character, used to name the layers, depending on their position in the network
    s -- Integer, specifying the stride to be used
    
    Returns:
    X -- output of the convolutional block, tensor of shape (n_H, n_W, n_C)
    """
    
    # defining name basis
    conv_name_base = 'res' + str(stage) + block + '_branch'
    bn_name_base = 'bn' + str(stage) + block + '_branch'
    
    # Retrieve Filters
    F1, F2, F3 = filters
    
    # Save the input value
    X_shortcut = X


    ##### MAIN PATH #####
    # First component of main path 
    X = Conv2D(F1, (1, 1), strides = (s,s),padding='valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
    X = Activation('relu')(X)
    
    ### START CODE HERE ###

    # Second component of main path (≈3 lines)
    X = Conv2D(F2, (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
    X = Activation('relu')(X)

    # Third component of main path (≈2 lines)
    X = Conv2D(F3, (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)

    ##### SHORTCUT PATH #### (≈2 lines)
    X_shortcut = Conv2D(F3, (1, 1), strides = (s,s), padding = 'valid', name = conv_name_base + '1', kernel_initializer = glorot_uniform(seed=0))(X_shortcut)
    X_shortcut = BatchNormalization(axis = 3, name = bn_name_base + '1')(X_shortcut)

    # Final step: Add shortcut value to main path, and pass it through a RELU activation (≈2 lines)
    X = Add()([X, X_shortcut])
    X = Activation('relu')(X)

    ### END CODE HERE ###
    
    return X

同样来测试一下我们建立的convolutional block

1
2
3
4
5
6
7
8
9
10
tf.reset_default_graph()

with tf.Session() as test:
    np.random.seed(1)
    A_prev = tf.placeholder("float", [3, 4, 4, 6])
    X = np.random.randn(3, 4, 4, 6)
    A = convolutional_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
    test.run(tf.global_variables_initializer())
    out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
    print("out = " + str(out[0][1][1][0]))

建立一个50层的ResNet

结构如下图所示，分为5个stage，其中的conv block就是我们在上面建立的convolutional block，其中的ID block就是我们上面建立的identity block

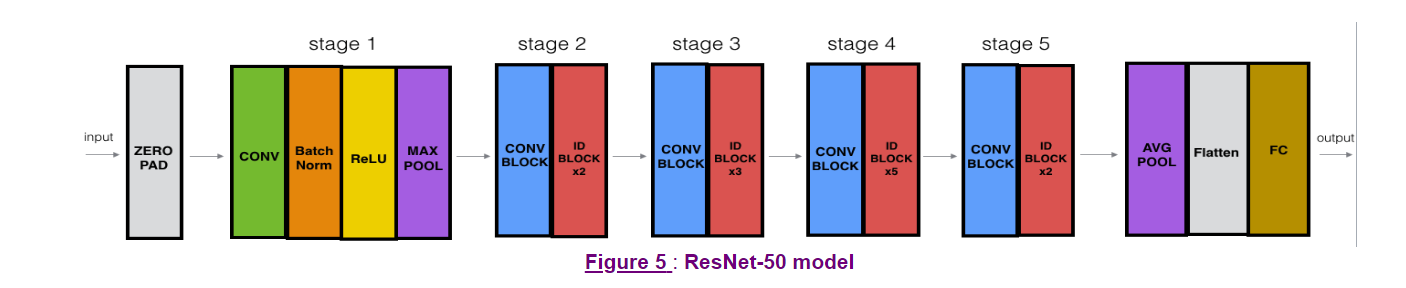
我们先给一个大小就可以定义一个输入的tensor，用Input方法实现

先进入一个zero padding，然后一个conv layer，batch norm，relu，max pool，接下来就是一大堆的block，然后接一个AvgPool，flatten一下，接一个FC layer，就得到了输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# GRADED FUNCTION: ResNet50

def ResNet50(input_shape = (64, 64, 3), classes = 6):
    """
    Implementation of the popular ResNet50 the following architecture:
    CONV2D -> BATCHNORM -> RELU -> MAXPOOL -> CONVBLOCK -> IDBLOCK*2 -> CONVBLOCK -> IDBLOCK*3
    -> CONVBLOCK -> IDBLOCK*5 -> CONVBLOCK -> IDBLOCK*2 -> AVGPOOL -> TOPLAYER

    Arguments:
    input_shape -- shape of the images of the dataset
    classes -- integer, number of classes

    Returns:
    model -- a Model() instance in Keras
    """
    
    # Define the input as a tensor with shape input_shape
    X_input = Input(input_shape)

    
    # Zero-Padding
    X = ZeroPadding2D((3, 3))(X_input)
    
    # Stage 1
    X = Conv2D(64, (7, 7), strides = (2, 2), name = 'conv1', kernel_initializer = glorot_uniform(seed=0))(X)
    X = BatchNormalization(axis = 3, name = 'bn_conv1')(X)
    X = Activation('relu')(X)
    X = MaxPooling2D((3, 3), strides=(2, 2))(X)

    # Stage 2
    X = convolutional_block(X, f = 3, filters = [64, 64, 256], stage = 2, block='a', s = 1)
    X = identity_block(X, 3, [64, 64, 256], stage=2, block='b')
    X = identity_block(X, 3, [64, 64, 256], stage=2, block='c')

    ### START CODE HERE ###

    # Stage 3 (≈4 lines)
    X = convolutional_block(X, f = 3, filters = [128, 128, 512], stage = 3, block='a', s = 2)
    X = identity_block(X, 3, [128, 128, 512], stage=3, block='b')
    X = identity_block(X, 3, [128, 128, 512], stage=3, block='c')
    X = identity_block(X, 3, [128, 128, 512], stage=3, block='d')

    # Stage 4 (≈6 lines)
    X = convolutional_block(X, f = 3, filters = [256, 256, 1024], stage = 4, block='a', s = 2)
    X = identity_block(X, 3, [256, 256, 1024], stage=4, block='b')
    X = identity_block(X, 3, [256, 256, 1024], stage=4, block='c')
    X = identity_block(X, 3, [256, 256, 1024], stage=4, block='d')
    X = identity_block(X, 3, [256, 256, 1024], stage=4, block='e')
    X = identity_block(X, 3, [256, 256, 1024], stage=4, block='f')

    # Stage 5 (≈3 lines)
    X = convolutional_block(X, f = 3, filters = [512, 512, 2048], stage = 5, block='a', s = 2)
    X = identity_block(X, 3, [512, 512, 2048], stage=5, block='b')
    X = identity_block(X, 3, [512, 512, 2048], stage=5, block='c')

    # AVGPOOL (≈1 line). Use "X = AveragePooling2D(...)(X)"
    X = AveragePooling2D(pool_size=(2, 2))(X)
    
    ### END CODE HERE ###

    # output layer
    X = Flatten()(X)
    X = Dense(classes, activation='softmax', name='fc' + str(classes), kernel_initializer = glorot_uniform(seed=0))(X)
    
    
    # Create model
    model = Model(inputs = X_input, outputs = X, name='ResNet50')

    return model

接下来定义我们的model

1
model = ResNet50(input_shape = (64, 64, 3), classes = 6)

然后compile model，指定optimizer和loss以及metric

1
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

导入数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.

# Convert training and test labels to one hot matrices
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T

# number of training examples = 1080
# number of test examples = 120
# X_train shape: (1080, 64, 64, 3)
# Y_train shape: (1080, 6)
# X_test shape: (120, 64, 64, 3)
# Y_test shape: (120, 6)

1080张64*64的三通道图片，测试时120张64*64的三通道图片

接下来fit model

1
model.fit(X_train, Y_train, epochs = 20, batch_size = 32)

最后evaluate模型

1
2
3
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))

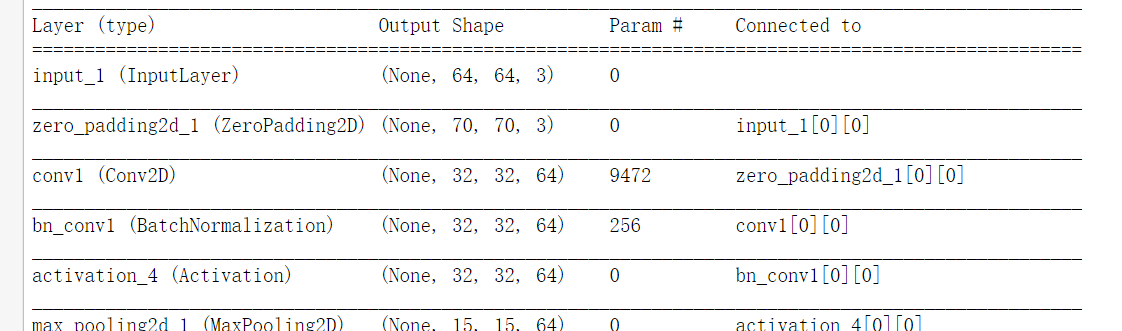
同样summary()和plot_model看看参数以及网络结构

1
2
3
model.summary()
plot_model(model, to_file='model.png')
SVG(model_to_dot(model).create(prog='dot', format='svg'))

Week Three 检测算法

目标定位

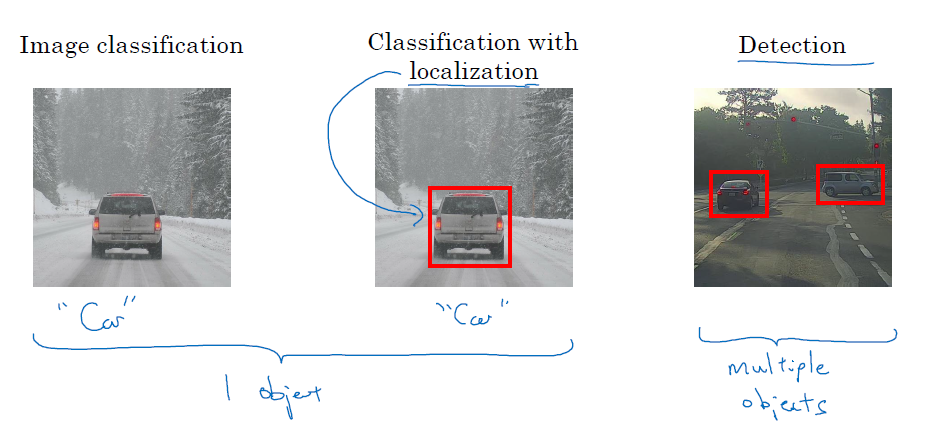
目标检测主要有两类任务，一类是image classification 和 classification with localization，往往只有一个目标需要标记，另一类是detection，往往有多个目标需要标记

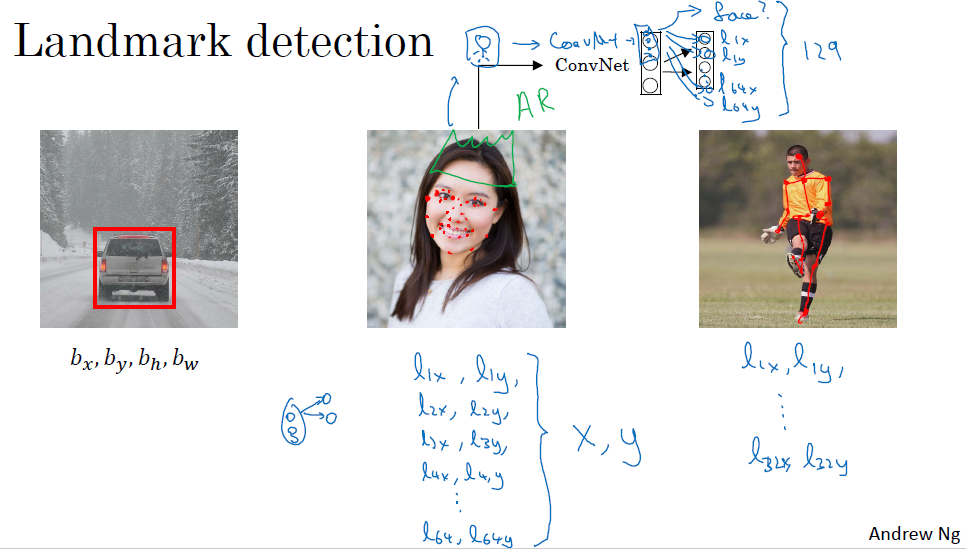
当你需要标记目标位置的时候，你的神经网络的输出不仅是一个softmax的概率值，还有图像中心点的x，y坐标以及红框的宽和高的值，假设我们现在检测三类目标，分别是行人，汽车，摩托车，以及三类都没有的纯背景的情况，那么你的y应该设置为
$$
y=\begin{bmatrix}P_c \b_x \b_y \b_h \b_w \c_1 \c_2 \c_3 \end{bmatrix}
$$

其中$P_c$表示的是图中有无目标，如果有目标那么就要定位$b_x,b_y,b_h,b_w$，以及他们的分类$c_1,c_2,c_3$

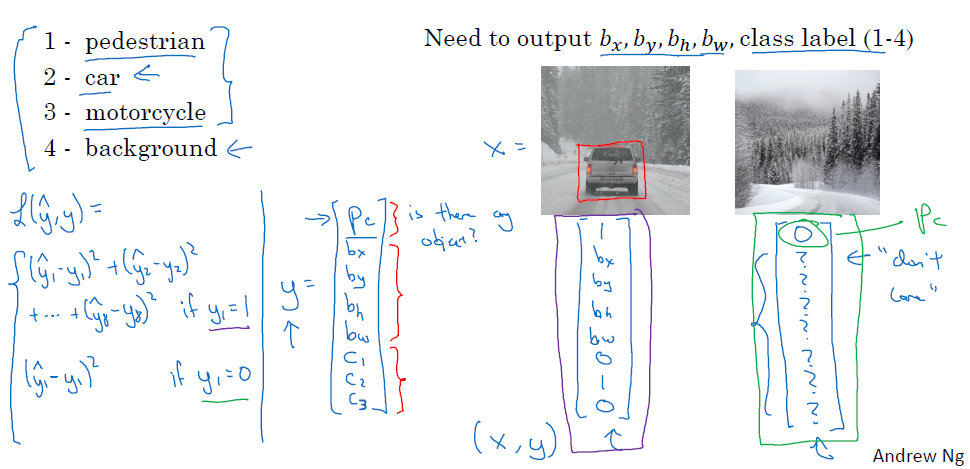
当$P_c = 1$的时候，y的所有参数都是需要关心的

当$P_c = 0$，除了$P_c $以外的其余参数都不用关心，图中用问号表示

损失函数可以表示为
$$
L(\hat y,y)=\left{\begin{matrix}
(\hat y_1,y_1)^2+\ldots+(\hat y_8,y_8)^2 & if & y=1\
(\hat y_1,y_1)^2 & if & y=0
\end{matrix}\right.
$$

特征点检测

当你检测一个人或者是一个姿势的时候，你可能需要的不是像检测汽车那样只要一个中心点，你可能需要很多个点来检测人脸的五官，或者不同的点来检测一个人的姿势，此时你的y就有很多个点

利用滑动窗口进行目标检测

用一个正方形框在图像上以一定步长滑动，每次检测框内的图像，这就是滑动窗口的含义，用不同大小的框可以多次进行

但是滑动窗口的计算成本非常大，如果你的步长选的比较小（精度比较高），那么你要输入系统的图片非常多，计算量就非常大

使用卷积实现滑动窗口

使用卷积实现滑动窗口，首先要看看如何把FC层转换为卷积层，在本来应该flatten的地方，再用一组f大小与原图相等的filter，将它变成1*1的volume，然后反复使用1*1的filter，直到最后大小等于1*1*4

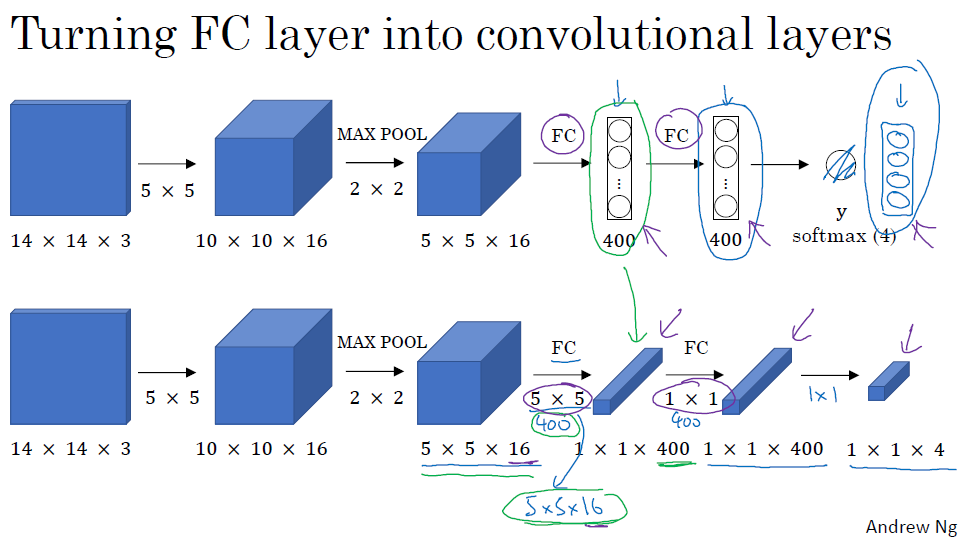
同样，在滑动窗口的过程中，有很多的卷积步骤是重复的，因此我们可以使用卷积来避免每个滑动窗口都经历整个卷积神经网络

获得更加精确的边界框

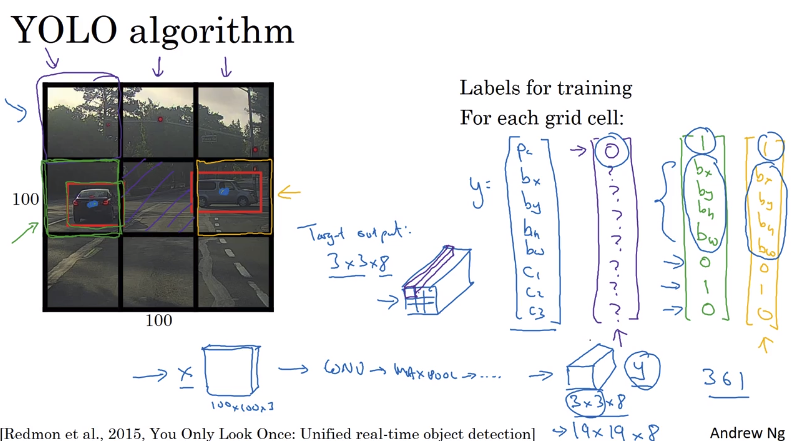
YOLO(You Only Look Once)算法是一个很好用的目标检测算法，先讲图片分割成很多个小的矩形，每个矩形中间如果有某个目标对象的中心点，那么这个方框的Y的第一个值$P_c$就为1，否则为0，最后得到一个3*3*8的volume，这个volume就是预测的结果，因为这个算法使用了卷积的方法，因此速度很快

我们来看个例子，比如下图，原图是100*100的大小，我们划分成3*3的格子，绿色和橙色格子有目标，找出中心点，然后标记出方框，绿色块的y值如右边的绿色y所示，橙色如橙色标识的y所示，其余的都是紫色标记

通常我们划分的块会更多一些，以便更加精确地定位图像

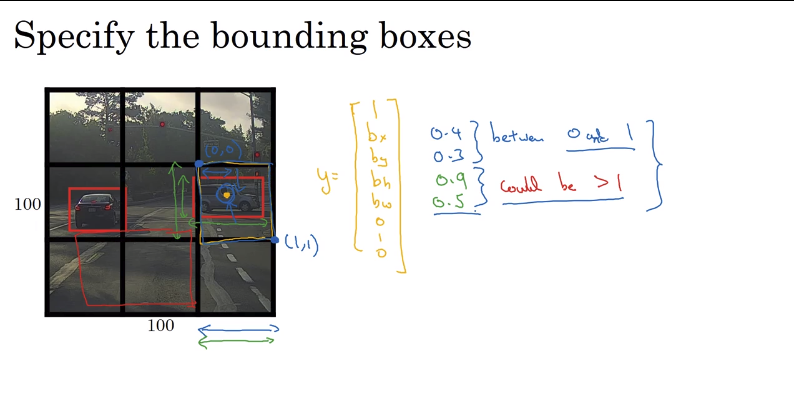
边框的标记方法是给出中心点的坐标x，y，已经图像的高度h和宽度w，因为我们对每个小方块的坐标定义为左上角是(0,0)，右下角是(1,1)，所以x,y一定是在0到1之间的值，但是目标的大小可能超出一个方块，所以h和w可以是大于0的任何值（当然也可以大于1），如下图

交并比（intersection over union）

交并比：一个方框与真实结果的交集与其并集的比，用于评价目标检测算法的精度

最好情况的交并比是1，一般来说，如果你的交并比（IoU）>=0.5，就认为你的检测是正确的

非最大值抑制(Non-max Suppression)

加入你在下图中检测汽车，你把图片分成了19*19大小的网格，两辆车的中心分别是绿色点和黄色点，理论上来说它们各自的中心点应该只会被标记一次，但是你在运行网络的时候，每一个网格都是独立运行的，所以旁边的网格可能也会认为自己就在图片中心，同一个目标可能会被标记好多次，因此引入非最大值抑制的策略来保证每个目标只被标记一次

假设我们现在已经得到了很多个框，你需要去找到哪个框是真的有效的，如下图

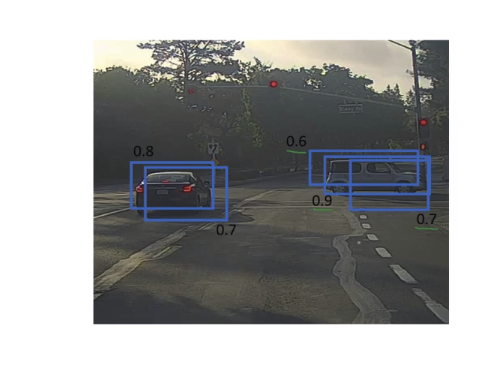
具体做法如下：

  1. 首先，你将那些概率值都低于0.6的框给删除
  2. 只要这里还剩任何框：选择现在概率最大的框最为结果，删除任何与这个结果IoU大于等于0.5的盒子
  3. 只要还有框没有标记就跳到第二步

Anchor Box

Anchor Box是用来当你需要检测多个目标的时候，你先给几个预先给定的anchor box，将结果的y联合起来

比如你现在检测行人和车辆，行人的车辆应该是高长的，车辆的扁宽的，本来y是8维的，然后现在连接起来就有16维

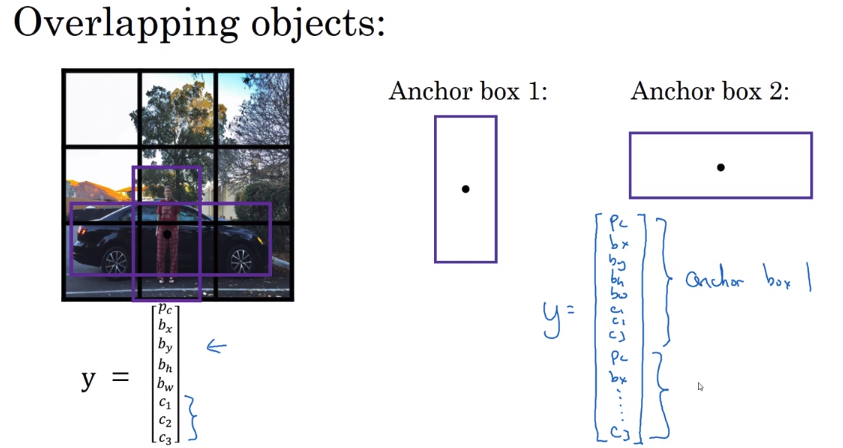
然后我们将两个anchor box 和 我们之前圈出来的框计算IoU，图像将被分到高IoU的部分

YOLO算法的完整描述

如果你在进行一个定位行人，汽车，摩托车的YOLO算法，如下图，先将图片分成3*3的网格，对每一个网格进行检测，现在设定了2个anchor box，那么最终的输出是3*3*16的结果

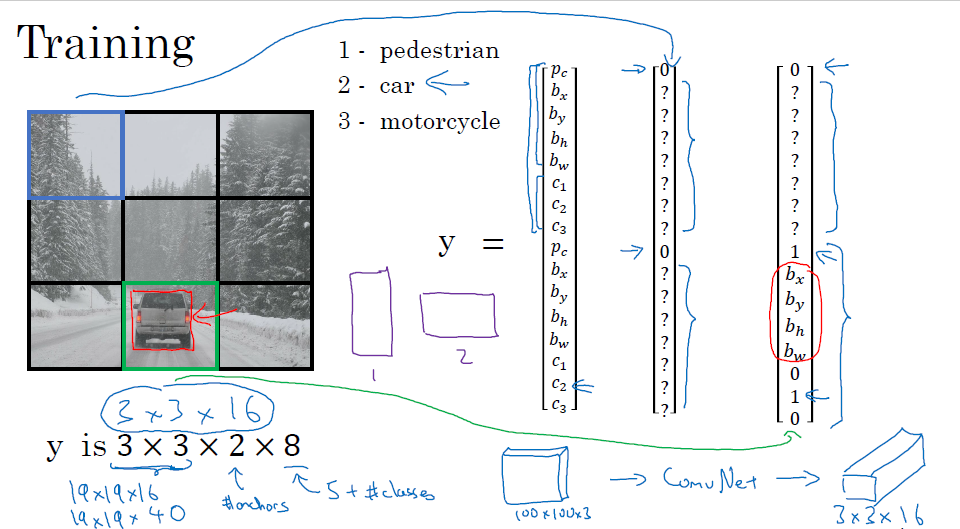
我们来看看如何做预测，如下图，我们将最终的结果全为$P_c$全为0的分类成背景，为1的部分去找对应的c的分类

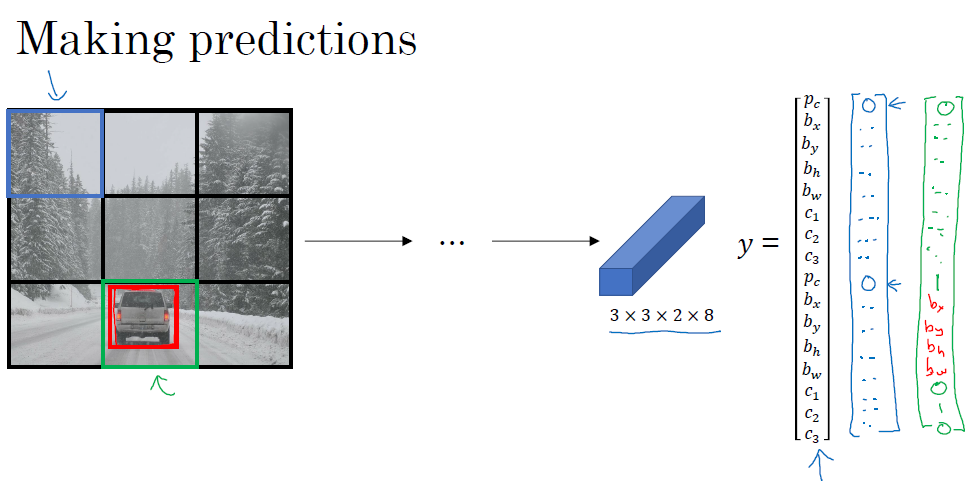
我们再来看看如何使用non-max suppress，先从图中移除那些概率很低的框，然后分别对三个类别（行人，汽车，摩托车）进行non-max suppress得到最终的预测

Week four

人脸识别的术语

人脸识别任务大致分为两类，分别是face verification 和 face recognition：

  • face verification：指的是给一张图片，判定是否是你要找的那个人，是一个二分类的问题
  • face recognition：是给一张图片，判定他是谁，是一个多分类问题

单样本学习问题(one shot learning)

通常识别任务要求在只有一张图片的情况下进行识别，但是从传统来说，只有一个训练样本的效果是很差的

解决的办法就是，学习出一个相似性函数，给定两张图片，如果两张图片的相似度比较大（距离比较小），那么两张图片就是同一个人。我们设定一个阈值，如果小于这个阈值，我们认为是同一个人，如果大于这个阈值，我们认为是不同的人。这样，即使有新的人加入这个系统，你的系统依然可以进行判断

孪生网络（Siamese Network）

普通的卷积神经网络是先经过几个卷基层，然后经过一个FC layer，最后一个softmax进行判别，我们在这里删除最后的softmax层，将最后的FC层的输出作为一张图片的编码

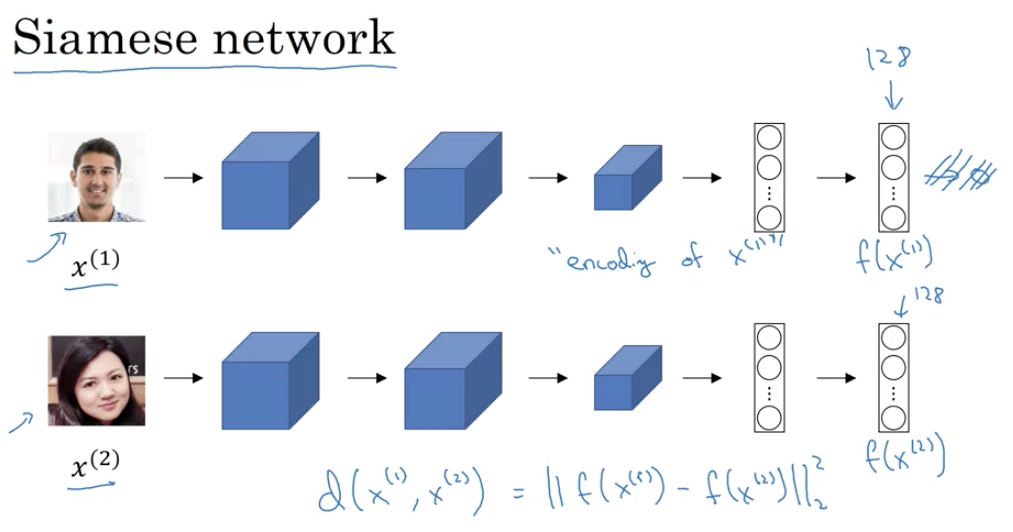
将这些输出的编码作为结果，计算距离，并使得同一个人的不同图片距离小，不同人的图片距离大，以此作为目标进行反向传播，具体的loss函数被称为triple loss function

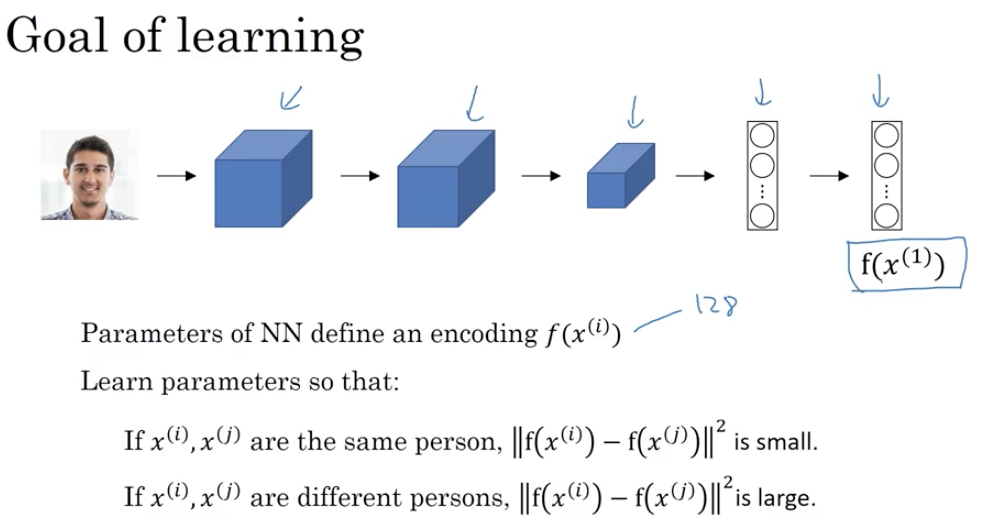
三重损失函数（triple loss function）

我们每次进行训练的图片应该有三张：Anchor，Positive，Negative，分别代表原始图片，同一个人的图片，另一个人的图片，计算Anchor和Positive以及Negative之间的距离，记作d(A,P)和d(A,N)，计算方法是通过神经网络给出的编码，计算欧式距离，要求同一个人的不同图片距离小(d(A,P)小)，不同人的图片距离大（d(A,N)大），并且他们之间不能是基本相同的大小，因为那样对于分类器来说是比较难区分的，我们把差距超过一定范围$\alpha$的才能称为不同人，如下图所示

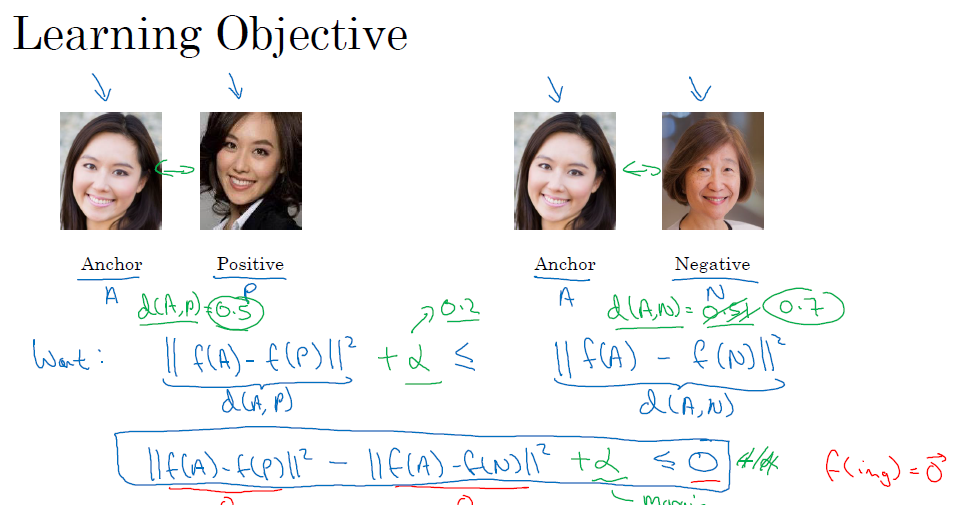
那么损失函数可以是上图中的右式移到左边，那么要求这个损失小于等于0，那么我们取Loss为
$$
L(A,P.N)=max(||f(A)-f(N)||^2-||f(A)-f(N)||^2+\alpha,:0)
$$
那么代价函数就是
$$
J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})
$$
训练的数据要足够的大，一个人应该有好几张图片，如果只有一张图片是很难训练的

如何选择APN也是有要求的，如果你A,P,N都随机选择，那么两张不同人的图片距离一般来说是肯定大于一个人的两张图片的，所以我们应该选那些尽可能接近的距离值去训练，也就是d(A,P)和d(A,N)要尽量靠近一些

在深度学习中，这些系统的名字一般选择为xxNet或者是Deepxx，比如这里的FaceNet和之前提到的DeepFace

二分类的人脸识别

另一种进行人脸识别的方法是二分类，当你有一个新的图片需要分类的时候，将它输入一个已经训练好的卷积神经网络，得到一个编码，与系统中另一张图片的编码经过一个logistic单元，最终的$\hat y$如果为1，证明图片来自同一个人，否则来自于不同人

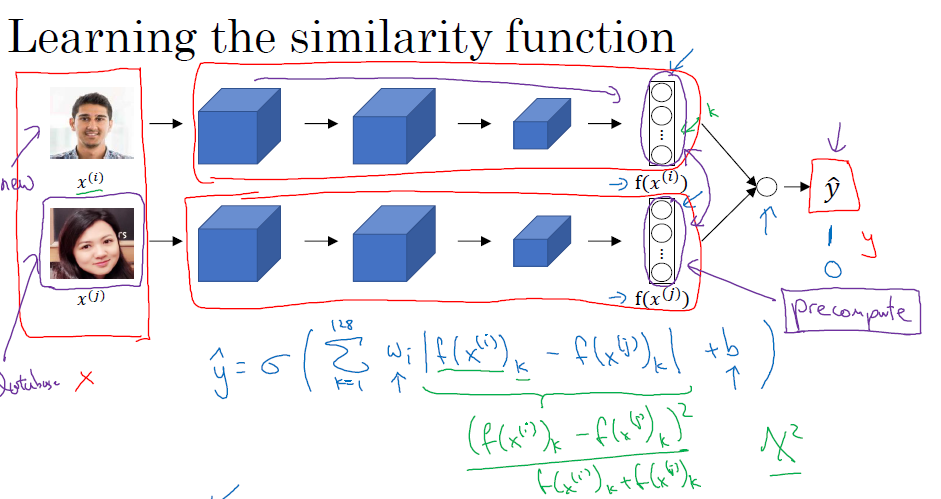
这里有个节省计算能力的好办法，就是系统中的图片，你应该全部先通过卷及网络算出编码，直接存储编码，这样每次你只需要将新图片经过这个神经网络得到编码，再做一个logistic计算就可以了

风格迁移

什么是风格迁移

如下图，我们将原图(Content)称为C，风格图（Style）称为S，生成的图片（Gnerated image）称为G

深度卷积神经网络究竟学的是什么

卷积神经网络的前面层，是一些图片的边缘信息，越到后面的层，信息越丰富

风格迁移的代价函数

我们用C表示Content这张图，用S表示Style这张图，G代表Generated image，要求定义的代价函数在最小化时使用梯度下降：
$$
J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)
$$
风格迁移的过程：

  1. 随机初始化G
  2. 进行梯度下降，是的cost function变小，然后输出的图像和C和S的混合越来越像

Content cost function

你用第$l$层的卷积网络去计算你的content cost function，这个层数不能太靠前（前面全是边缘信息），也不能太靠后（太靠后已经是完整的图片了），你的Content cost function只需要计算第$l$层的Content和Generated 的输出的相似度，我们在这里使用L-2范数
$$
J_{content}(C,G)=||a^{l}-a^{l}||^2
$$

Style cost function

要定义S和G的风格相似度，我们要来看看如何定义风格的相似，这里引入一个Style matrix的概念，用于定义不同层之间的像素值的乘积和，用$a_{i,j,k}^{[l]}$表示第$l$层的一个像素点，用$G^{[l]}$表示第l层的Style Matrix
$$
G^{l}{kk\prime} = \sum{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{ijk}^{l}a_{ijk\prime}^{l} \
G^{l}{kk\prime} = \sum{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{ijk}^{l}a_{ijk\prime}^{l} \
$$
第l层的style cost function就用这两个style function的相似度来计算
$$
\begin{array}{rcl}
J_{style}^{[l]}(S,G) &=& \frac{1}{(…)}||G^{l}-G^{l}||^2 \
&=& \frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2}\sum_k\sum_{k{\prime}}(G^{l}{kk\prime}-G^{l}{kk\prime})
\end{array}
$$
通常一层的效果不够好，因此我们多用几层
$$
J_{style}(S,G)=\sum_l\lambda^{[l]}J_{style}^{[l]}(S,G)
$$
最终的J就是把content和style的J加起来
$$
J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)
$$

1D和3D数据的卷积

1D数据通常是信号数据，你用的卷积核应该也是1D的，比如你一开始是14*1的信号，卷积16个5*1的filter，变成

3D图像通常有CT图，视频之类的，有长，宽，深度三个维度，