这篇博文主要讲的是关于deeplearning.ai的第二门课程的内容,《Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization》
Week one
设置训练,验证,测试集
设置神经网络时,有很多的值需要你自己设置,比如隐藏层的数量,隐藏点的个数,学习率,激活函数的类型等等……
数据通常被分为三部分:训练集,hold-out交叉验证集(或者成为开发集dev),测试集。分布如下图所示:
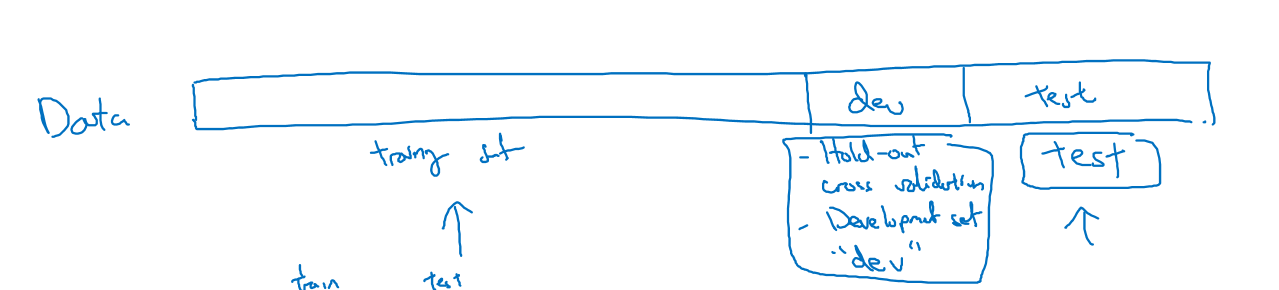
多年前,数据较少:70%的训练数据和30%的测试数据,或者60%训练数据,验证集和测试集各占20%
但现在数据越来越多,100w的总数据,验证集和测试集可能都只需要1w个就行了,剩下的98w数据都可以用于训练,比例为98/1/1
数据更多的时候,可能开发集和测试集所占的比例更小
数据不平衡
训练集,开发集,测试集的数据分布不同,比如图片识别中,两边的数据来源不同(一边是高清图片,一边是模糊图片),这时候只需要保证开发集和测试集在同一个分布即可。
偏差方差
深度学习中有一个问题叫做“偏差-方差困境”,要在偏差和方差之间权衡
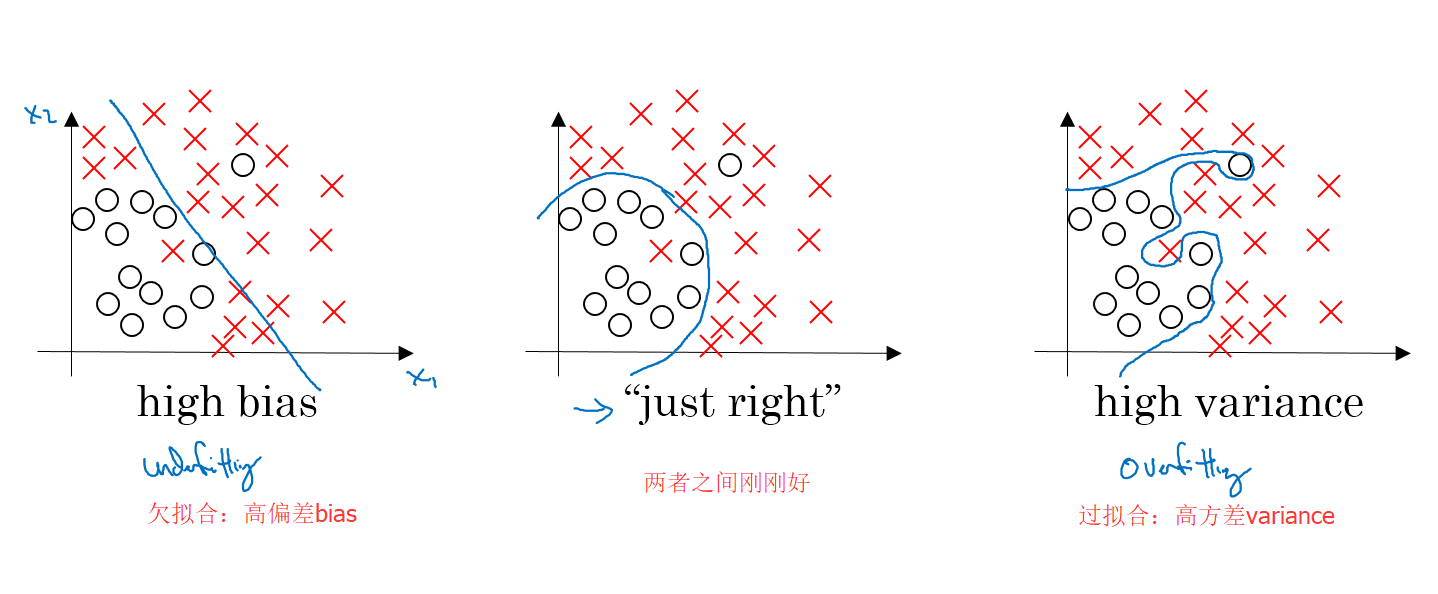
如何判断是高方差还是高偏差
往往通过训练集误差和开发集误差的对比来进行判断:
- 训练集误差小,开发集误差大,证明过拟合了,高方差
- 训练集误差大,开发集误差约等于训练集误差,证明欠拟合,高偏差
- 训练集误差大,开发集误差远大于训练集,证明高偏差且高方差,这是因为在某些数据上过拟合,而在大部分数据上欠拟合
- 训练集误差小,开发集误差也很小,这就是最理想的状态
下面这个分类猫的例子比较直观解释了上面四种情况,注意,此时所谓的大小是因为我们设置的贝叶斯先验错误为0%,所以认为1%小,15%大。如果贝叶斯先验概率不是0%而是15%,那么15%的错误率也是很小的了。并且此时要求训练集和开发集的数据分布是相同的(如果一个是高质量数据,一个是低质量数据,那么两个本来错误率就不一样)。

机器学习的基本准则
训练好模型之后:
- 首先询问,是否存在高偏差(在训练集上面的表现),如果存在,那么你可以尝试使用更大的网络(更多层和更多隐藏点),或者尝试训练更多的迭代次数。尝试多种方法,直到将偏差减小到一个可以接受的范围。
- 再看看是否有较高的方差(在开发集上面的表现),如果存在,那么比较好的办法就是增加训练数据,或者是正则化
正则化
如果发现过拟合,那么就是方差过大,首先应该尝试的方法就是正则化
以逻辑回归为例,为了最小化代价函数$J(W,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)})$,我们在后面加上一个W的范数,常用的范数为二范数,代价函数变为:
$J(W,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)})+\frac{\lambda}{2m}||w||^{2}_{2}$
其中的$\lambda$是正则化参数,$||w||^{2}{2}$称为w的二范数,$||w||^{2}{2}=\sum_{j=1}^{n_{x}}w_j^2=w^Tw$
为什么只对w正则化而忽略b呢,这是因为在过拟合的情况下,w的维度非常大,而b只有一个参数,影响相对于w来说可以忽略
偶尔也用一范数,但很少用,具体的逻辑回归的正则化方法如下
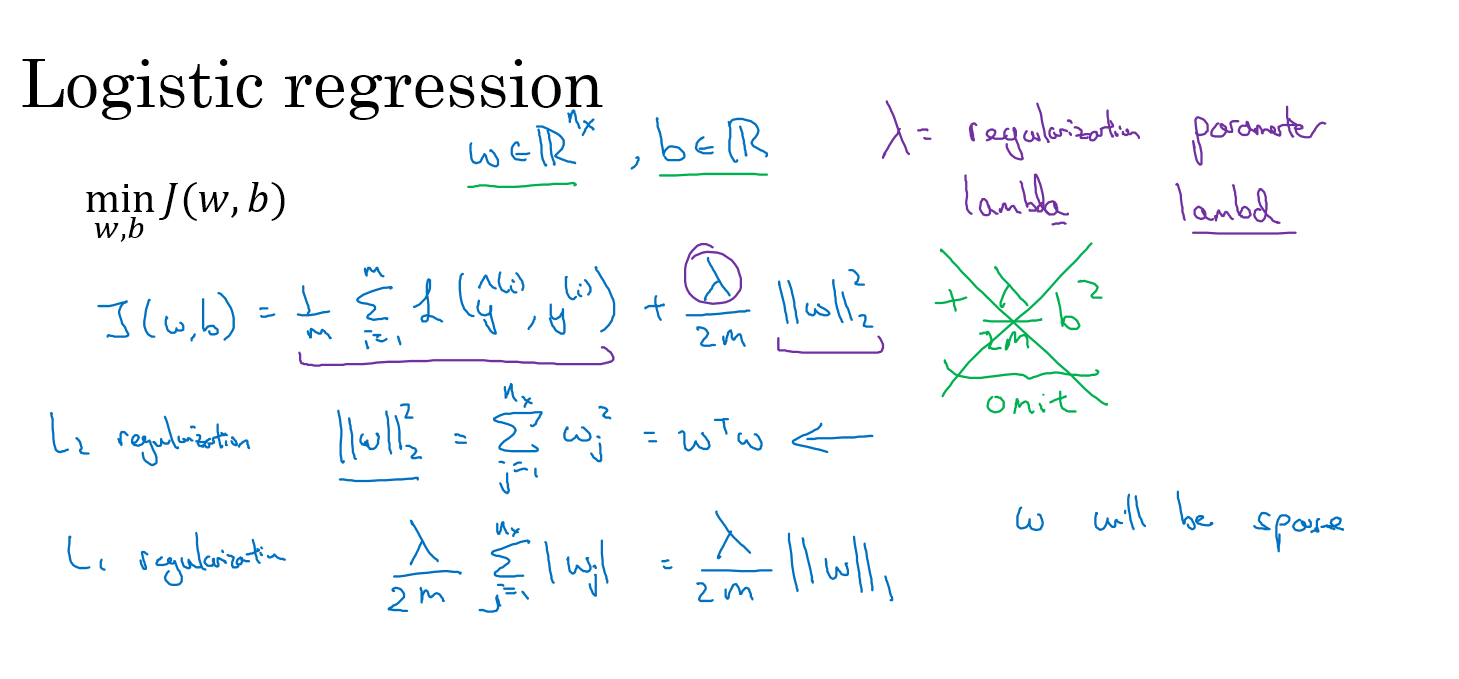
神经网络的正则化
神经网路的正则化的方法和逻辑回归基本一样,只是w的二范数成了w矩阵的元素平方和,这个值被称为Frobenius norm(弗罗贝尼乌斯范数)
在反向传播的时候,反向传播的$dw^{[l]}$就成了原本的反向传播的值(下图中间绿色方框行,由代价函数J求导得到),加上$\frac{\lambda}{m}w^{[l]}$,w的更新公式就成了这样:
$w^{[l]}=(1-\frac{\alpha\lambda}{m})w^{[l]}-\alpha(原本的反向传播值)$
所以正则化之后,每次更新相当于只是在原本的w前面乘以一个略小于1的值$1-\frac{\alpha\lambda}{m}$,再减去原本的反向传播的值,因此神经网络的正则化又被称之为权重衰减

为什么正则化可以消除过拟合
如图,如果过拟合,我们在加入正则化之后,如果把$\lambda$设置的非常大,那么为了是代价函数最小,w必须非常小,那么w的很多值就为0了,多层神经网络看上去就像是一个简单神经网路一样

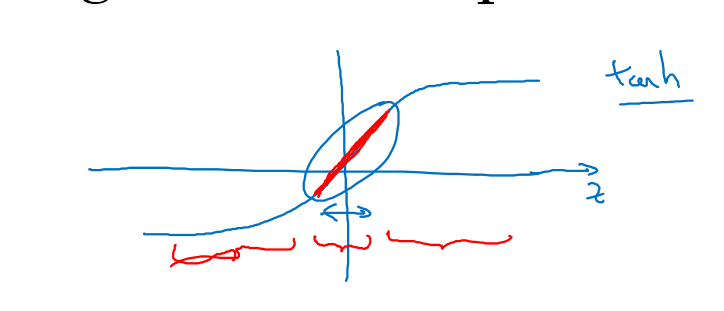
另一个直观解释是当你使用tanh之类的激活函数的时候,当$\lambda$非常大的时候,那么w非常小,因此z也非常小,经过激活函数变化之后的a也非常小,因此a值只能在0附近变化,这一段tanh函数基本相当于一个线性函数,也就是多层神经网络变化之后基本相当于在做线性变换,就变成一个接近线性变化的值
dropout 正则化
dropout正则化,也就是丢弃法正则化,也成为随机失活正则化。
对每个点进行抛硬币,50%的概率丢弃该点,得到一个丢弃一部分的神经网络,这个方法虽然听上去不可靠,但是实际表现却不错
随机失活正则化的实现方法:
假设有一个L=3的神经网络,先设置一个保留率keep-prob,随机产生一个3*n的矩阵,与keep-prob比较之后产生d3,让原本的w乘以这个d3,再除以一个keep-prob以消除引入随机失活的影响(因为你引入随机失活,相当于对某层的a乘以一个keep-prob,那么我要结果一样,就要除以一个keep-prob)
举个例子为什么要除以keep-prob,比如我们现在第三层有50个点,如果keep-prob为0.8的话,那么这层大概平均来说有10个点要失效,$z^{[4]}=w^{[4]}a^{[3]}+b^{[4]}$,那么此时的$a^{[3]}$的期望就变成了原来的80%,为了使得$z^{[4]}$的期望不变,我们就需要将$a^{[3]}$除以一个keep-prob来确保$z^{[4]}$期望不变。

随机失活正则化的理解
直观解释:因为你不知道哪一个神经元可能被丢弃,所以你不能过分依赖某个神经元,因此权重就不得不分散
在真正使用的时候,如果你担心某层容易过拟合,那么就把这一层的留存率设置的低一些;如果确认不会过拟合,那就把留存率设置接近1,比如在输入层这里留存率就应该是1
其它正则化方法
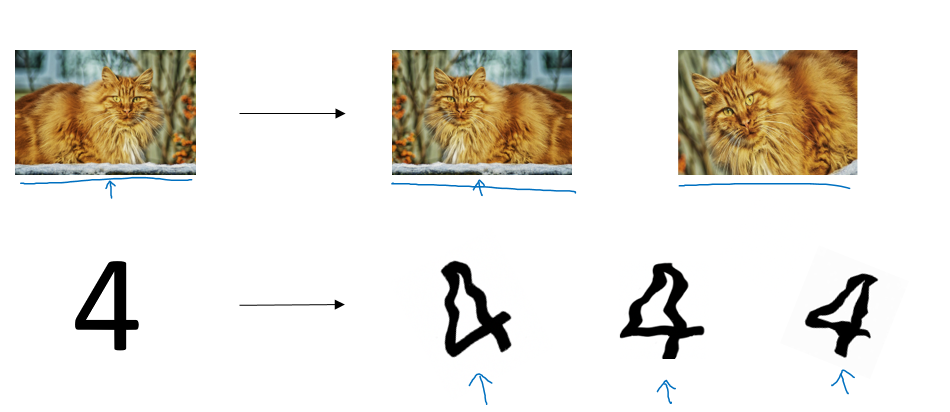
在图片处理的时候,如果你没有更多的数据,比如处理猫之类的:你可以将图片进行水平翻转,或者放大旋转之类的,处理数字的时候:可以扭曲加旋转
另一种方法叫做早终止方法(early stopping)
画出训练集的代价函数和开发集的代价函数,选择两者都还比较小的值
归一化(normalization)
归一化可以加速训练过程
归一化的过程:减去均值($x-\mu$),将方差归一化$(x-\mu)/\sigma$
归一化过程中一定要注意,对训练集和测试集都需要归一化
梯度消失和梯度爆炸
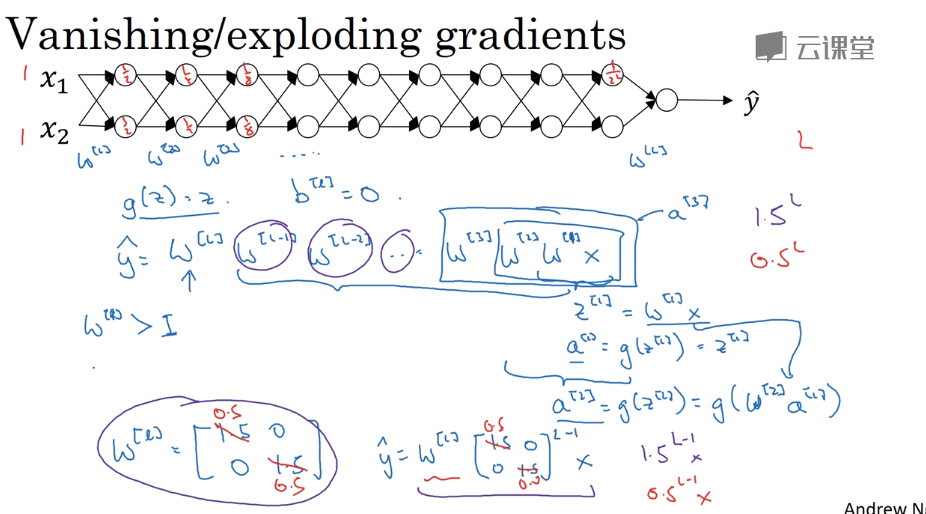
由于:
$$a^{[l]}=\sigma(w^{[l]}a^{[l-1]}+b^{[l]}) \tag{1}$$
$$a^{[l-1]}=\sigma(w^{[l-1]}a^{[l-2]}+b^{[l-1]}) \tag{2}$$
$$a^{[l-2]}=\sigma(w^{[l-2]}a^{[l-3]}+b^{[l-2]}) \tag{3}$$
求导可得
$dz^{[l]}=da^{[l]} * {g^{[l]}}’(z^{[l]}) \tag{4}$
$dw^{[l]}=dz^{[l]}*a^{[l-1]}\tag{5} $
$db^{[l]}=dz^{[l]}\tag{6}$
接着求前一层:
由上面公式(1)可以得到:
$da^{[l-1]}=dz^{[l]}*w^{[l]}\tag{7}$
由公式(2)得到:
$dz^{[l-1]}=da^{[l-1]} * {g^{[l-1]}}’(z^{[l-1]}) \tag{8}$
$dw^{[l-1]}=dz^{[l-1]}*a^{[l-2]} \tag{9}$
结合(7),(8),(9)得到:
$dw^{[l-1]}=dz^{[l]}w^{[l]} {g^{[l-1]}}’(z^{[l-1]}) \tag{10}$
继续对(3)进行求导:
$dz^{[l-2]}=da^{[l-2]} * {g^{[l-2]}}’(z^{[l-2]}) \tag{11}$
$dw^{[l-2]}=dz^{[l-2]}*a^{[l-3]} \tag{12}$
由公式(2)得到:
$da^{[l-2]}=dz^{[l-1]}*w^{[l-1]}\tag{13}$
结合(11),(12),(13)得到:
$dw^{[l-2]}=dz^{[l-1]}w^{[l-1]}{g^{[l-2]}}’(z^{[l-2]})*a^{[l-3]}$
再结合(4),(7),(8)可得
$dw^{[l-2]}=da^{[l]}w^{[l]}w^{[l-1]}{g^{[l]}}’(z^{[l]}){g^{[l-1]}}’(z^{[l-1]}) *{g^{[l-2]}}’(z^{[l-2]})*a^{[l-3]}$
比如你的激活函数是g(z)=z,损失函数是交叉熵函数,$da=a-y$然后$dw^{[1]}=w^{[l]}\times w^{[l-1]}\times…\times w^{[2]}\times w^{[1]}\times X$,只要所有w都是对角矩阵,他的某一项大于1,则出现梯度爆炸,求出的梯度非常大,或者是梯度消失,求出的梯度基本为0
权重初始化和深度网络
特殊地初始化可以部分解决梯度爆炸和梯度消失的问题
在使用Relu激活函数的时候:
$W^{[L]}=np.random.randn(shape) * np.sqrt(1/n)$
梯度检验
根据导数的定义,对代价函数进行求导:
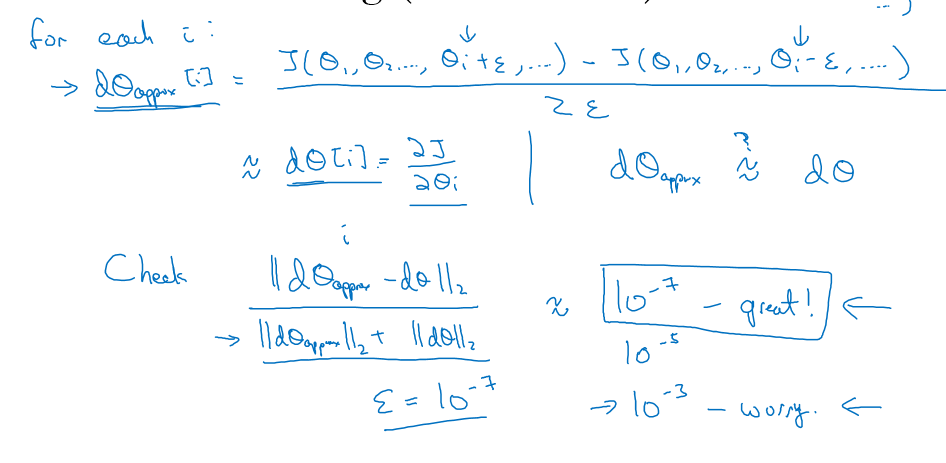
检查:两个导数之间的欧式距离/两个导数的2范数之和,如果基本等于$\epsilon$的话,那就说明正确了,如果大于$\epsilon$很多的话,就说明错了
梯度下降的实现
- 只在调试的时候用提督检验,在训练的时候不要用
- 如果算法梯度检验失败,检查每一个dw,db来找到程序的bug
- 记得正则化
- 在没有dropout的时候先进行梯度检验,发现算法没有问题再使用dropout
- 随机初始化可以先运行一下梯度检验
合适的初始化方法
He初始化方法(He et al., 2015),在激活函数是Relu的时候非常有效,具体做法是$W^{[l]}=\rm{np.random.randn}(layer_dimension[l],layer_dimension[l-1])*\rm{np.sqrt}(2./layer_dimension[l-1])$
第二周
优化算法
向量化可以高效计算m个example,但是当example非常多的时候,计算起来也是非常的慢的,比如你现在有500w个example,拿计算起来就是非常慢的
为了加快计算的速度,提出了mini-batch gradient descent,也就是批量梯度下降,将数据分成一个个的小batch,然后进行前向传播,反向传播,参数更新等步骤,这样计算速度会快上很多
比如现在有500w条数据,将每1000条数据凑成一个batch,用{}来表示第多少个batch,现在分成了$X^1$到$X^5000$共5000个batch,每个batch的维度是$(n_x,1000)$
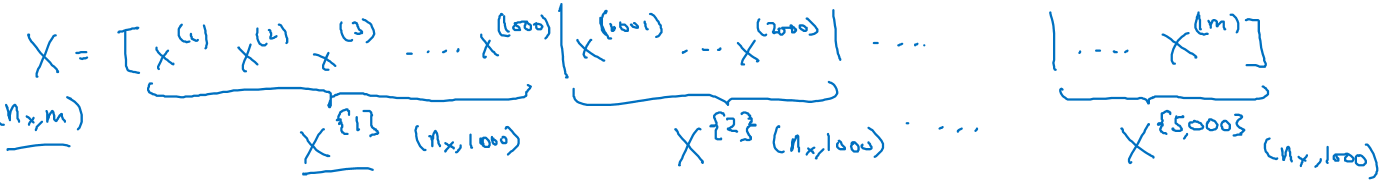
Y以同样的方法被分成5000份,每个$Y^$的维度是(1,1000)
到目前为止,我们一共用过三种括号,分别是小括号,中括号,和大括号
- 小括号:$x^{(i)}$,表示第i个训练实例
- 中括号:$Z^{[L]}$表示第L层
- 大括号:$X^$,$Y^$表示第t个batch
分成batch之后的步骤和之前的神经网络的构建步骤一样,只是多了一重循环batch的for

理解mini-batch梯度下降
批量梯度下降的损失函数往往一直下降,但是mini-batch梯度下降存在噪声,但是整体趋势是下降的
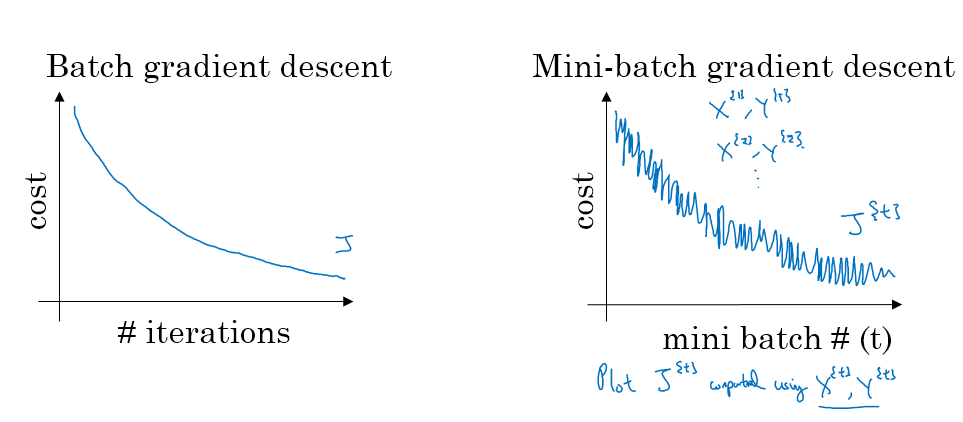
两种极端情况:
- 如果mini-batch的size=m,那么这就是梯度下降,梯度下降的好处是每一步迭代都是往最优值的方向去靠近,但是数据量很大的时候,批量梯度下降就会非常的慢,这种情况又被称为批梯度下降
- 如果mini-batch的size=1,那么这种情况就是每次输入一个example,这样每次迭代的方向可能是乱的,最终的结果可能在最优值附近徘徊,这种情况又被称为随机梯度下降
- 只有mini-batch值合适的时候,才能既用到向量化的加速运算,又能得到一个最优值
一般认为:
在m<=2000时,认为数据量足够下,可以使用批量梯度下降
在m>2000时,通常使用的mini-batch的size为64, 128, 256, 512,用2的倍数是因为内存读取的方式是通过2的倍数来读取的,这样能够加快运算
指数加权平均
如图,是一大堆温度数据,我们为了对温度数据做个平均,用v0=0,$v_1=0.9v_0+0.1\theta_1$,一直到$v_t=0.9v_{t-1}+0.1\theta_t$进行指数加权平均
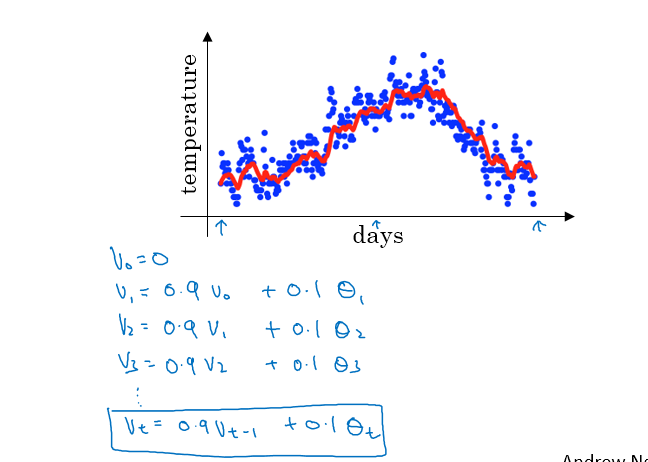
这种指数加权平均的效果的$v_{t}$就大致等同于对$\frac{1}{1-\beta}$天的数据进行平均,其中$\beta$是$v_t=\beta v_{t-1}+(1-\beta)\theta_t$这个公式中的系数
比如,当$\beta=0.9$时,这就相当于对前10天的数据进行平均;当的$\beta=0.98$时,这就相当于对前50天的数据进行平均;当的$\beta=0.5$时,这就相当于对前2天的数据进行平均
更大的$\beta$意味着更平滑的曲线,但是对数据的延迟性也更大
指数加权平均的理解
通用的迭代公式:$v_t=\beta v_{t-1}+(1-\beta)\theta_t $
我们来举个例子,假如$\beta=0.9$
那么
$v_{100}=0.9 v_{99}+0.1\theta_{100}$
$v_{99}=0.9 v_{98}+0.1\theta_{99}$
$v_{98}=0.9 v_{97}+0.1\theta_{98}$
将$v_{100}=0.9 v_{99}+0.1\theta_{100}$展开可以得到
$v_{100}=0.9 v_{99}+0.1\theta_{100}=0.1\theta_{100}+0.9(0.1\theta_{99}+0.9 v_{98})=0.1\theta_{100}+0.9*0.1\theta_{99}+0.9^2(0.9 v_{97}+0.1\theta_{98})…$
这个过程与我们平时的平均数有类似的地方,因为我们平时求解的平均数是在每个$\theta$前面的系数相等,都是1/n,在指数加权平均的时候,将靠的近的系数放大,靠的远的系数变小,以指数形式衰减
这样下去,要使得v的加和的那一项足够小, 也就是$0.1*0.9^{t}$足够小的情况下,$0.9^{10}=1/e$,就认为是10天的平均
指数加权平均的好处:
我们可以看到指数加权平均的求解过程实际上是一个递推的过程,那么这样就会有一个非常大的好处,每当我要求从0到某一时刻(n)的平均值的时候,我并不需要像普通求解平均值的作为,保留所有的时刻值,类和然后除以n。
而是只需要保留0-(n-1)时刻的平均值和n时刻的温度值即可。也就是每次只需要保留常数值,然后进行运算即可,这对于深度学习中的海量数据来说,是一个很好的减少内存和空间的做法。
偏差修正
因为$v_0=0$,而$v_1=0.98v_0+0.02\theta_1$,因为$v_0=0$,所以$v_1=0.02\theta_1$;$v_2=0.98v_1+0.02\theta_2$,$v_2=0.0196\theta_1+0.02\theta_2$
由于上面两个等式展现的原因,这些v的值在初始阶段都很小,为了使这些初始阶段的值可以作为平均,我们用$v_t=\frac{v_t}{1-\beta^t}$来进行偏差修正,如下图

动量(Momentum)梯度下降
动量梯度下降比普通的梯度下降更快,其主要思想是:计算梯度的指数加权平均,使用这个梯度来更新权重
实现的方式如下,$\beta$参数最常用的值就是0.9:
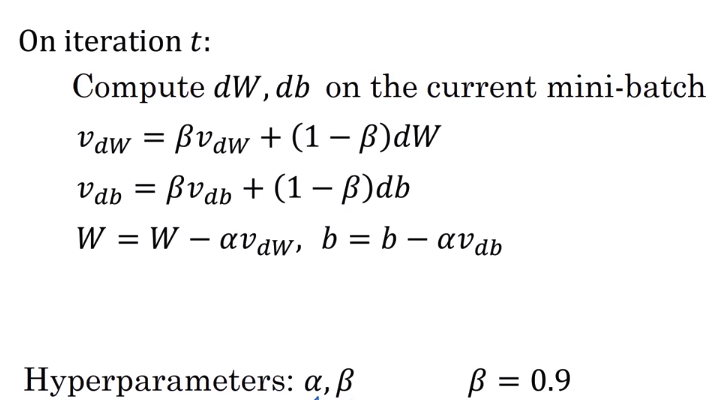
进行动量梯度下降之后,纵轴上的偏差被减小了,得到如下图红线的效果

RMSprop(Root Mean Square prop)算法
实现的方法和momentum类似,但是公式变成了
$S_{dw}=\beta_2S_{dw}+(1-\beta_2)dw^{2}$
$S_{db}=\beta_2S_{db}+(1-\beta_2)db^{2}$
而迭代公式变成了
$w:=w-\alpha\frac{dw}{\sqrt{S_{dw}}+\epsilon}$
$b:=b-\alpha\frac{dw}{\sqrt{S_{db}}+\epsilon}$
加一个$\epsilon$是为了不出现除以0的情况
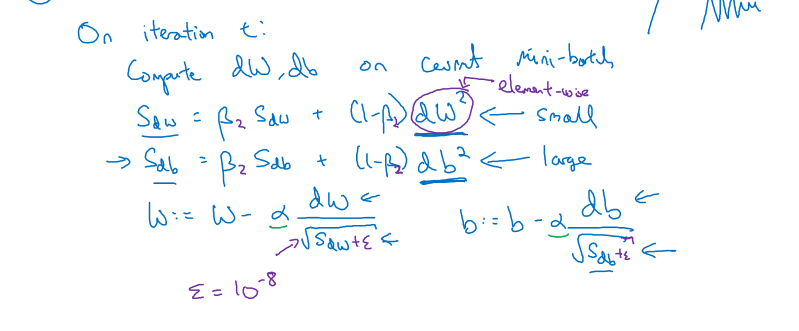
Adam(Adaptive moment estimation) 优化算法
Adam(Adaptive moment estimation)的意思是:适应性矩优化,这里的矩指的是一阶矩,二阶矩那个矩。
Adam就是将momentum和RMSprop结合起来
实现方法如下图,注意这里的参数都需要修正偏差:

里面的超参,一般来说momentum的超参$\beta_1=0.9$,RMSprop的超参$\beta_2=0.999$,$\epsilon=10^{-8}$,学习率$\alpha$ 是需要去调整的参数,Adam的公式如下,将w换成b则得到b的更新公式
$$
\begin{cases}
v_{dW^{[l]}} = \beta_1 v_{dW^{[l]}} + (1 - \beta_1) \frac{\partial \mathcal{J} }{ \partial W^{[l]} } \
v^{corrected}{dW^{[l]}} = \frac{v{dW^{[l]}}}{1 - (\beta_1)^t} \
s_{dW^{[l]}} = \beta_2 s_{dW^{[l]}} + (1 - \beta_2) (\frac{\partial \mathcal{J} }{\partial W^{[l]} })^2 \
s^{corrected}{dW^{[l]}} = \frac{s{dW^{[l]}}}{1 - (\beta_2)^t} \
W^{[l]} = W^{[l]} - \alpha \frac{v^{corrected}{dW^{[l]}}}{\sqrt{s^{corrected}{dW^{[l]}}} + \varepsilon}
\end{cases}
$$
学习率衰减
我们用下面的公式来衰减学习率$\alpha$:
$\alpha=\frac{1}{1+decay_rate\times epoch_num}\alpha_0$
decay_rate是这里的下降率,epoch_num是迭代的次数
局部最优解
在二维图像中,很容易产生局部最优解,但是在高维的时候,你要找到一个这个点在所有维度上梯度都为0,这是非常困难的,我们称这种有部分维度梯度为0的点为鞍点,因为图形的形状就好像马鞍一样
Week 3
Batch Normalization
调参过程
神经网络有很多的超参,调整超参有利于改进神经网络的性能
参数有很多,包括:学习率$\alpha$,momentum当中的$\beta$,Adam优化中的$\beta_1,\beta_2,\epsilon$,网络层数,隐藏单元,学习率衰减方式,mini-batch的size
一般来说需要调整的重要程度排序为:
$\alpha>\rm{momentum当中的}\beta=mini-batch\ size=隐藏单元数量>网络层数>学习率衰减参数>>Adam(Adam一般不调参,用默认参数\beta_1=0.9,\beta_2=0.999,\epsilon=10^{-8})$
但这并不是一个死板的规定,可能有其他的规则
早期调参的时候,通常是启发式搜索,然后给定最优的参数;参数很多的时候,建议随机选择点,进行尝试,如下图右边
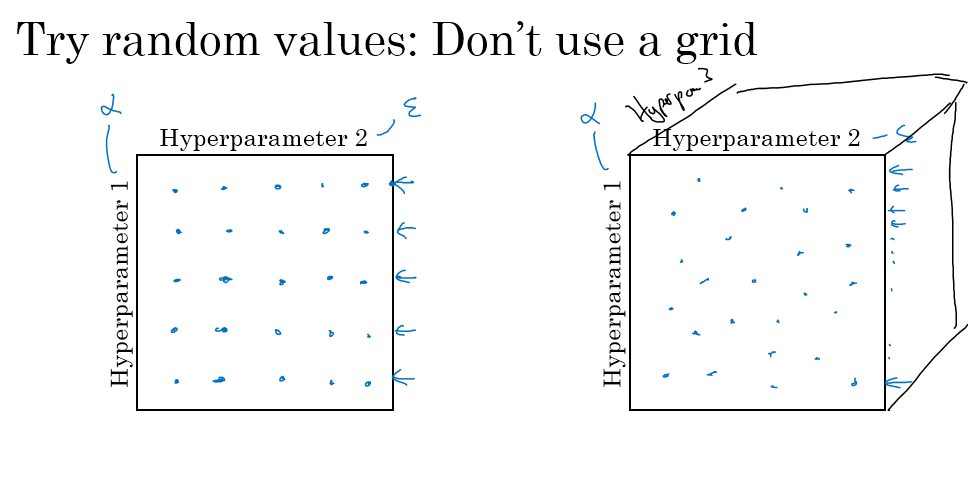
当你能确定更小的范围的时候,就可以在这个范围内进行更加密集的搜索,直到找到你能接受的最优参数
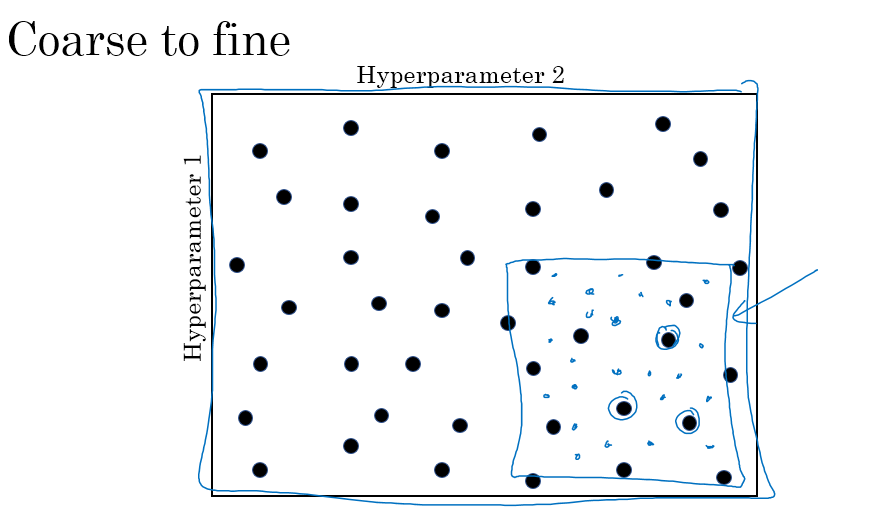
选择合适尺度去选取超参数
很多超参数是不能在某个范围内均匀取样的,比如考虑学习率$\alpha$,让$\alpha$从0.0001到1取值,肯定要求在0.0001到0.001之前取多点,而0.1-1之间要比较少,所以我们此时用到对数的取法,也就是从10e-4取到10e0,那我们就只需要去一个-4到0的随机数,用a = -4 * np.random.randn(), alpha=10**a
还有比如momentum当中的$\beta$参数,如果让$\beta$从0.9取到0.999,在靠近0.999的时候,稍微改变一点点都会让平均值的范围变化很大,因此在后面我们要取的密集一些,我们考虑$1-\beta$,$\beta$从0.9到0.999,那么$1-\beta$就从0.1到0.001,取一个从-3到-1的随机数,再用10的指数来代替$1-\beta$,那么$\beta=1-10^t$
熊猫模型和鱼子酱模型
熊猫模型:关注你的模型,就如同熊猫产子一般,一次调整一点
鱼子酱模型:一次同时开始多个模型的训练,如同鱼类产子一般
计算资源足够的时候,就用鱼子酱模型,否则用熊猫模型
这两个名称只是为了好记忆,并没有特别的意思
批量归一化
在之前的归一化当中,我们只是对第一步的输入进行了归一化,但是其实每一层神经网络的输入应该都有归一化,在归一化z和a这两种选择中,业界都默认归一化z
对z的归一化过程如下:

红框部分就是归一化的过程,对于每一个z(i),计算均值$\mu$,方差$\sigma^2$,然后用$z^{(i)}{norm}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\epsilon}}$,这里加一个$\epsilon$的原因是为了避免除以0的情况发生,然后用$\tilde{z}^{(i)}=\gamma z^{(i)}{norm}+\beta$,这个$\gamma$和$\beta$是可以从模型当中学习出来的参数。
为什么要用$\gamma$和$\beta$这两个参数呢,是因为比如你中间某一层的激活函数是sigmoid函数,如果你让你的z均值为0,方差为1,那么z的变化范围就很靠近0,这是sigmoid函数基本就成了线性函数,为了利用好sigmoid的非线性,所以对中间的z的归一化稍有不同
将batch-norm运用到神经网络中
假设我们有一个如下图所示的三层神经网络,那么我们将x输入,通过w[1]和b[1],得到z[1],对z1进行batch-norm,通过$\gamma^{[1]}$和$\beta^{[1]}$得到$\tilde{z}^{[1]}$,然后将$\tilde{z}^{[1]}$通过g[1]得到a[1],同理得到z[2],$\tilde{z}^{[2]}$,a[2]
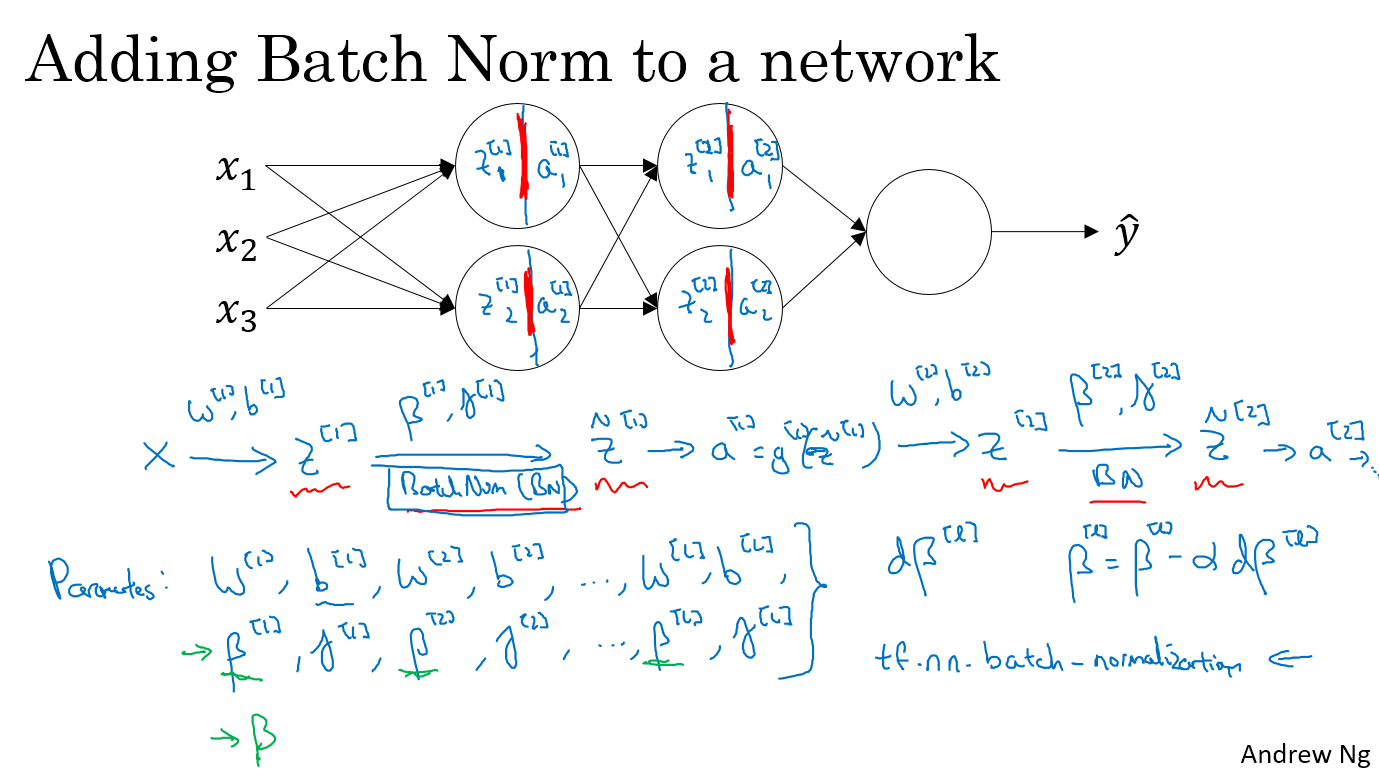
此时的参数就有了w[1],b[1],w[2],b[2],$\gamma^{[1]}$,$\beta^{[1]}$,$\gamma^{[2]}$,$\beta^{[2]}$,在TensorFlow中我们可以直接一行语句实现batch-normalization,tf.nn.batch-normalization
那如何将batch-normalization用到mini-batch-normalization中呢
如下图,每次用一个mini-batch,对其进行batch-normalization。
值得注意的是,因为$z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$,而$z_{norm}=\frac{z-\mu}{\sqrt{\sigma^2+\epsilon}}$,每次归一化的时候减去了均值,所以加的$b^{[l]}$会被减掉,因此b这个参数在mini-batch-normalization时可以忽略

实现的具体方法,对于每一次mini-batch t,计算对于$X^{[t]}$的前向传播,对每个隐藏层使用BN(batch-normalization)方法,然后反向传播去更新W,$\beta$,$\gamma$三个参数(b被减掉因此忽略),当然这里更新的方式可以是momentum,RMSprop或者Adam

为什么batch-normalization会有效
首先,normalization会使得所有的x的值在同一个量级上面,这样能够加速迭代
协变量转换(covariate shift)是指在数据x变化之后,原来的网络不适用于分类新的数据的情况,如果我们使用了batch-normalization方法,前面层的变化对后面层的影响就降低了,因为被平均了,所以BN会使得系统优化的结果更好
同时,这还起到了一点点正则化的作用,因为每个mini-batch在计算的时候都被平均了,所以整个网络对于数据的适应性就没有那么强了
对测试数据的batch norm
在训练阶段,我们每次可以用一次批量的值计算均值和方差,但是在测试阶段,我们每次输入的只有一个值,这时候我们进行batch norm的均值和方差从哪里来呢?
解决办法就是,记录下训练数据的均值和方差,然后对各个mini-batch norm的均值和方差做指数权重平均,在测试阶段使用
多分类
softmax Regression
我们之前接触的问题都是二分类,当我们要进行多分类的时候,就要用到一个特殊的激活函数,叫做softmax
假设我们要分类的类别数C=4,标签为0,1,2,3,那么在最后一层,我们要输出一个4*1的输出层,每一个输出点代表分到该类的概率
举个例子,我们得到了最后一层的输入为z[L] = [5,2,-1,3],我们用指数函数对其变换,$t = [e^5,e^2,e^{-1},e^3]$,计算比例得到$a^{[L]}$,如下图所示
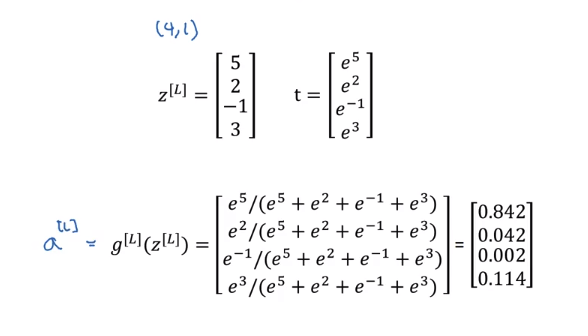
对softmax的理解
softmax是一个$\frac{e^{z_j}}{\sum_ke^{z_k}}$形式的激活函数,当分类的类别C=2的时候,softmax就是logistics函数
softmax的loss一般取为:$L(\hat{y},y)=-\sum_{j=1}^Cy_j\log \hat{y}_j$
真实的y和$\hat y$的形式如下:
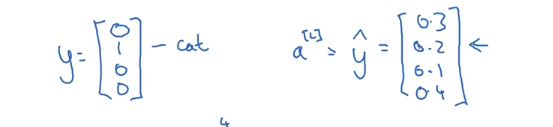
真实值只有真的那个地方为1,别的地方为0,$\hat y$是C个概率,代表分到每一类的概率
因为y一般有很多个需要分类的样本,所以真实的y和$\hat y$如下,其中的4是此时分为4类
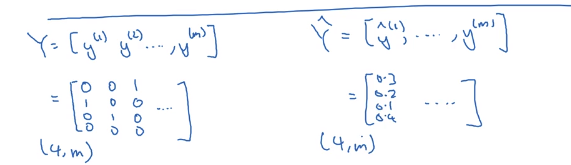
反向传播中,softmax的导数的求法稍微复杂一点,过程如下:
首先求$\partial J/\partial a$,虽然这里有个累加,但是其实只有真实的那类$y_j=1$,别的都是0,所以求和号可以去掉,变成$J=y_j\log \hat{y}_j$,对$\hat y$求偏导可以得到,$\partial J/\partial a=-1/\hat{y}_j$
接下来求softmax的导数,也就是$\hat{y}_j$对所有的$z_i$求导数,分为i=j和i!=j的情况来求
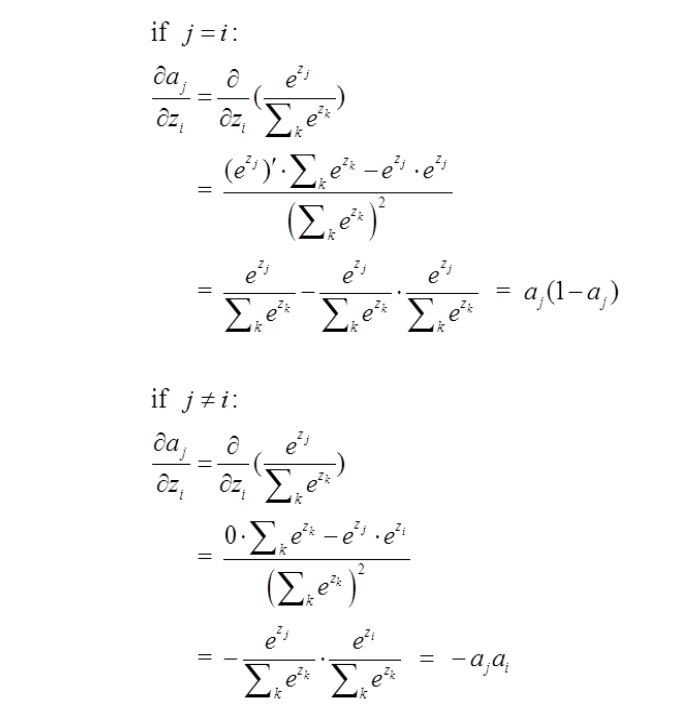
这样,$\partial J/\partial z$的值就可以通过链式法则得到
当i=j时,$\partial J/\partial z=a_j-1$
当i!=j时,$\partial J/\partial z=-a_i$
在使用深度学习框架的时候,比如TensorFlow和caffe,我们只需要规划好前向传播的过程,反向传播的过程框架会自动帮你完成
深度学习框架的介绍
目前主流的深度学习框架和选择标准如下:

TensorFlow简介
引入TensorFlow,通过import tensorflow as tf
w设置为tf当中的变量,用tf.Variable(initial_value=0,dtype=tf.float32)表示
x是输入值,一开始不知道是多少,只表示dtype和shape,用tf.placeholder(dtype=tf.float32,shape=[3,1])表示
表示cost函数,因为tf已经重载了加减乘除的形式,所以可以直接用加减乘除表示,也可以用tf.add之类的表示,矩阵乘法的表示是tf.matmul()
之后表示train的方法和目标:我们这里用梯度下降,最小化costtrain = tf.train.GradientDescentOptimizer(0.01).minimize(cost),如果要用别的优化方法,只需要将GradientDescentOptimizer替换为别的函数就好了,括号里面的参数是learning-rate
然后初始化变量值,init = tf.global_variables_initializer()
定义一个session,用session来run一下init,再run一下w,看看w的值,最后迭代run(train)
也可以用如下形式定义session
1 | with tf.Session() as session: |
placeholder的值可以用feed_dict传入
1 | sess = tf.Session() |
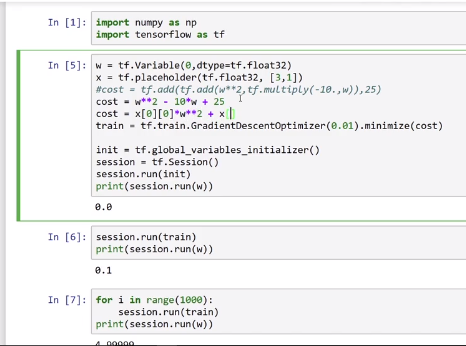
写TensorFlow的代码过程大致如下:
- 建立未执行的tensor变量
- 写tensor之间的运算
- 初始化tensor
- 建立session
- 运行session,将会运行你简历里的运算
所有的运算都要run之后才能执行,如果你直接print运算的话,只会得到一个tensor,也就是计算图
因此,请注意初始化变量,建立session并run operation
损失计算
计算形如:
$$ J = - \frac{1}{m} \sum_{i = 1}^m \large ( \small y^{(i)} \log a^{ [2] (i)} + (1-y^{(i)})\log (1-a^{ [2] (i)} )\large )\small$$
这样的损失的时候,可以使用tf内置的tf.nn.sigmoid_cross_entropy_with_logits函数实现
one_hot encoding
one_hot:只有一个值为1,别的值都为0的vector,用tf.one_hot实现,参数indices表示需要转换的向量, depth表示一共多少个类, on_value=None表示符合类的值为多少, off_value=None表示不符合类的值是多少, axis为0表示每个indices放一行,-1表示每个indices放一列
实现TensorFlow model的步骤
- 建立一个计算图
- run这个计算图
初始化参数的方法
W用Xavier初始化,b用zero初始化
1 | W1 = tf.get_variable("W1", [25,12288], initializer = tf.contrib.layers.xavier_initializer()) |
反向传播的方法
1 | #For instance, for gradient descent the optimizer would be: |