Coursera上面关于deeplearning.ai的课程一共有五门,在申请助学金之后都可以免费参与,这篇博文主要讲的是关于deeplearning.ai的第一门课程的
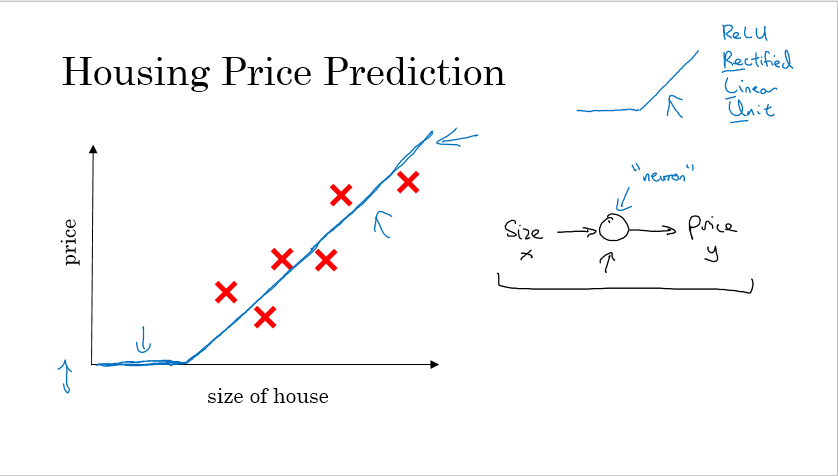
在房价预测中,最普通的如右上角转弯的函数,称之为ReLU(rectified linear unit)函数,给定一个大小,通过一个神经元就可以得到房子的价格,这就是一个神经元。
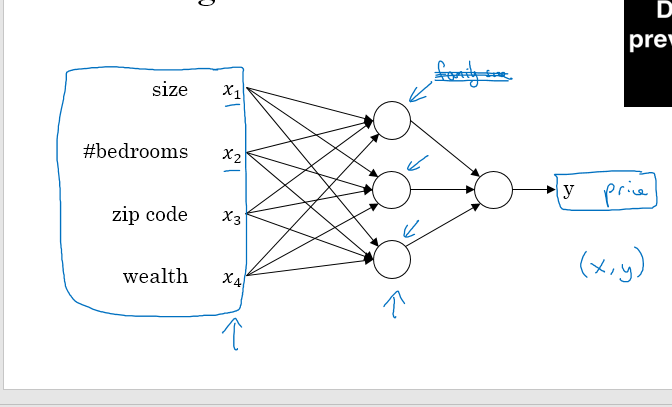
如果你对房价预测还有别的因素,比如卧室的数量,地理位置,学区信息等等来对房价进行预测,你只需要给定大量的x的输入数据,就可以用来预测房价y的值,这样就得到了一个较大的神经元
最左边的一层是输入层,中间一层是隐藏层,最后是输出层
Week 2
首先介绍一下logistics二分类:经典的二分类算法
首先来看看图像分类的问题,输入一张图片,我们标记1作为猫,标记0作为不是猫
图片在电脑中保存为红绿蓝三个色彩强度矩阵,如果是一幅$64\times64$的图片,就有3个$64\times64$的色彩矩阵,为了进行分类,将这些矩阵中的像素值展开为一个向量x作为算法的输入
输入x的定义为:红黄蓝三张矩阵的像素值按顺序放进去,x在$64\times64$的图片的情况下就是,$64\times64\times3=(12288,1)$的矩阵,有m个训练数据,则有m个x向量,m个y
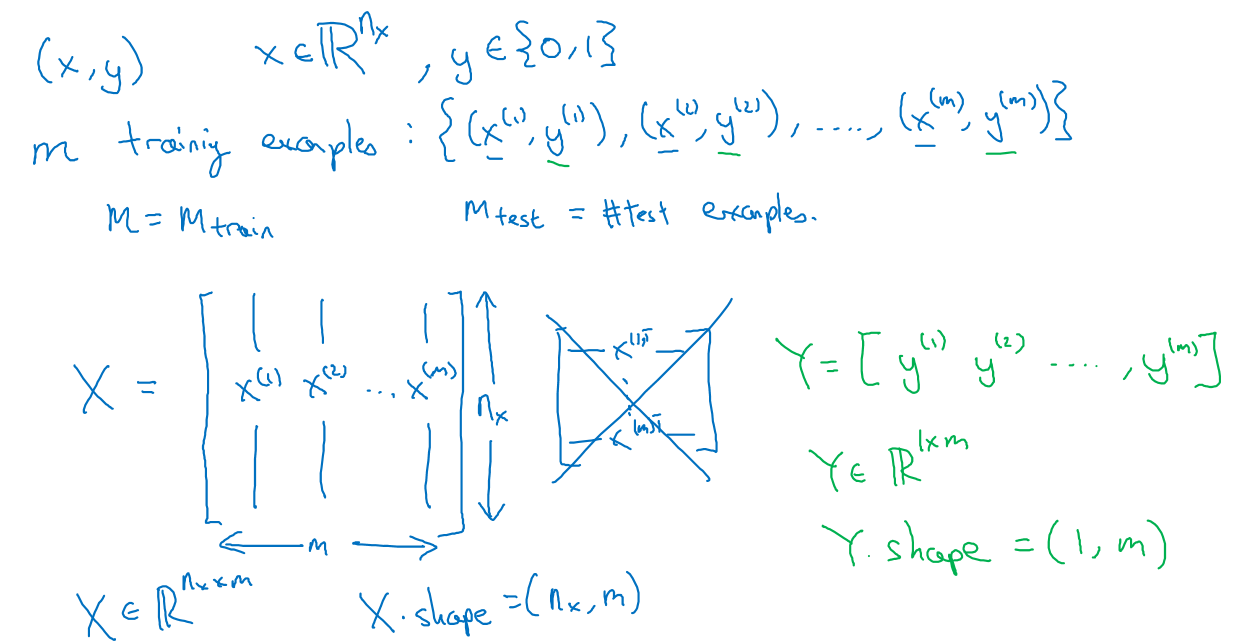
如图,每个训练数据占一列,m个训练数据,一共是$mn$行,Y是标签,m个标签为1m
logistics 回归
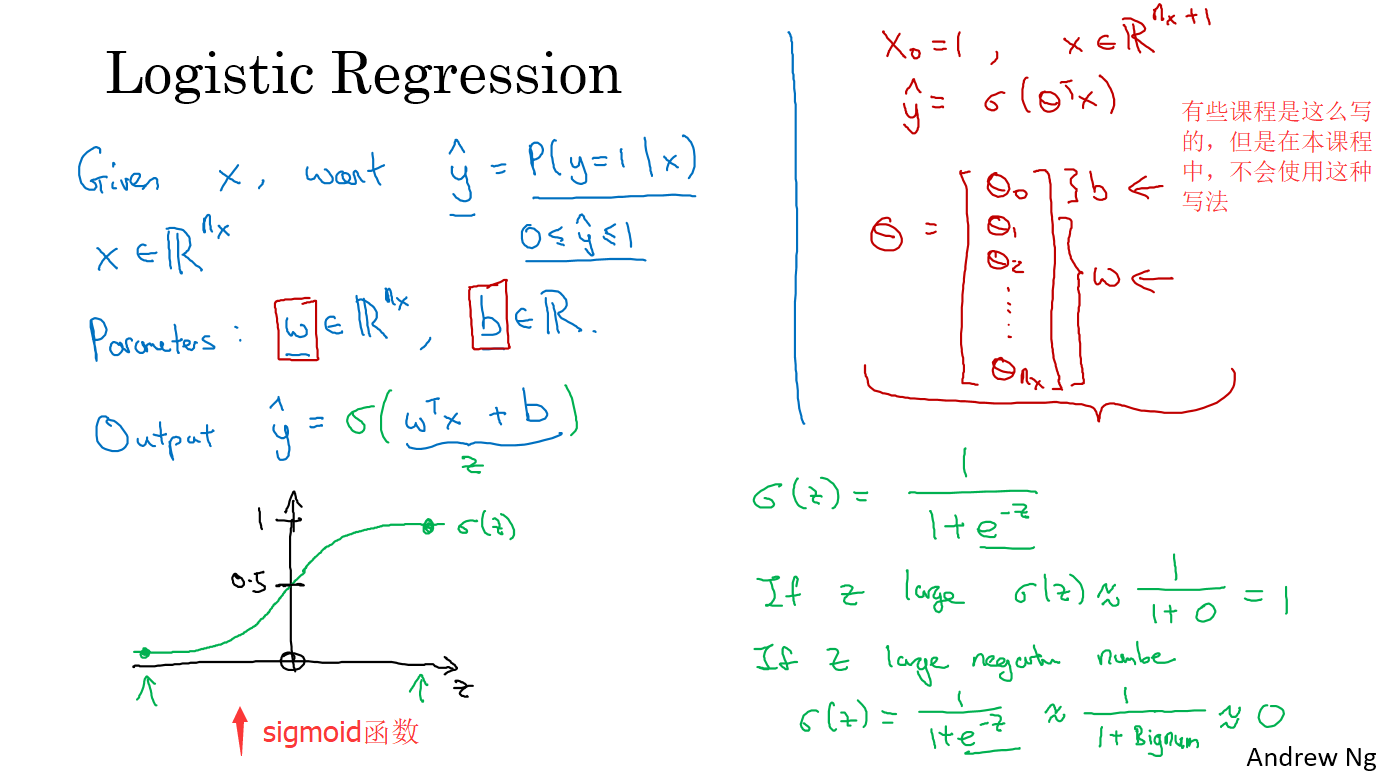
给定x,预测y,y只能是0和1,也就是二分类问题
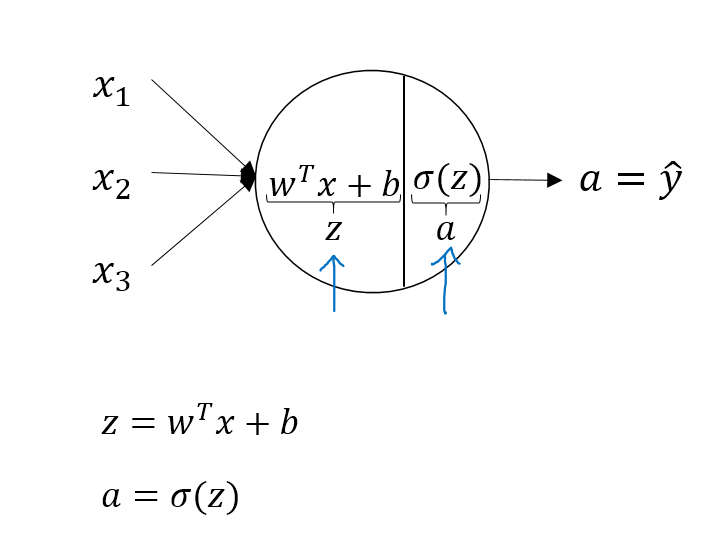
有两个参数,w和b,w也是(n,1)的向量,$\hat{y} = w^Tx+b$,这样的表示并不好,因为y可能是一个小数或者甚至是负数,我们想要结果是0或1,因此我们对结果用sigmoid函数,如下:
$\hat{y} = \sigma(w^Tx+b)$
sigmoid函数的定义为:$f(z)=\frac{1}{1+e^{-z}}$
Logistic Regression Cost Function
为了优化logistic回归的w和b,我们定义一个损失函数,
损失函数(loss function):定义一个估计量$\hat{y}$和一个真实值$y$之间的误差,我们在这里用到的是平方损失函数,$L(\hat{y},y)=\frac{1}{2}(\hat{y}-y)^2$
另一种适用的损失函数定义为:$L(\hat{y},y)=- (y\log\hat{y}+(1-y)\log({1-\hat{y}}))$
- 这个函数在y=1的时候,$L(\hat{y},y)=- \log\hat{y}$,要让损失函数尽可能小,那么$\hat{y}$就要尽可能大(因为前面有负号,log是增函数),由于$\hat{y}$是sigmoid函数,最大为1
- 这个函数在y=0的时候,$L(\hat{y},y)=- \log({1-\hat{y}})$,要让损失函数尽可能小,那么$\hat{y}$就要尽可能小(因为前面有负号,log是增函数),由于$\hat{y}$是sigmoid函数,最小为0
代价函数(cost function):定义整个训练集的平均损失:$J(\hat{y},y)=\frac{1}{m}\sum_{i=1}^{n}L(\hat{y}^{(i)},y^{(i)})$
梯度下降
已经知道了逻辑回归算法的参数w和b,以及代价函数$J(\hat{y},y)$,我们需要一个方法来训练我们的模型,那就是梯度下降。
目标是使代价函数$J(\hat{y},y)$最小,也就是下面这个公式最小:
$J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})=\frac{1}{m}y^{(i)}\log\hat{y}^{(i)}+(1-y^{(i)})\log(1-\hat{y}^{(i)})$
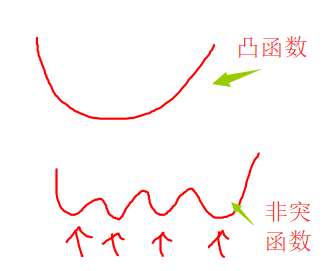
这是一个凸优化问题,有且仅有一个最优值,在初始化w和b的时候,可以令初始w=1,b=0,也可以随机初始化。
每次迭代找到下一个点的方法是通过找到斜率的方向,因为斜率的方向是下降最快的
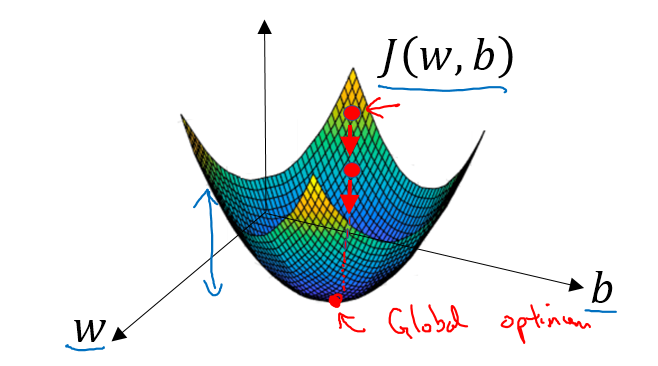
直到找到全局最优值,w和b每次迭代更新的公式如下:
$w:=w-\alpha\frac{\partial{J(w,b)}}{\partial{w}}$
$b:=b-\alpha\frac{\partial{J(w,b)}}{\partial{b}}$
计算图
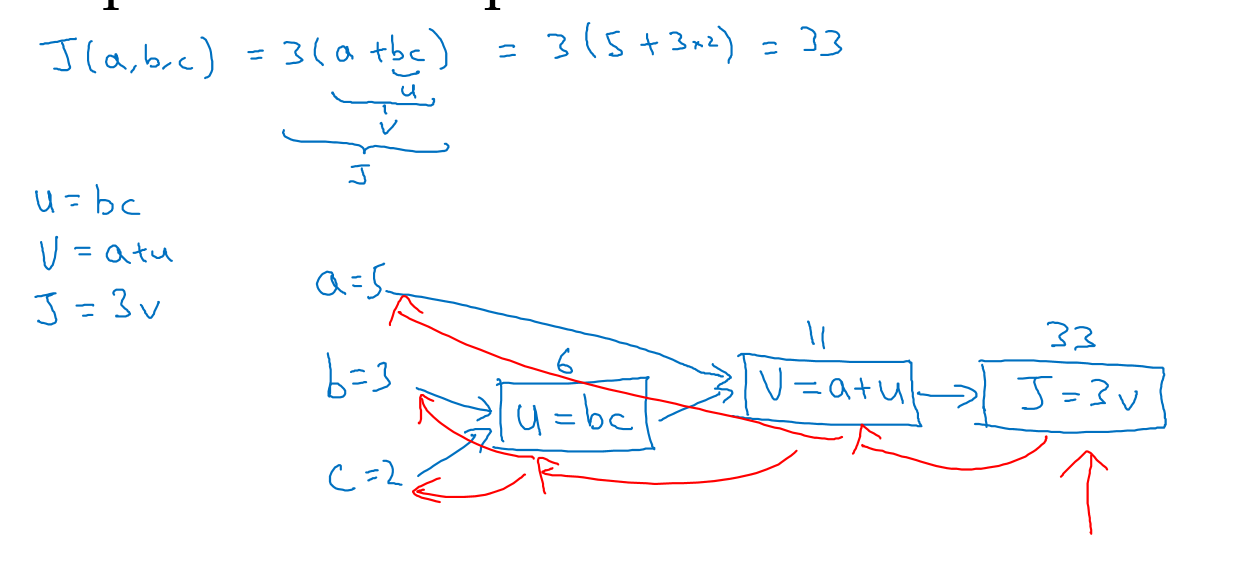
如图是一个计算图,$J(a,b,c)=3(a+bc)$,令bc=u,bc=v,3v=j,这样就是如上图一步一步的计算
在代码中,我们要表示dJ/da的时候,只需要写da就行了
所谓的反向传播,就是通过链式法则求导倒数的过程
logistic回归梯度下降法应用
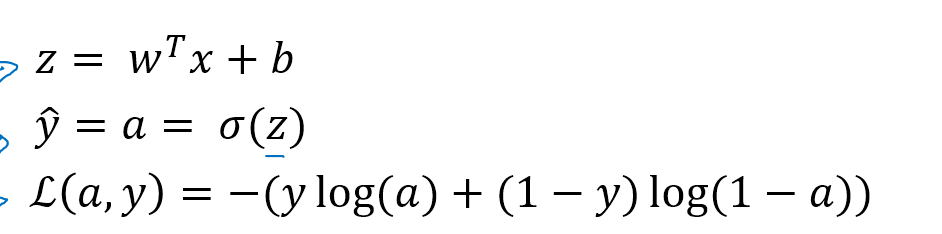
已知z,$\hat{y}$,以及L(a,y)公式如上,要通过调节w和b得到最大或者最小的L,应该用L对w和b求偏导,然后运用
$$w:=w-\alpha dw$$
$$b:=b-\alpha db$$
这两个公式进行迭代,其中dw就是L对w的偏导,db就L对b的偏导
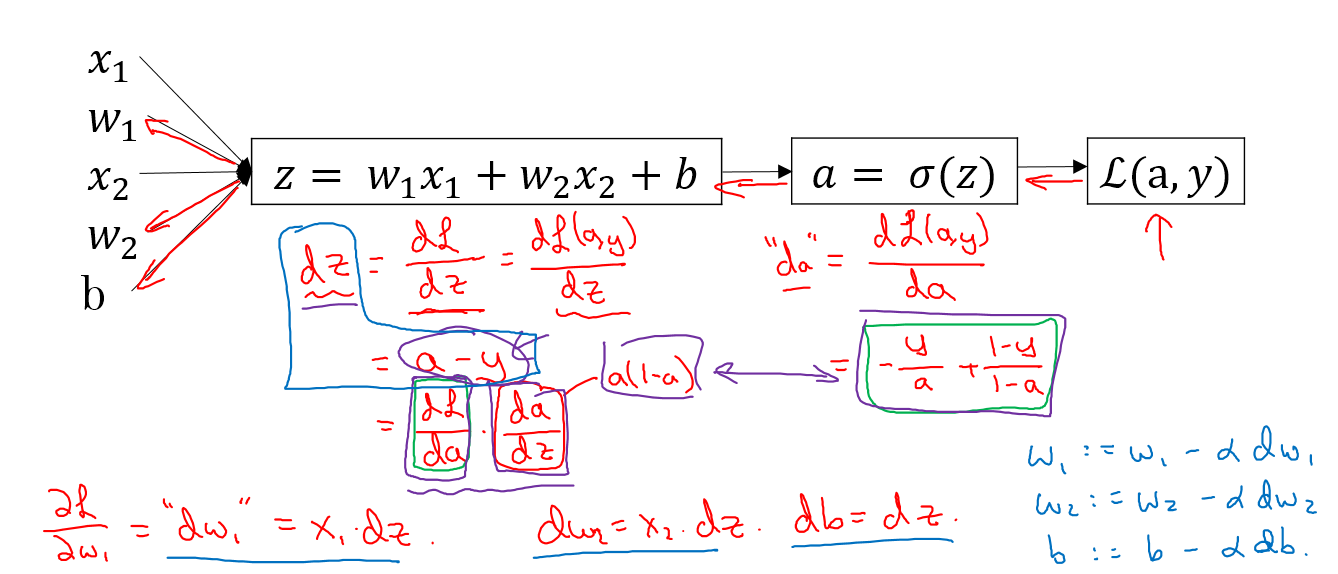
首先L对a求偏导,得到$da=-\frac{y}{a}+\frac{1-y}{1-a}$,接下来a对z求偏导,乘以L对a求偏导,得到$dz=\frac{dL}{dz}=\frac{dL}{da}\frac{da}{dz}$,有
$\frac{da}{dz}=(\frac{1}{1+e^{-z}})’=\frac{e^{-z}}{(1+e^{-z})^2}=\frac{1+e^{-z}-1}{(1+e^{-z})^2}=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=f(z)(1-f(z))=a(1-a)$
因此,$dz=a-y$,$dw_1=x_1dz$,$dw_2=x_2dz$,$db=dz$,再用上图右下角的迭代公式,即可实现梯度下降迭代
m个训练数据的梯度下降
代价函数$J(w,b)=\frac{1}{m}\sum_{i=1}^{n}L(a^{(i)},y^{(i)})$
其中$a^{(i)}=\hat{y}^{(i)}=\sigma(w^Tx^{(i)}+b)$
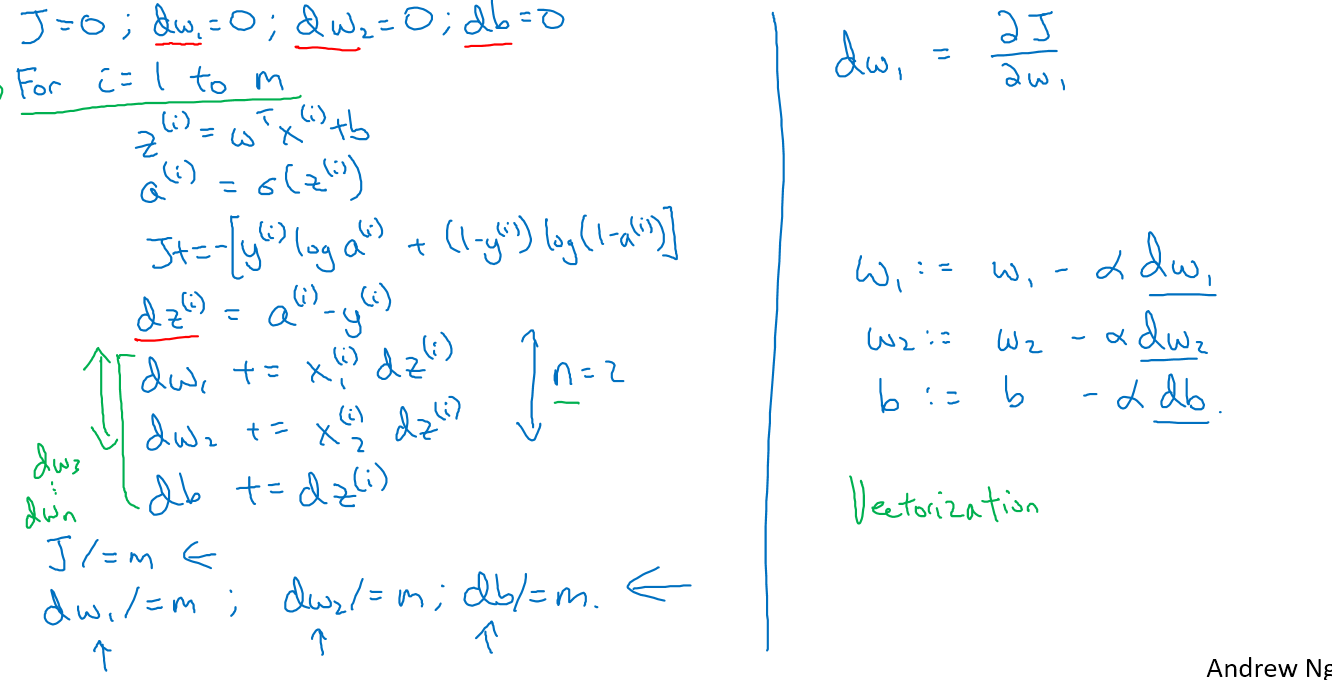
如图,有两层循环,第一层是循环m个训练数据,第二层是循环n个w
通过向量化减少逻辑回归的循环
如下图,我们先减少内层的n个w的循环,通过$dw+=x^{(i)}dz^{(i)}$减少内层循环

我们再来减少外层的循环
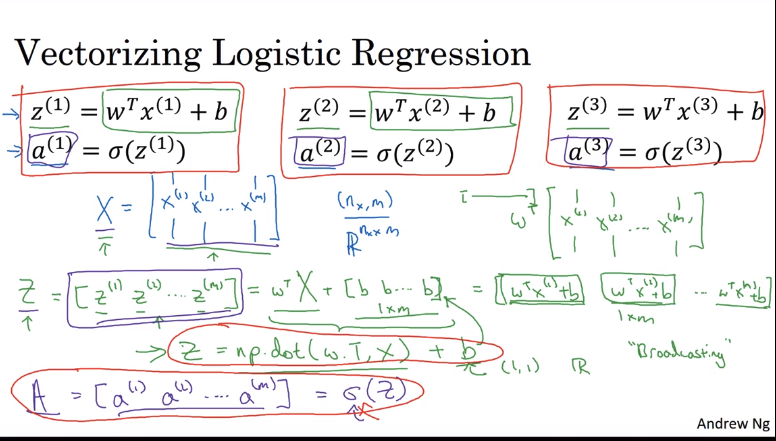
通过图片中Z和A的计算,就可以减少外层的循环


Week 3
神经网络的定义,我们可以从前两周学的逻辑回归来进入,给定x,w,b,可以算出z,由z可以算出a,由a算出损失函数,
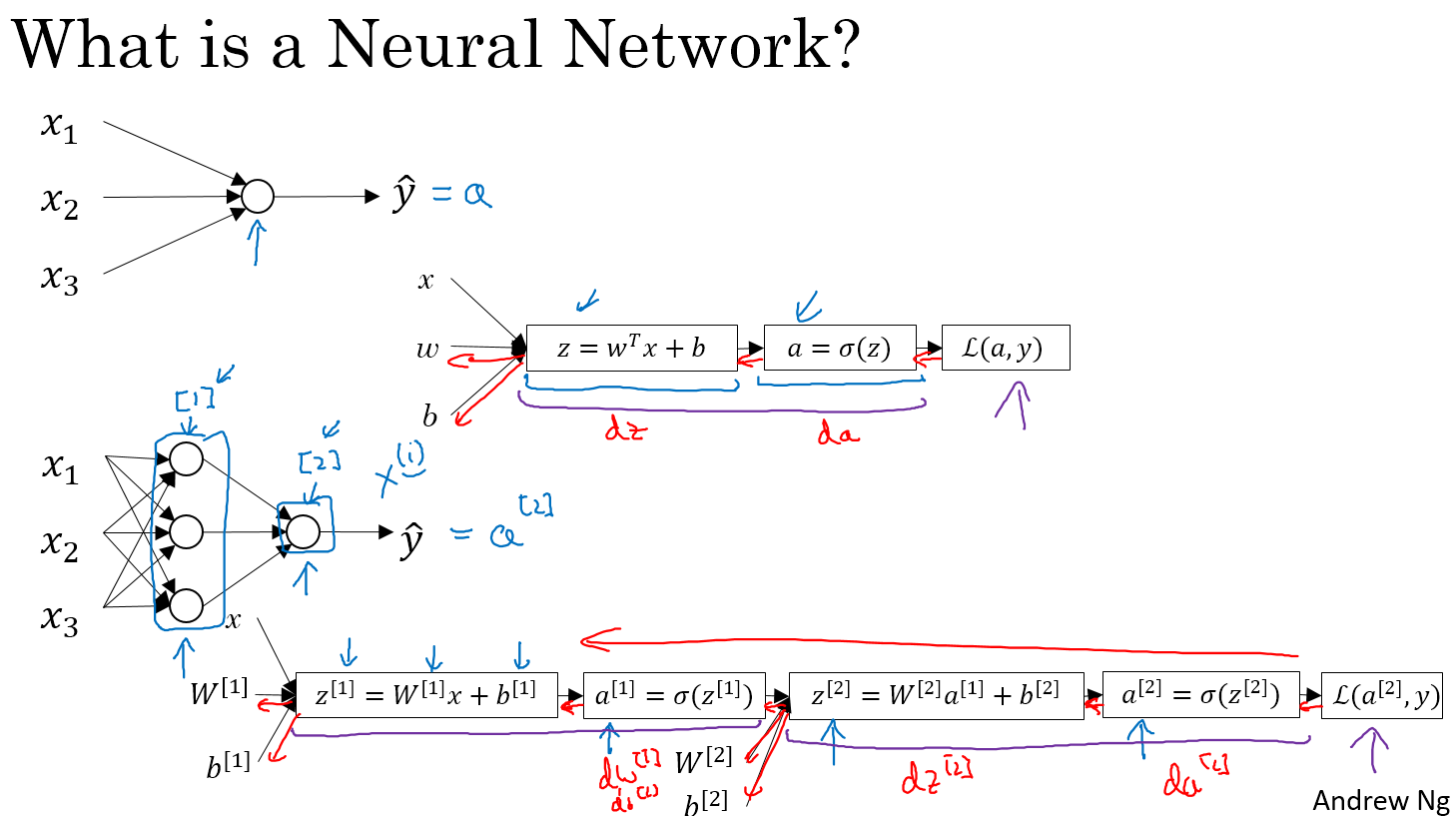
这是一个两层神经网络(包括1个隐藏层和1个输出层,输入层并不算在其中)
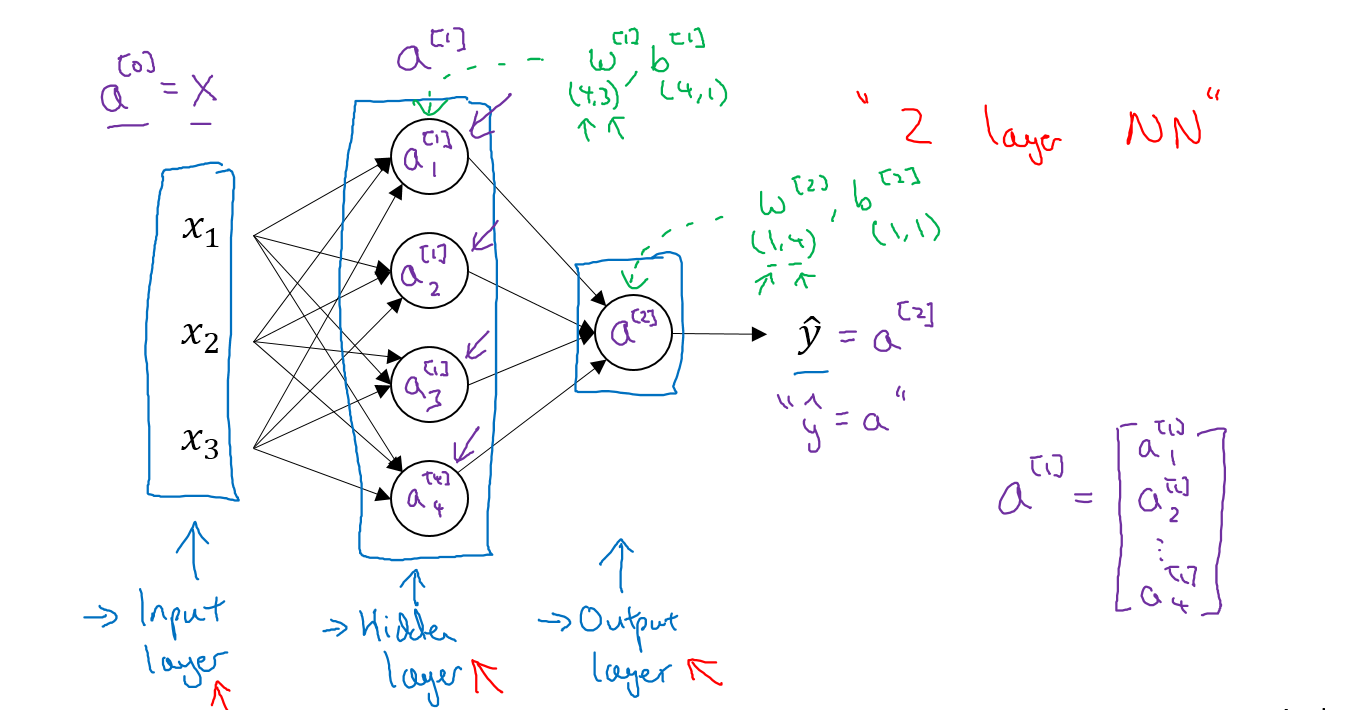
神经网络的计算公式
我们先看看逻辑回归的计算方法:没有隐藏层,直接通过输入就算出最终的输出a
神经网络与之类似,不过多了一层隐藏层,
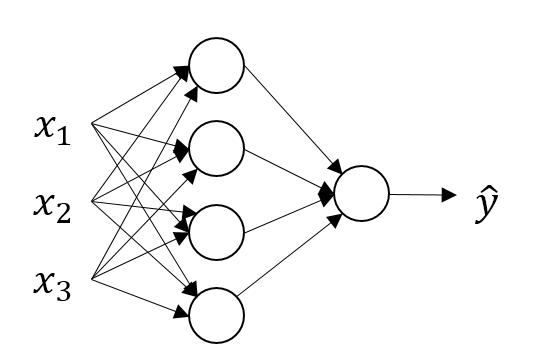
通过如下的公式进行计算隐藏层的每一个点的值
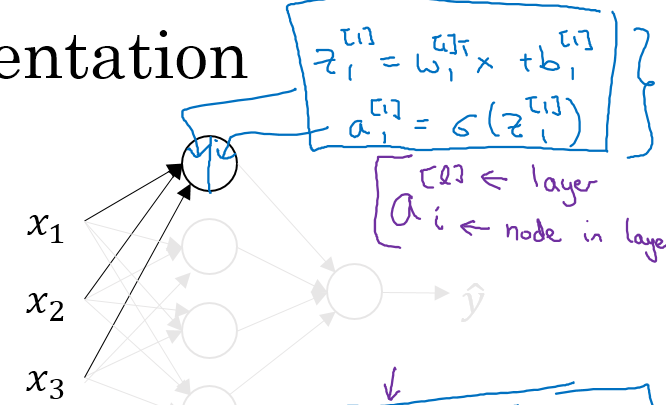
整理一下四个点的计算公式如下:右上角的方括号表示所在层,右下角角标表示第几个点

我们将公式矢量化:
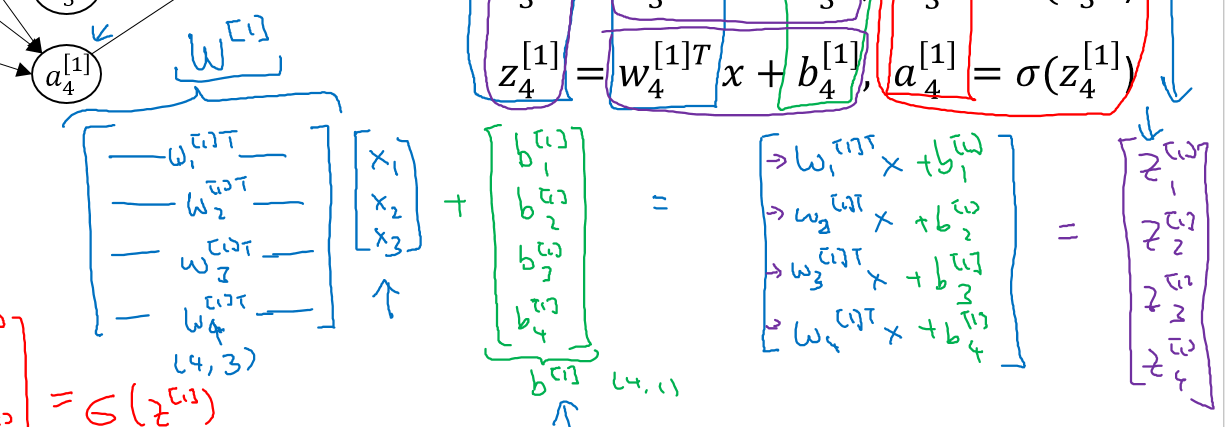
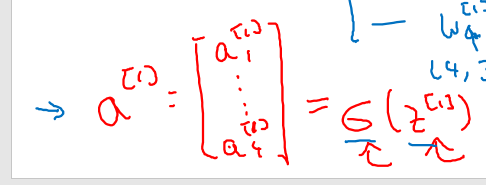
得到最终的计算公式如下:其中a[0]表示输入x
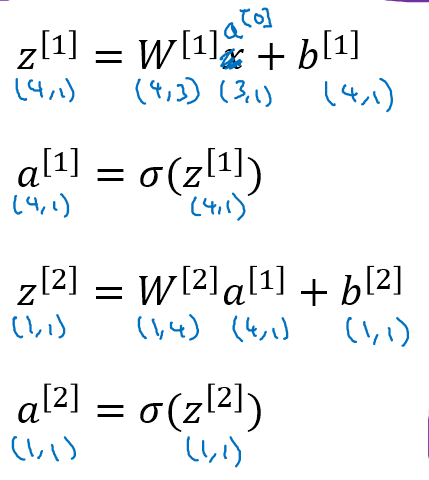
多个训练样本的矢量化
要将如下图所示的循环进行矢量化:其中方括号表示所在层,圆括号表示第几个隐藏单元
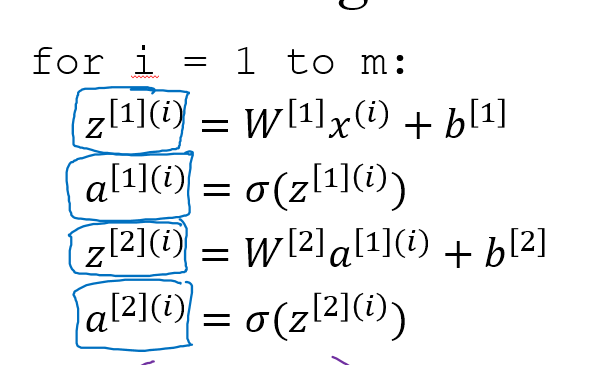
矢量化之后得到如下公式:Z和A的横向表示m个样本
激活函数
我们之前用的激活函数都是simoid函数,tanh函数一般来说比sigmoid函数的效果好
$a = tanh(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}}$
tanh函数可以看做一个sigmoid函数的平移,图形如下:
但是tanh函数和sigmoid函数都有缺陷,那就是在a接近1的时候,斜率非常小,导致迭代速度特别慢,因此给出了RELU函数和leaker relu函数,是Restrict Linear Unit的缩写,一个是取0和z的最大值,一个取0.01z和z的最大值,这样能够保证迭代的速度
为什么需要非线性激活函数
$z^{[1]} = W^{[1]}X+b^{[1]}$
$a^{[1]}=\sigma(z^{[1]})$
$z^{[2]} = W^{[2]}X+b^{[2]}$
$a^{[2]}=\sigma(z^{[2]})$
如果我们不使用非线性激活函数,比如直接让g(z) = z,那么$z^{[2]} = W^{[2]}a^{[1]}+b^{[2]}=W^{[2]}(W^{[1]}X+b^{[1]})+b^{[2]}=W^{[2]}W^{[1]}X+W^{[2]}b^{[1]}+b^{[2]} = W^{‘}X+b^{‘}$
相当于经过多个隐藏层之后,结果还是输入的线性变化,那么隐藏层就没有意义了
只有一种情况使用线性激活函数,就是在做回归问题的最后一步的时候,输出值不是0和1而是一个实数,那么这个时候就应该使用线性激活函数,但是在中间的隐藏层仍然应该使用非线性激活函数。
激活函数的梯度下降
- sigmoid函数: $a=g(z)=\frac{1}{1+e^{-z}}$,导数是$g^{‘}(z)=g(z)(1-g(z))=a(1-a)$,在z=一个很大的正数或者负数的时候,g(z)导数接近于0;z等于0的时候,g(z)的导数是1/4
- tanh函数,$a=g(z)=\tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$,求导可得$g^{‘}(z)=1-g^{2}(z)$,我们可以通过一个简单的例子来检验有没有错误,当z很大或者很小的时候,$g^{‘}(z)=0$当,z=0的时候,导数=1
- Relu函数,$g(z)=max(0,z)$,导数=0(当$z<0$的时候),导数=1(当$z>=0$的时候)
- Leaky ReLU:$g(z)=max(0.01z,z)$,导数=0.01(当$z<0$的时候),导数=1(当$z>=0$的时候)
神经网络的梯度下降
左边是包含一个隐藏层的神经网络的推导公式,右边是反向传播求导的结果,其中np.sum函数中的keepdims=True这个参数是为了输出结果是(n,1)而不是(n,)
神经网络梯度下降的推导
从后往前推导,先求dz2=a2-y,因为L(a2,y)=-yloga-(1-y)log(1-a),对a求导,然后乘以sigmoid的导数刚好是a2-y,dw2=dz2a1T,这里的转置是通过维度来判断的,dw2一定和w2一样的维度,w2的维度是(n2,n1),那么dw2维度也是(n2,n1),dz2的维度与z2相同是(n2,1),那么应该右乘一个(1,n1)得到dw2,也就是a1T
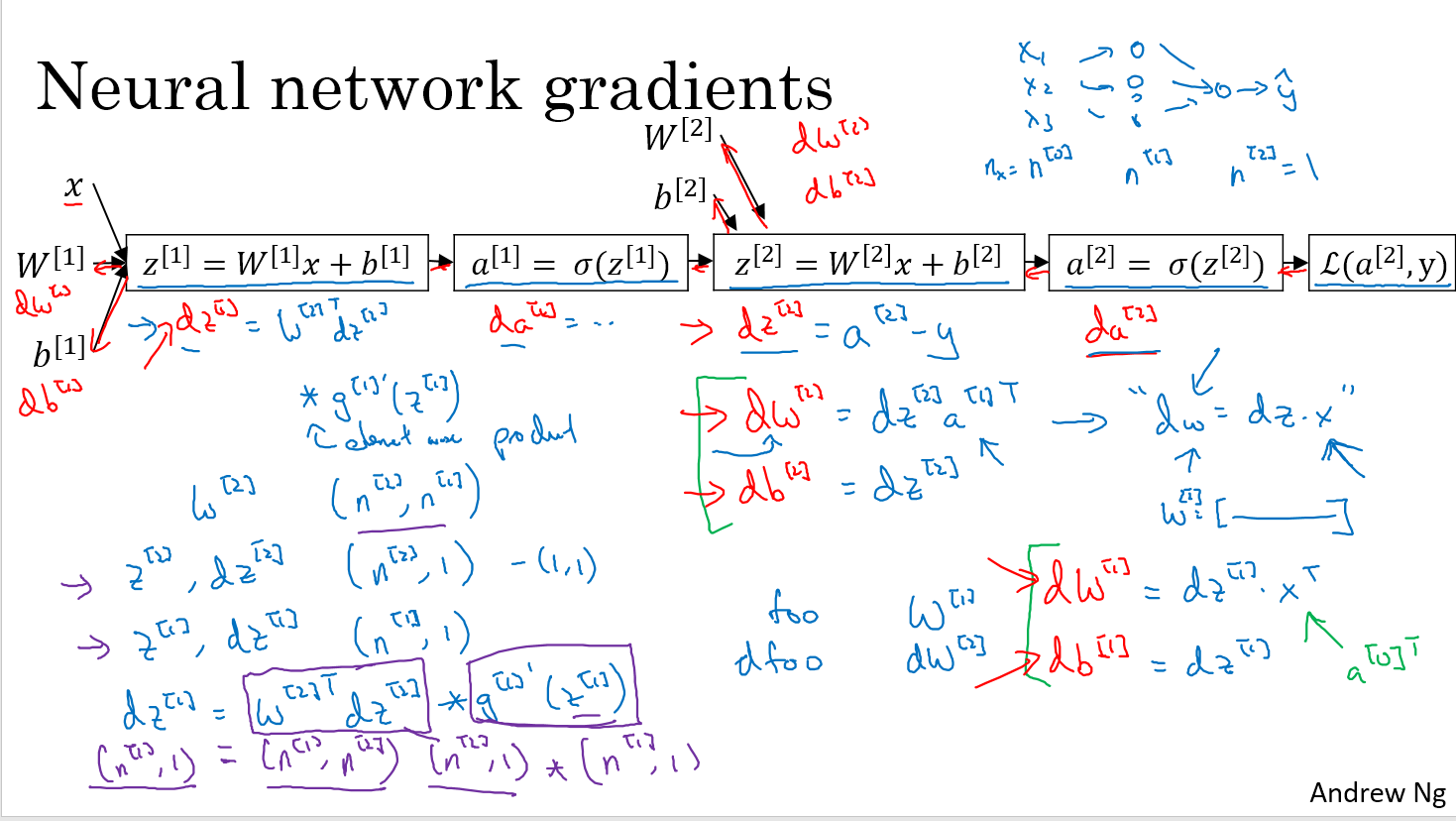
左边是一个输入的时候的梯度下降,右边是向量化之后多个输入的梯度下降,因为代价函数J前面有1/m,所以dw前面也有1/m,keepdims=True是为了保证b2的形状是(n2,1)

随机初始化
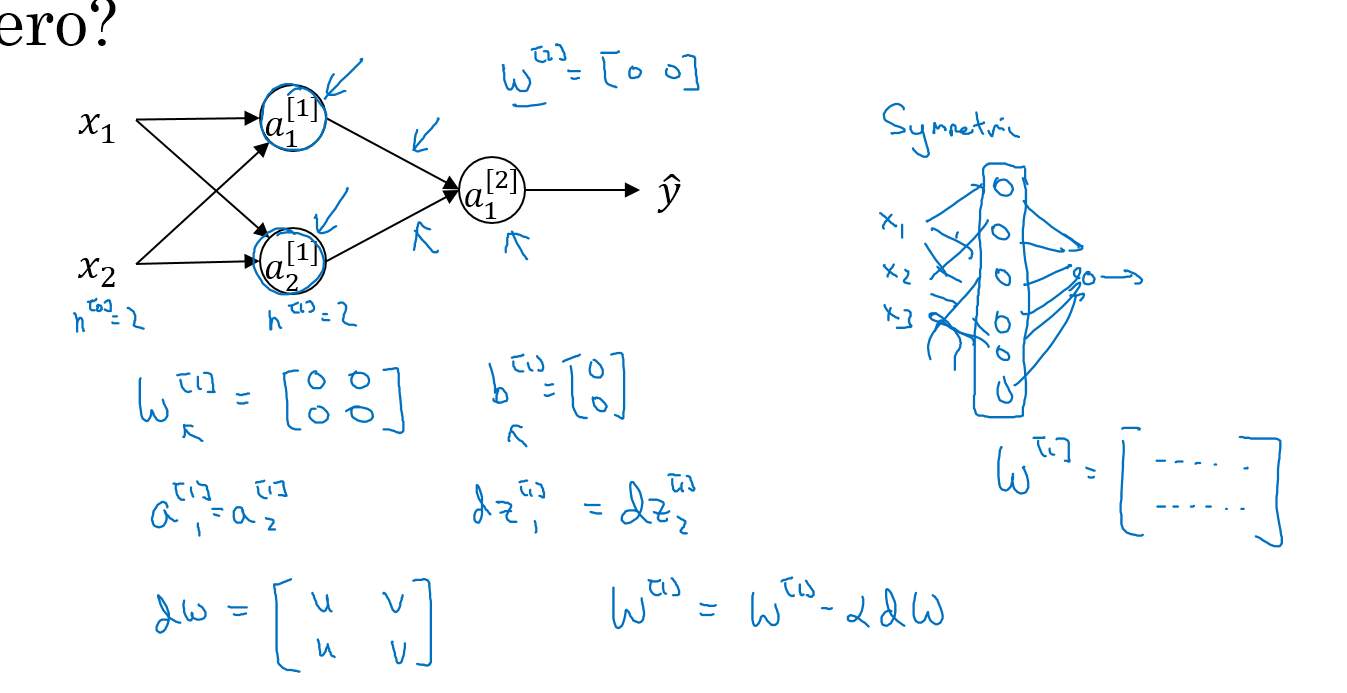
在逻辑回归中,w可以初始化为0,在神经网络中,我们必须要随机初始化w。这是为什么呢?主要是因为神经网络中存在隐藏层,如果一开始将w设置为全0,那么在反向传播的时候,通过$w = w-\alpha dw$这个公式进行迭代,每次迭代结束之后,两行的结果完全相同,这就是所谓的“对称”。这样多个隐藏点就跟1个隐藏点没有区别了
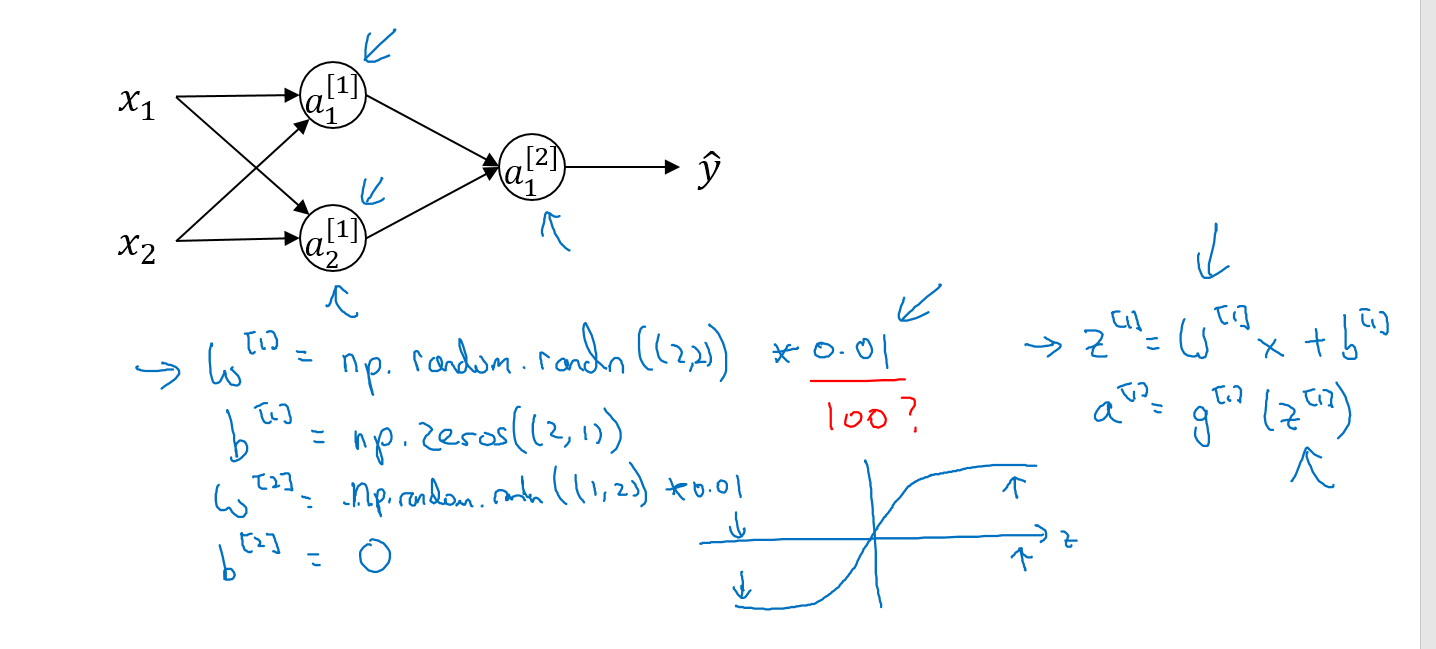
我们使用np.random.randn((1,2))随机初始化,并乘以一个很小的值,比如0.01,为什么不乘以一个很大的值比如100之类的呢,这是因为我们通常使用的激活函数,比如tanh和sigmoid函数,在值很大的时候斜率很小,迭代速度非常慢。
Week 4
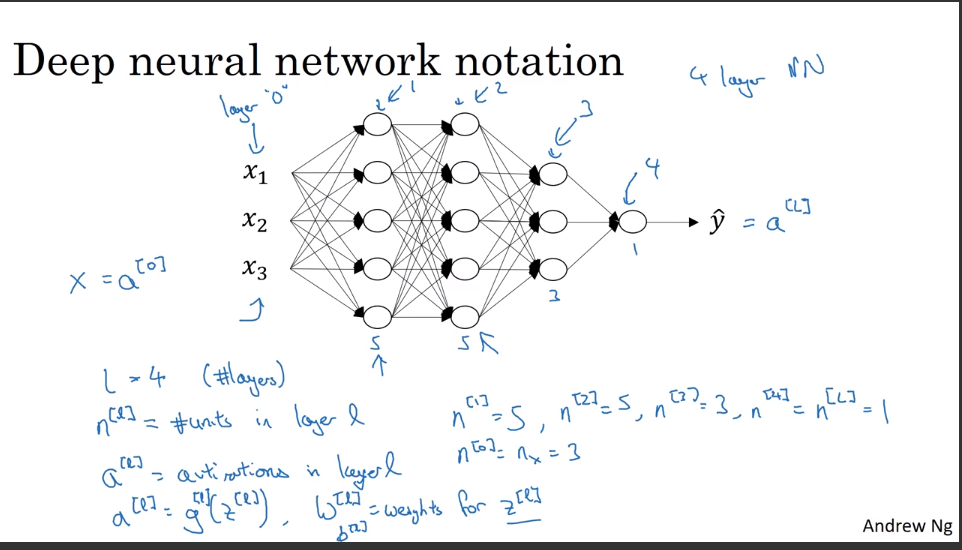
L层深度神经网络的符号表示
其中L表示神经网络的层数,不包括输入层,仅包含隐藏层和输出层,$n^{[i]}$表示第i层的点的个数
深度神经网络的前向传播
深度神经网络前向传播的通用公式:
$Z^{[l]}=W^{l}A^{[l-1]}+b^{[l]}$
$A^{[l]}=g^{[l]}(Z^{[l]})$
通过这个通用公式,我们就可以通过一个for循环,循环完所有的层
使矩阵维度保持正确
检查神经网络代码的最好的办法,就是拿出一张纸,看看矩阵维度是否正确
检查两个参数W,b和每层输出a和Z的维度
$W^{[l]}=dW=(n^{[l]},n^{[l-1]})$
$a^{[l]}=z^{[l]}=(n^{[l]},1)$
$b^{[l]}=db=(n^{[l]},1)$
矢量化之后的
$W^{[l]}=dW=(n^{[l]},n^{[l-1]})$
$A^{[l]}=Z^{[l]}=dA=dZ(n^{[l]},m)$
$b^{[l]}=db=(n^{[l]},1)$通过python的广播功能传播为$(n^{[l]},m)$
深度神经网络的解释
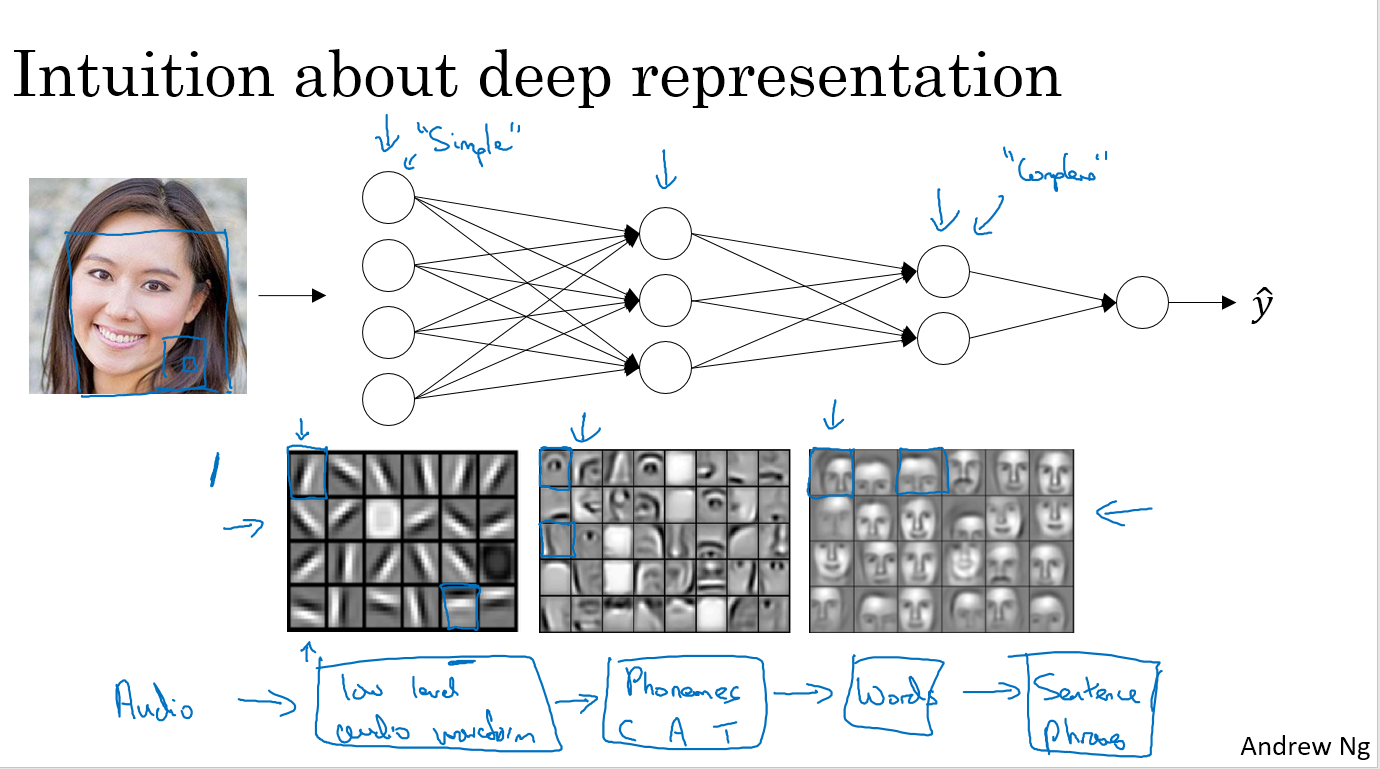
如下图,深度神经网络的第一层,可能能够检测一些图像的边缘,第二层可能由这些边缘组成了一些部件(比如人脸识别中的眼睛、鼻子、耳朵之类的),第三层再将这些眼睛鼻子耳朵之类的组合起来形成不同的脸,这就是神经网络的直观解释。
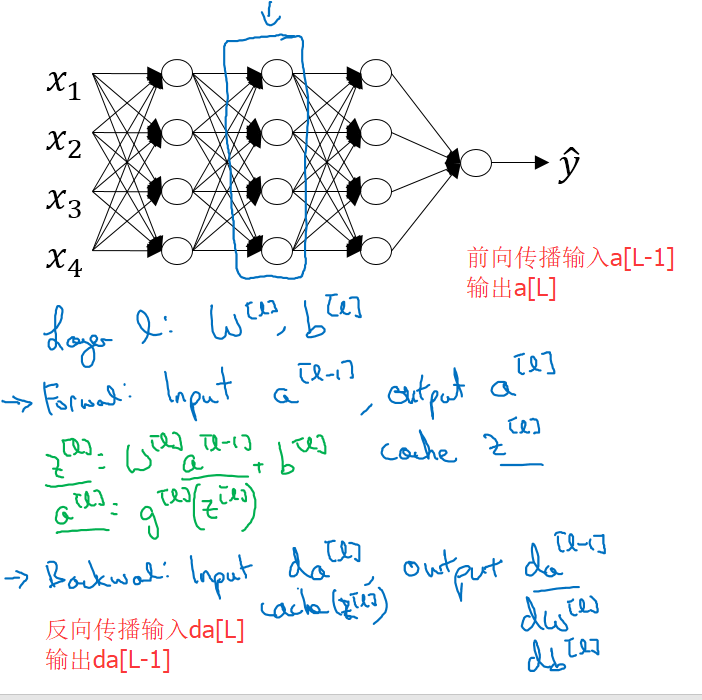
建立神经网络
神经网络主要分为两个部分,前向传播和反向传播
前向传播:输入$a^{[l-1]}$,输出$a^{[l]}$
反向传播中:输入$da^{[l]}$和$z^{[l]}$,输出$da^{[l-1]}$
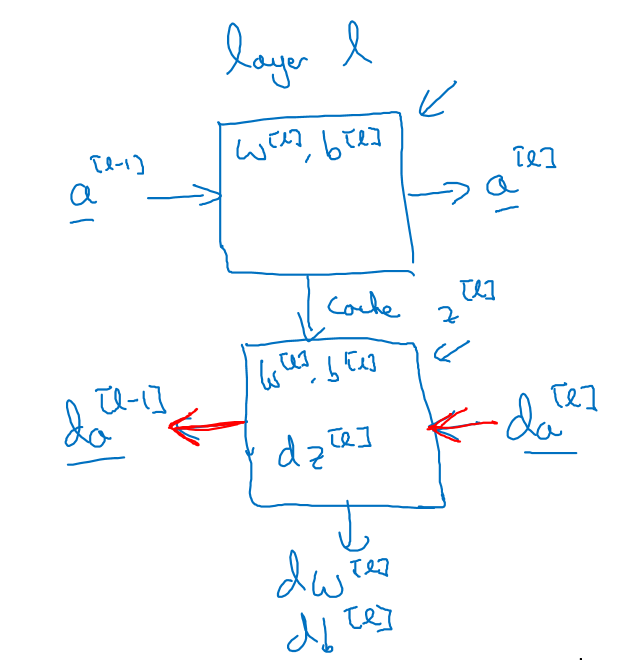
第L层的前向与反向传播示意如下:
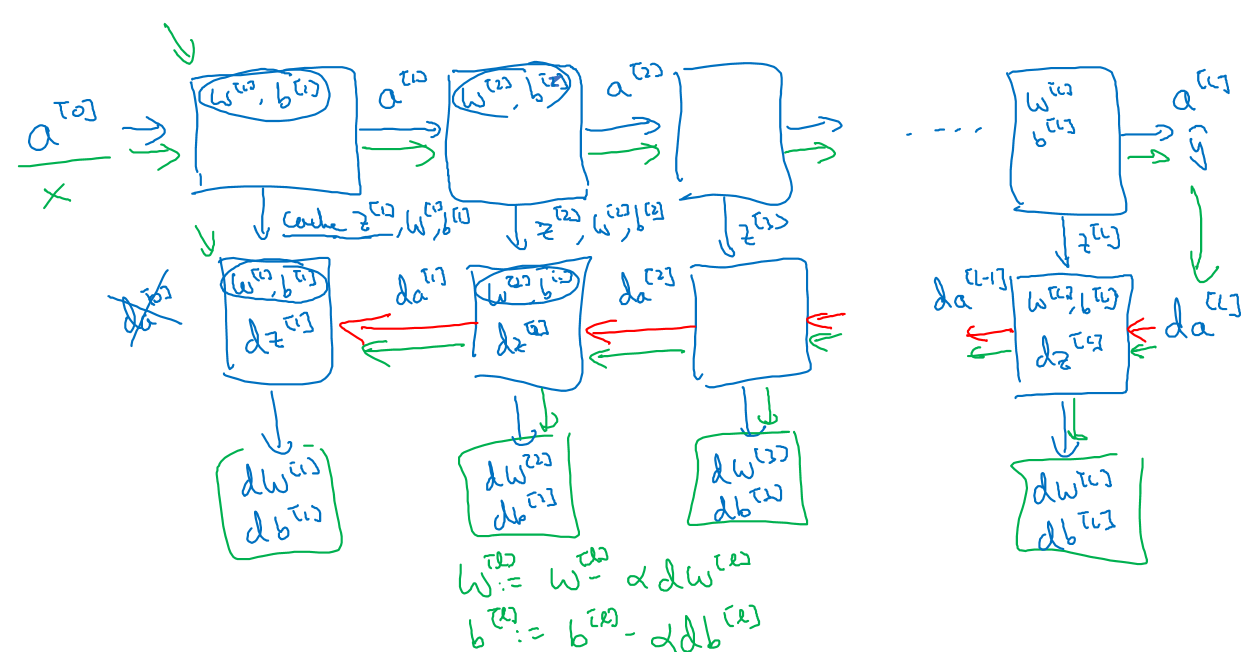
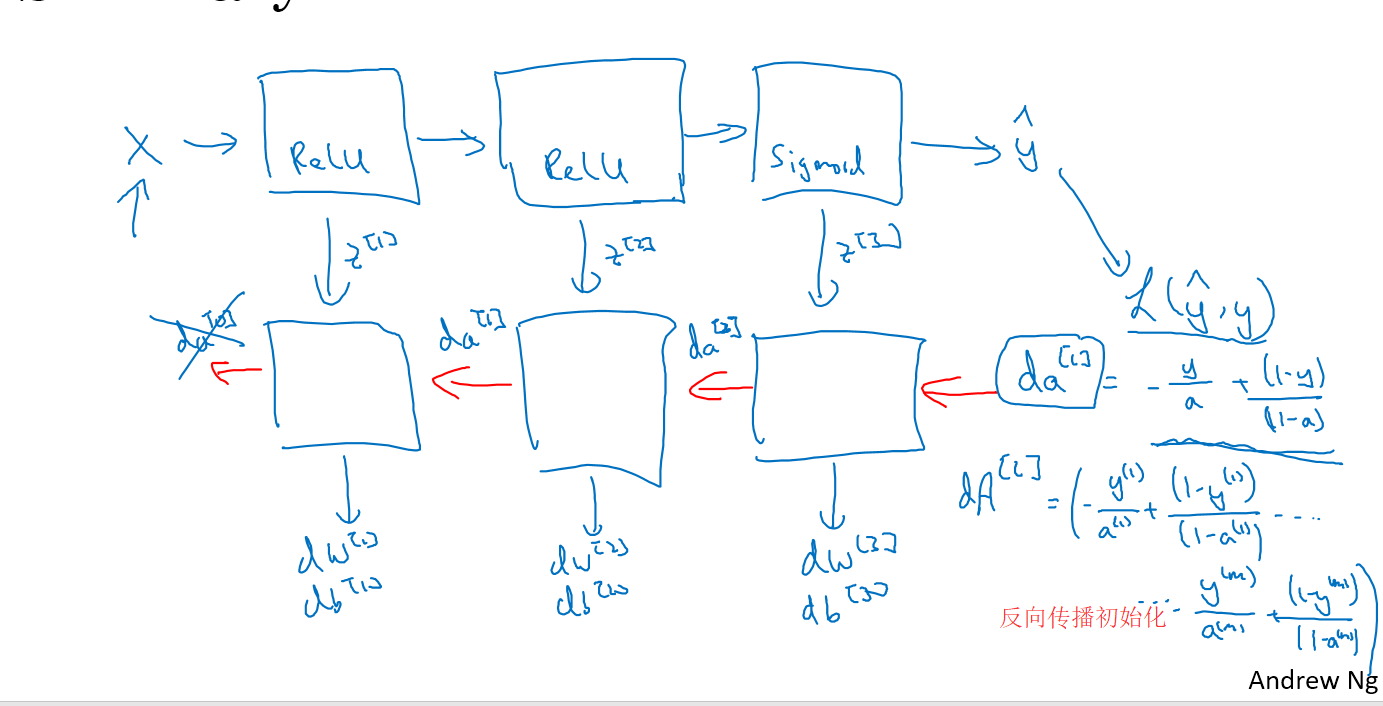
整个深度神经网络的传播示意如下:
先正向传播,再反向传播,算出dw和db后用更新公式更新w和b,就完成了一次迭代
正反向传播
第L层的正向传播
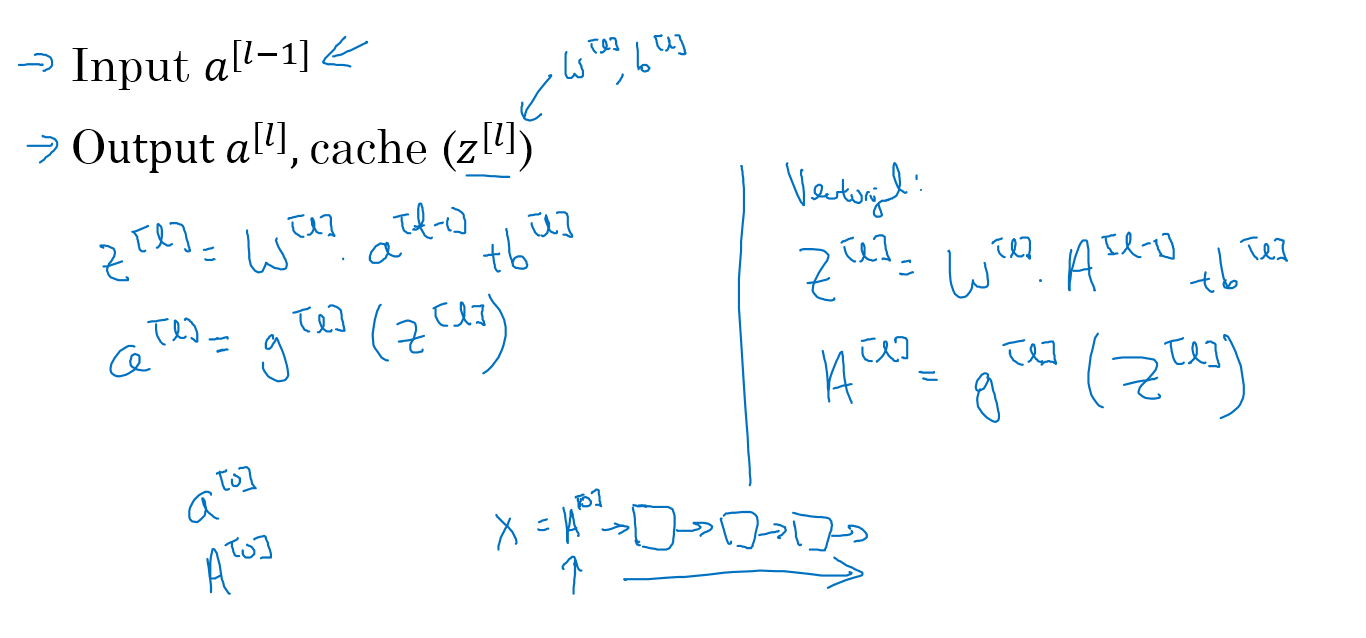
第L层的反向传播

前反向传播的总结
参数和超参数
神经网络中的参数:W,b
超参数:影响到实际的参数W和b的参数,比如学习率$\alpha$,迭代次数,隐藏层的个数,隐藏神经单元数,激活函数的选择(tanh,sigmoid,RELU)
一般都是不断的尝试找到最优的超参值(启发式搜索),比如学习率$\alpha$要找到一个下降较快,且算是函数收敛到较低的值。