具体来说可以分为五个部分:
- 问题理解
- 单变量分析
- 多变量分析
- 基本的数据清理
- 假设测验
首先导入过程中需要用到的python库
1 | import pandas as pd |
接下来读入数据:
1 | df_train = pd.read_csv('../input/train.csv') |
看一下每列都是些什么值
1 | df_train.columns |
得到如下的结果
1 | Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street', |
接下来我们需要做些什么
为了理解数据,我推荐用excel做一个如下的表格,每一列数据变成一类,包含6部分内容:
- 变量名;
- 变量类型:有两种可能的值在这个域中,“数值型”或者是“分类型”,数值型意味着数据都是数值,而“分类型”意味着变量值是类别;
- 变量分割:根据大类对变量分段。比如在房价问题中,可以大致分为3大类:“建筑本身”,“空间大小”,“位置”,当我们说建筑本身的时候,我们意味着建筑的物理特征;说空间大小的时候,指的是空间特征,比如有几个卫生间之类的;说位置的时候,指的是地理位置相关的特征,比如街区之类的;
- 期望:我们自认为的哪些因素对最终分析目标的影响,可以分为高中低三类。
- 结论:我们认为这个变量重要性的结论,可以跟期望一样分为几类
- 补充评论:任何我们能想到的一般性评论
最后,我们结合自身实际,看看哪些因素是真的重要的,比如买房子的时候,房子外观重要吗?
再看看哪些因素可能重复了,地势等高线之后就不需要地势斜度了
在房价预测这个问题中,我们总结了四个最重要的影响因素:
- OverallQual :整体质量,虽然不知道怎么算出来的,但是很有可能是通过其余所有变量综合计算得到的;
- YearBuilt:建筑年份
- TotalBsmtSF:总地下室面积
- GrLivArea:总的非地下室面积
在这个问题中,我们最终是以2个“建筑本身”变量(整体质量和建筑年份),和2个“空间大小”变量(地下室面积和非地下室面积)结束。
先说最重要的:分析房价
房价是我们这个问题探索的目标,首先看看数据描述
1 | #获得数据的整体性描述 |
1 | count 1460.000000 |
非常好,至少最低的房价是大于0的
1 | #画个直方图来看看数据分布 |
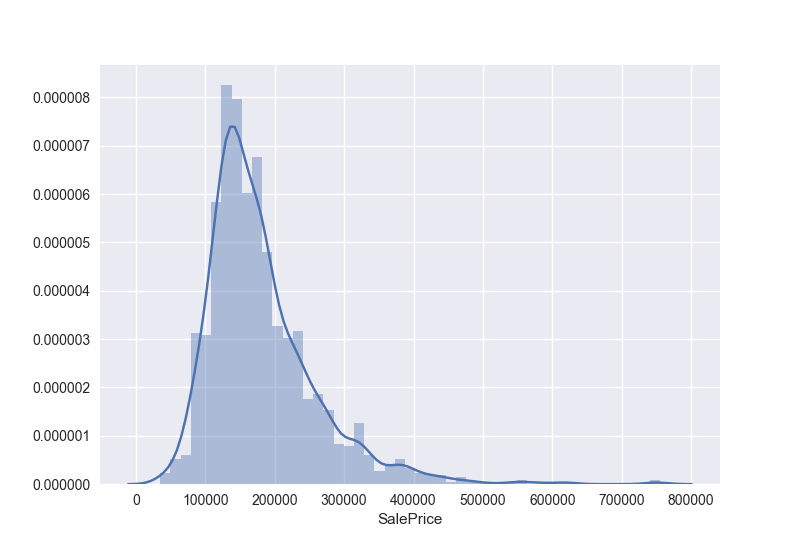
看上去似乎是一个变形的正态分布图片,我们来计算机下他的偏度和峰度:
1 | #skewness and kurtosis |
得到结果如下
1 | Skewness: 1.882876 |
其中峰度和偏度的解释如下:
- 峰度(skewness):峰度衡量数据分布的平坦度(flatness)。尾部大的数据分布,其峰度值较大。正态分布的峰度值为3

如图,黑线的峰度值大于3,红线峰度值等于3 - 偏态(Skewness):偏态量度对称性。0说明是最完美的对称性,正态分布的偏态就是0。如图所示,右偏态为正,表明平均值大于中位数。反之为左偏态,为负。

数值类型因素之间的关系
先来画一画grlivarea/saleprice两者之间的散点图
1 | #scatter plot grlivarea/saleprice |
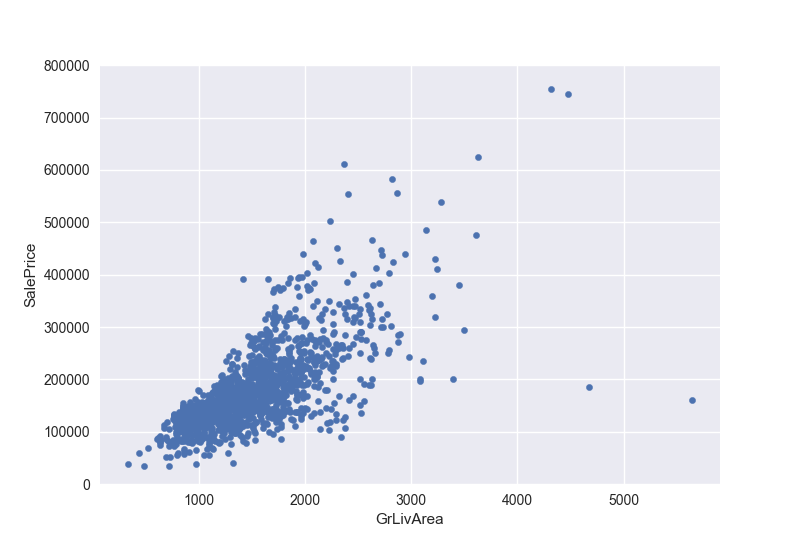
可以看到两者几乎呈现正相关,也就是非地下室面积和售价呈现正相关
我们再来画一下totalbsmtsf和售价的关系
1 | #scatter plot totalbsmtsf/saleprice |
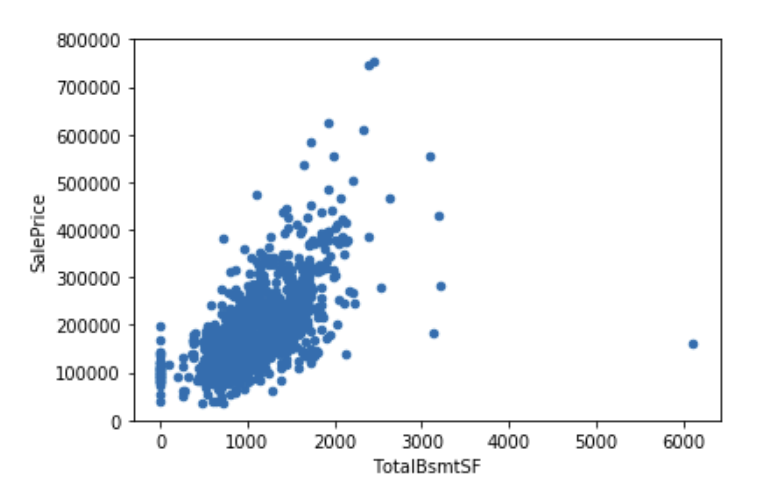
可以看到两者同样几乎呈现正相关,关系似乎是指数关系
分类类型变量的关系
画一个box图(箱形图),看看整体质量和售价之间的关系
1 | var = 'OverallQual' |
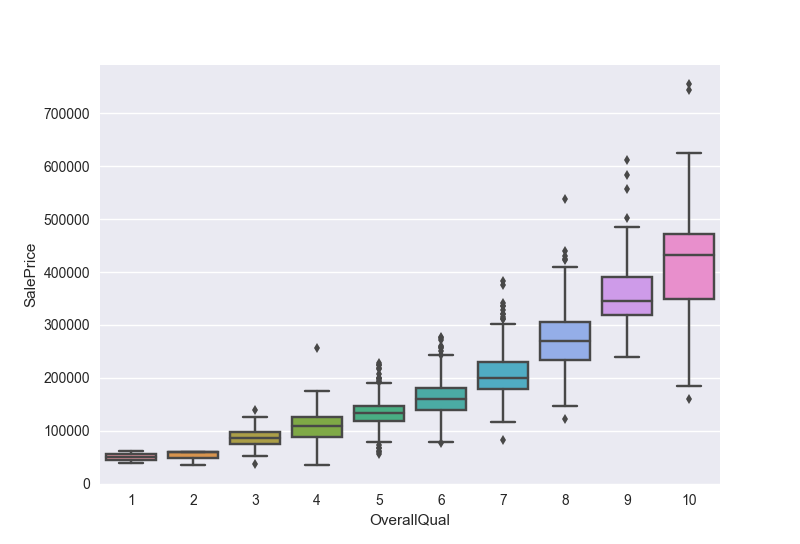
- 箱形图的解释:又称为盒须图、盒式图、盒状图或箱线图,是一种用作显示一组数据分散情况资料的统计图。因型状如箱子而得名。在各种领域也经常被使用,常见于品质管理。不过作法相对较繁琐。它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。
- 上四分位数Q3-下四分位数Q1 = 四分位间距$\Delta{Q}$
- 在区间$Q3+1.5\Delta{Q}$和区间$Q1-1.5\Delta{Q}$之外的值应该被忽视,被称为异常值,异常值被画在图上
再看看建造年份和售价的关系
1 | var = 'YearBuilt' |
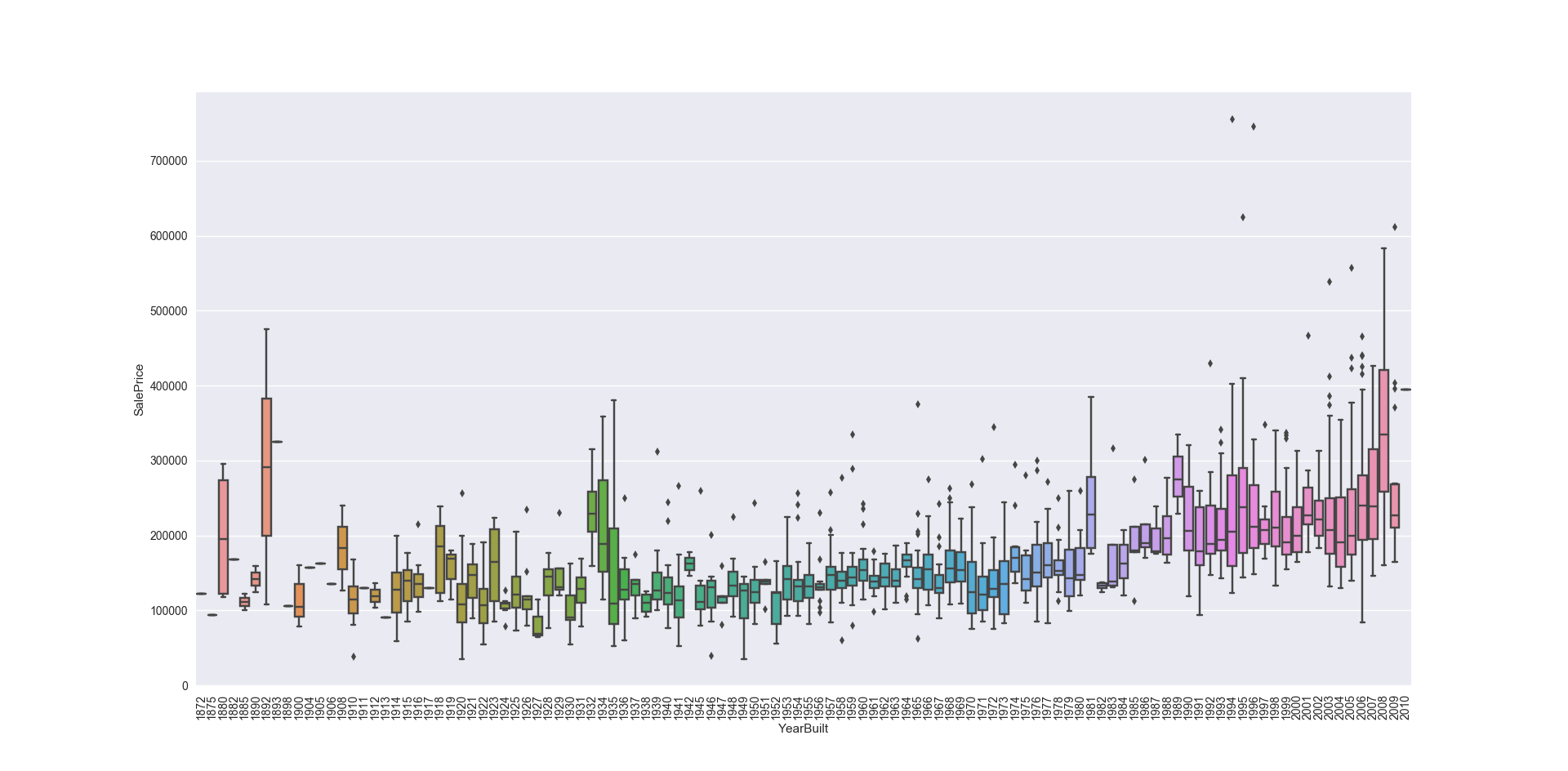
看上去似乎并没有什么强烈的关系
关系总结
- 地上面积和总的地下面积看上去和房价线性相关,两者的关系都是正向的;并且在总地下面积的关系中可以看到,其与售价面积相关性的斜度非常大
- 总体质量和建筑年代似乎与售价也有一定关系,其中总体质量关系比较大,箱形图显示出房价随着整体质量的上升而上涨
试验性分析
为了更加理性的对房价数据进行分析,我们先用一下几个办法来进行分析:
- 相关矩阵(热力图heatmap)
- 房价的相关矩阵(缩放热力图)
- 大多数相关变量之间的散点图
相关矩阵
画个热力图看看相关系数
1 | cormat = train.corr() |
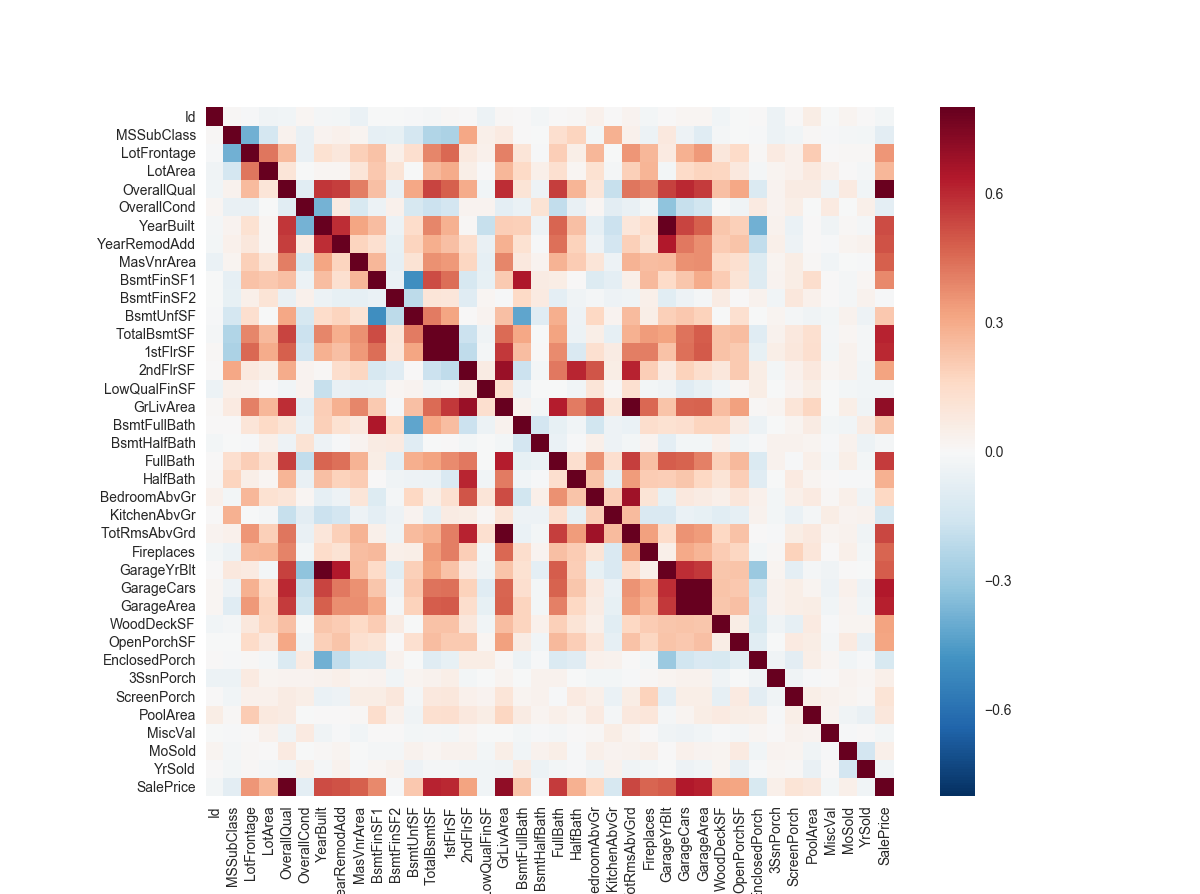
在我看来,热力图的确是一个最好的看一个大致影响程度的方法。
可以看到,总地下室面积和一楼面积很大程度上影响了房价,还有关于车库的好几个因素都很大程度上影响了房价。这让我们感觉到heatmap非常适合做特征选择。
售价相关矩阵
看完了上面的heatmap的最后一行,我们只是从颜色上看出了各个因素与售价的关系,接下来我们画一个缩放的heatmap来具体看看每个因素的影响有多大
1 | cormat = train.corr() |
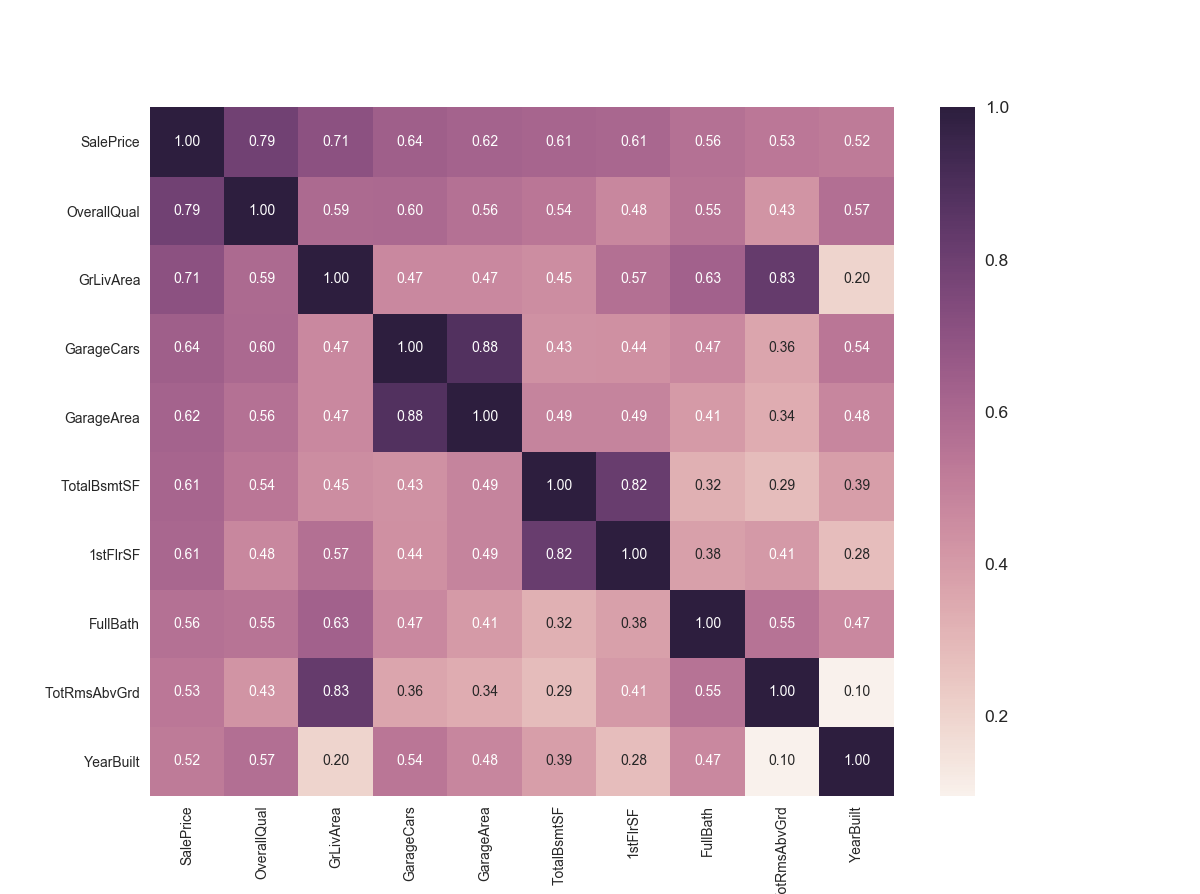
可以看到这些变量是影响房价最大的10个因素,从图中的数值可以看出来,OverallQual和GrLiveArea以及GarageCars和GarageArea是影响房价最大的几个因素。
- 然而我们可以看到,GarageArea和GarageCars是有因果关系的,车库面积决定了可以停多少车,所以我们最终选择影响更大的GarageCars这个因素
- 总地下室面积(TotalBsmtSF)和一楼面积1stFlrSF似乎也有强烈相关性,我们选择地下室面积作为因素
- 地上房间数目(TotRmsAbvGrd)和地上居住面积(GrLivArea)也有相当大关系,所以选其中一个
售价和相关变量之间的散点图
1 | #画出所有与售价相关的10个因素之间的关系图pairplot |
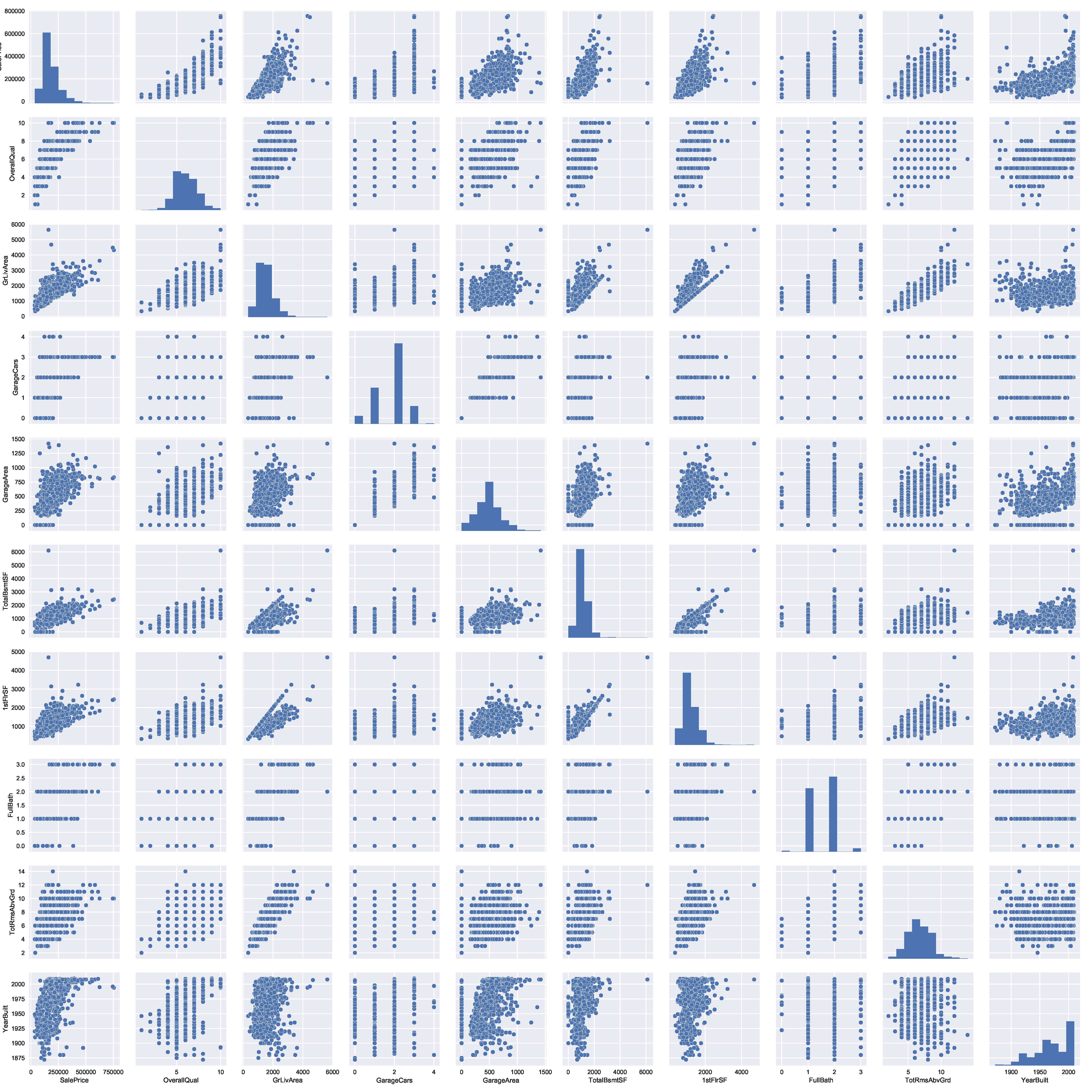
大量的散点图给了我们一个变量之间关系的合理解释
缺失数据的处理
在处理缺失数据之前不妨问一下以下两个问题:
- 缺失数据的比例有多大
- 缺失数据是随机的吗还是说缺失数据有一定的模式
这两个问题非常重要,因为缺失数据可能就意味着训练数据的减少,对我们的分析不利。
先来找到缺失的数据:
1 | #isnumll()函数将返回与原dataframe同样形状的dataframe,不过原来为空的地方标为1,原来不为空的地方标0 |
得到如下的结果
| total | percent | |
|---|---|---|
| PoolQC | 1453 | 0.995205 |
| MiscFeature | 1406 | 0.963014 |
| Alley | 1369 | 0.937671 |
| Fence | 1179 | 0.807534 |
| FireplaceQu | 690 | 0.472603 |
| LotFrontage | 259 | 0.177397 |
| GarageCond | 81 | 0.055479 |
| GarageType | 81 | 0.055479 |
| GarageYrBlt | 81 | 0.055479 |
| GarageFinish | 81 | 0.055479 |
| GarageQual | 81 | 0.055479 |
| BsmtExposure | 38 | 0.026027 |
| BsmtFinType2 | 38 | 0.026027 |
| BsmtFinType1 | 37 | 0.025342 |
| BsmtCond | 37 | 0.025342 |
| BsmtQual | 37 | 0.025342 |
| MasVnrArea | 8 | 0.005479 |
| MasVnrType | 8 | 0.005479 |
| Electrical | 1 | 0.000685 |
| Utilities | 0 | 0 |
看一看到缺失最多的达到了99.5%,我们现在制定一个原则,当数据缺失超过15%的时候,我们就把这个变量删掉
同样,虽然Garage相关的数据只缺失5%,但是“GarageCars”已经可以表示车库相关的问题,我们把garage相关的信息删掉,同样BsmtX相关的变量也删掉
最后,我们的删除方案是,除了只有一个缺失值的Electrical列删除缺失值所在行,别的都删除所在列
1 | train = train.drop((miss_data[miss_data['total'] > 1]).index,1) |
异常值处理
异常值会对模型产生很大的影响,因此需要格外注意
单变量分析
这里最主要的问题就是建立一个阈值去筛选出异常值,因此我们需要对数据进行标准化。意味着将数据值变化到均值为0,标准差为1的数据
1 | # 标准化数据 |
找到标准化之后数据的最大最小的10个值
1 | lowrange = np.sort(saleprice_scaled)[:10] |
得到结果
1 | [-1.83820775 -1.83303414 -1.80044422 -1.78282123 -1.77400974 -1.62295562 |
可以看到,最小值都比较相近且接近0,最大值相差比较大,且远离0,特别是有几个7点几的几乎可以肯定是异常值
二元变量分析
我们画出地面居住面积和房价的散点图
1 | # 二元分析房价与地上居住面积 |
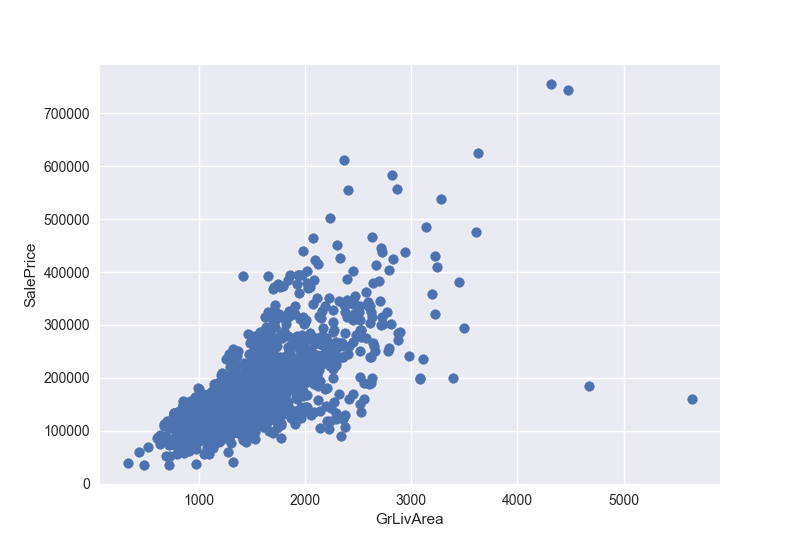
- 有两个面积很大但是价格很低的点,我们可以推断他们对我们的分析意义不大,可能是偏远农村的房子。我们认为这两个点是异常值并删除他们。
- 最高处的两个点,应该就是我们在标准化数据的时候得到的7点几的两个点,然而他们两个点好像符合这个线性关系,我们暂时决定保留他们。
我们先删除两个异常值
1 | # 删除异常值 |
得到:
1 | 删除之前的矩阵:(1459, 63) |
接下来进行售价和总地下室面积的二元分析
1 | var = 'TotalBsmtSF' |
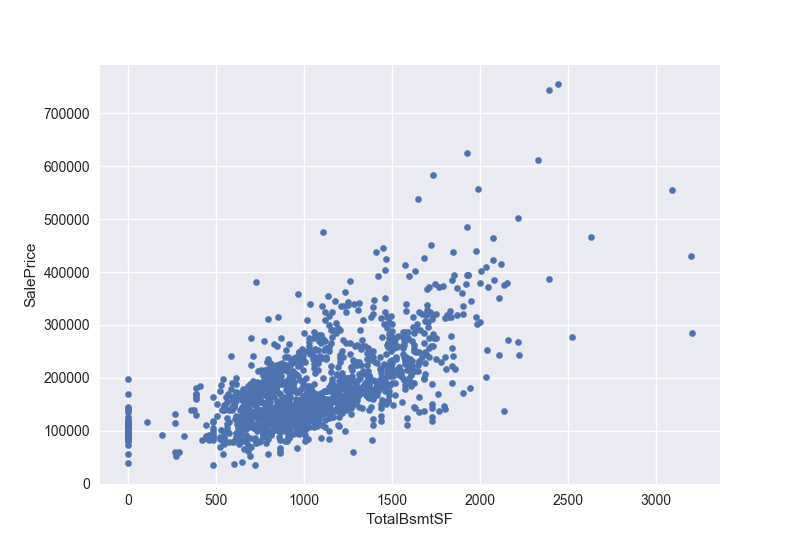
我们可能很想要删除那几个居住面积大于3000的值,但是在这里我们先保留他们
得到模型
我们已经完成了数据清理,现在需要对售价的模型提出假设:
根据论文Hair et al. (2013)中提到,我们需要对数据进行四类假设:
- 正态性:说到正态性就是说数据长得比较像正态分布,这非常重要,因为好几种统计测试方法都依赖于这个(比如t-statistics)。在这个问题中我们只是检查售价这个单变量的正态性,记住:单变量的正态性并不意味着多变量的正态性,还有,在样本超过200的时候,正态性并不是个问题。如果我们解决了正态性,那么就避免了很多别的问题,比如heteroscedacity(异方差),这个就是我们为什么要做这个分析的原因,
- 同方差性:所有自变量的方差相同
- 线性:最好的检查现行的方法就是画散点图,看看上面有没有直线。
- 相关误差的缺乏:相关误差是在一个误差发生的时候,与其相关联的值也会发生误差。
寻找正态性
我们之前已经看了房屋售价的histgram的图,找到了峰度和偏态。
那么我们再画一个正态概率图,用来找到我们的histgram和正态分布的区别
1 | sns.distplot(train.loc[:,'SalePrice'], fit=norm) |
得到下面两张图
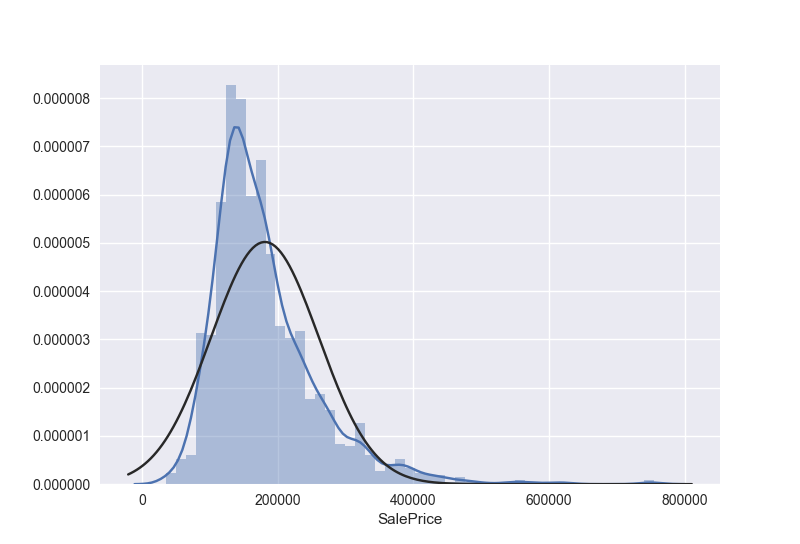
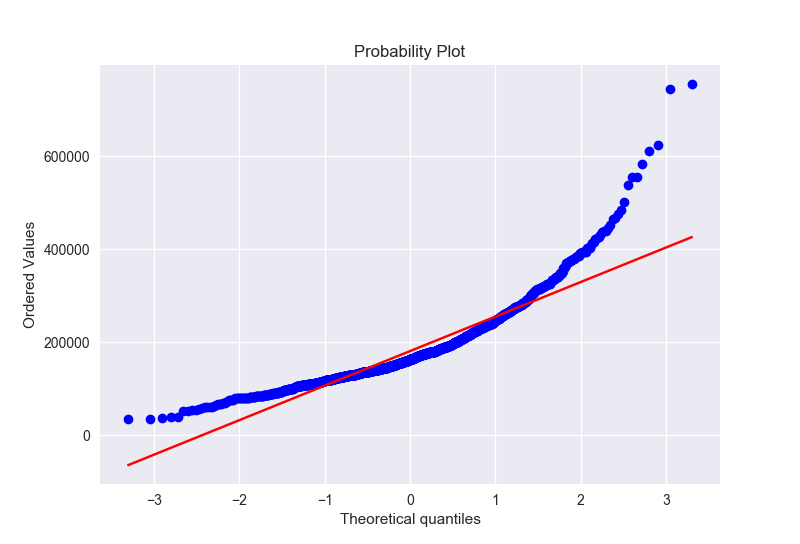
显然,售价并不是正态分布,他有一个尖峰,并且正的偏度。然而我们可以通过一个简单的变换把这些数据变成正态的,在统计学中可以知道,当数据分布是有正的偏度的时候,log变换非常有效。
进行log变换
1 | train['SalePrice'] = np.log(train['SalePrice']) |
变换之后的数据
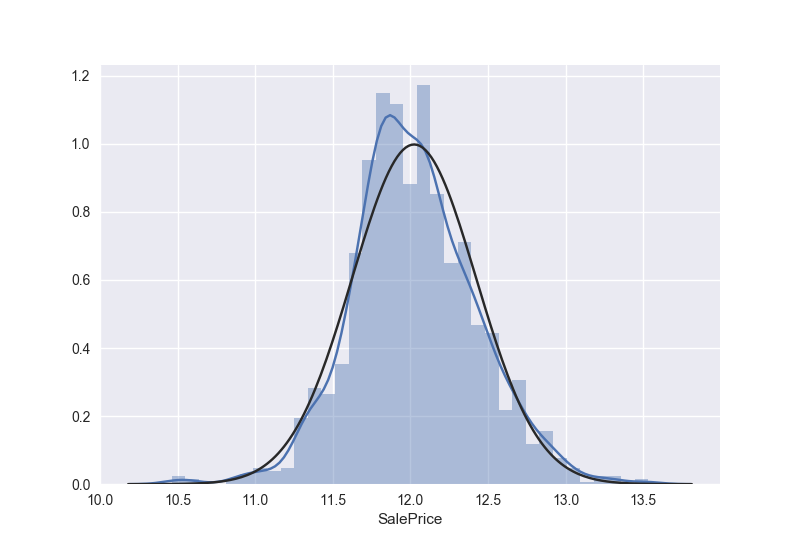
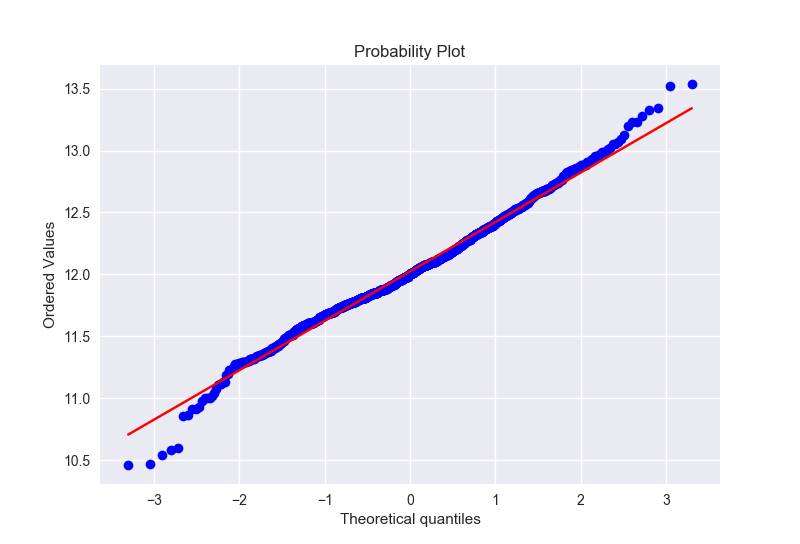
同样,我们对GrLivArea进行一个log变换
1 | train['GrLivArea'] = np.log(train['GrLivArea']) |
得到变换之后的图形如下:
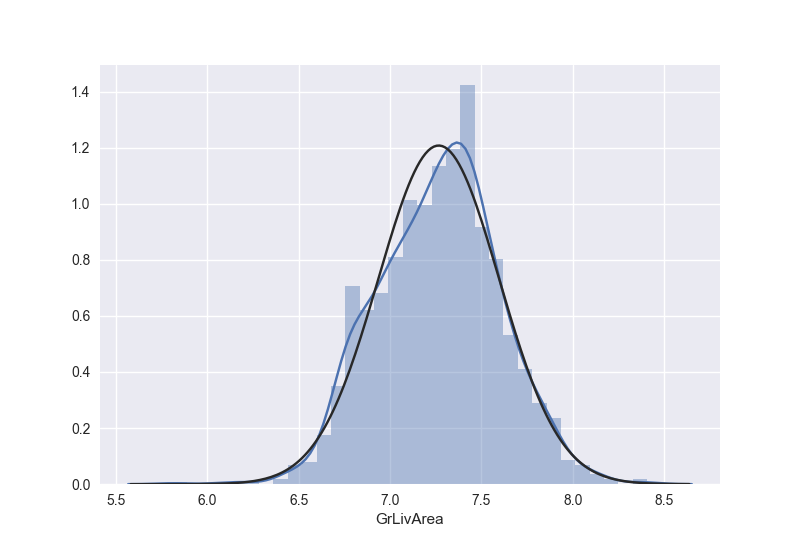
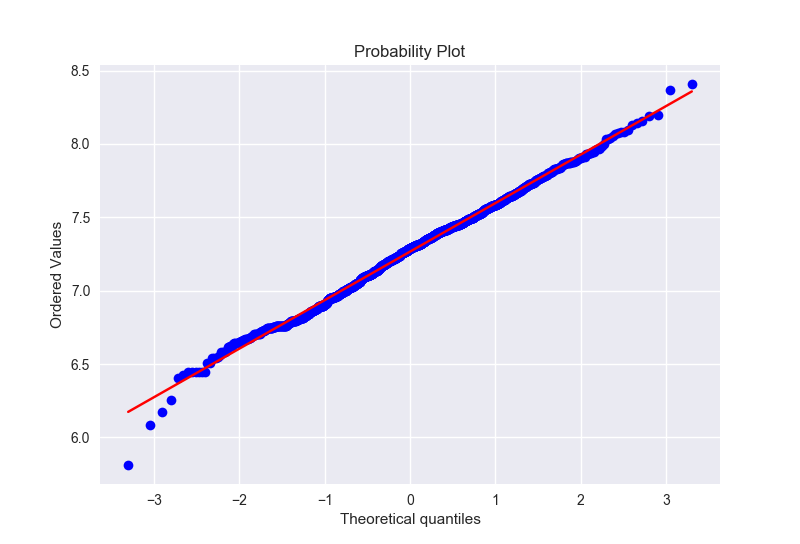
我们再来看看TotalBsmtSF本来的数据长什么样子:
1 | sns.distplot(train['TotalBsmtSF'], fit=norm) |
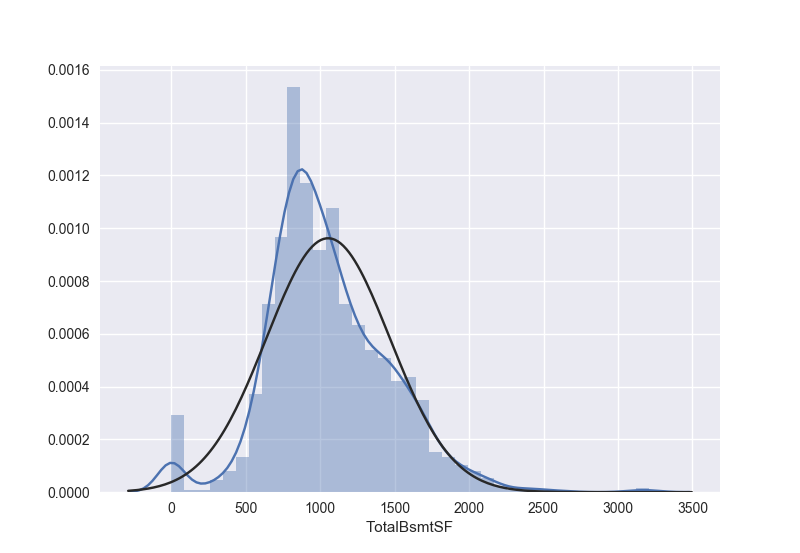
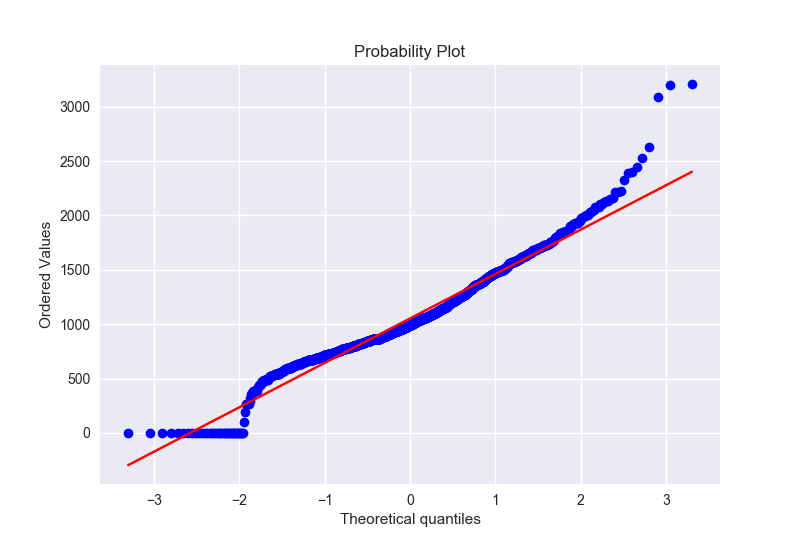
- 我们可以看到好多值都是0,这样我们就不能用log变换了
- 我们在做log变换之前需要把所有为0的值变为1,这样变换之后,值还是0
1 | print('等于0平的地下室',train[train['TotalBsmtSF'] == 0]['TotalBsmtSF'].shape) |
我们只画出为正的那部分的地下室的变化之后的分布,也服从正态分布
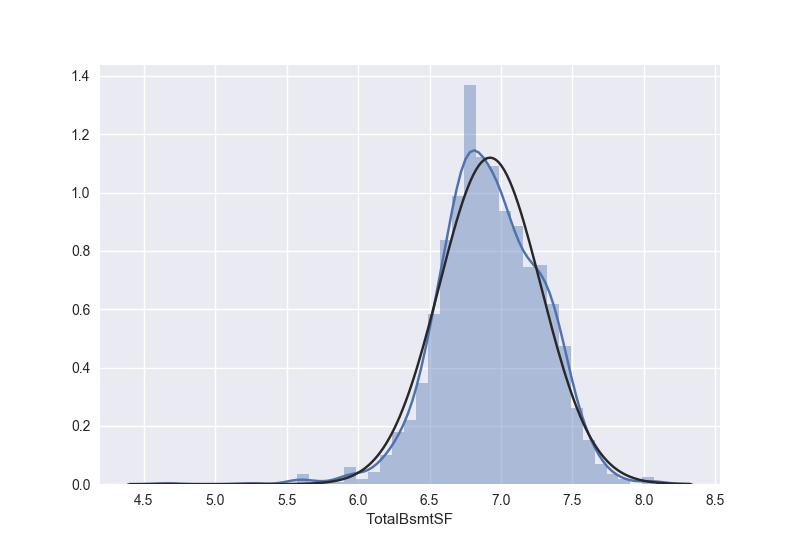
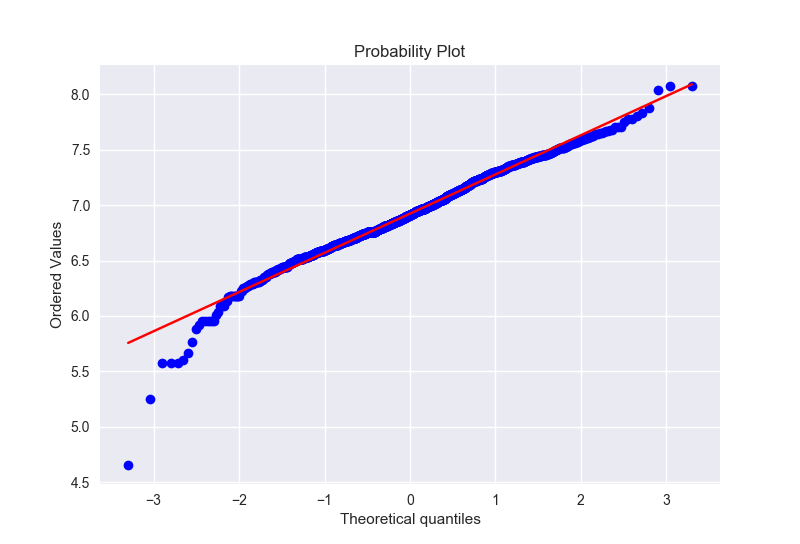
验证同方差性
最好的验证同方差性的办法就是图形。
先看看‘SalePrice’ and ‘GrLivArea’的分布
1 | plt.scatter(df_train['GrLivArea'], df_train['SalePrice']) |
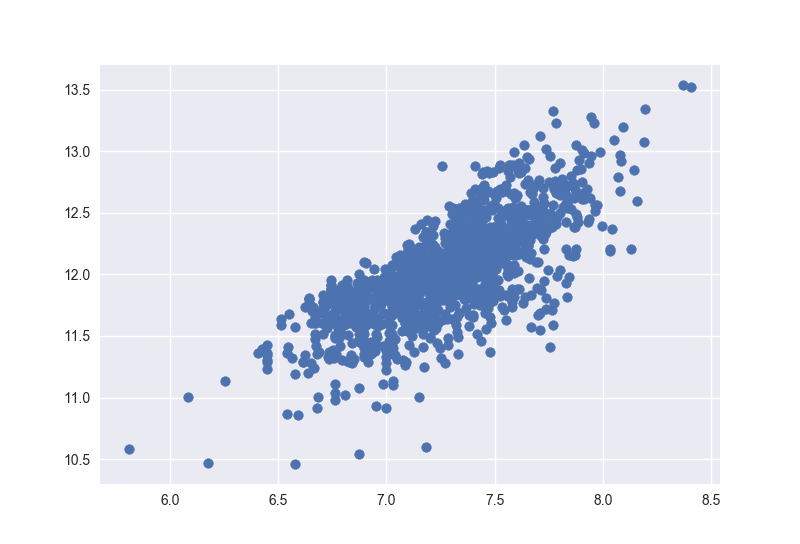
对比log变化之前的图形,可以看到这个图没有之前那种锥形的样子了,这就是正态性的效果,确保了正态性往往就确保了同方差性
再看看’SalePrice’ with ‘TotalBsmtSF’.
1 | plt.scatter(train[train['TotalBsmtSF']>0]['TotalBsmtSF'], train[train['TotalBsmtSF']>0]['SalePrice']); |
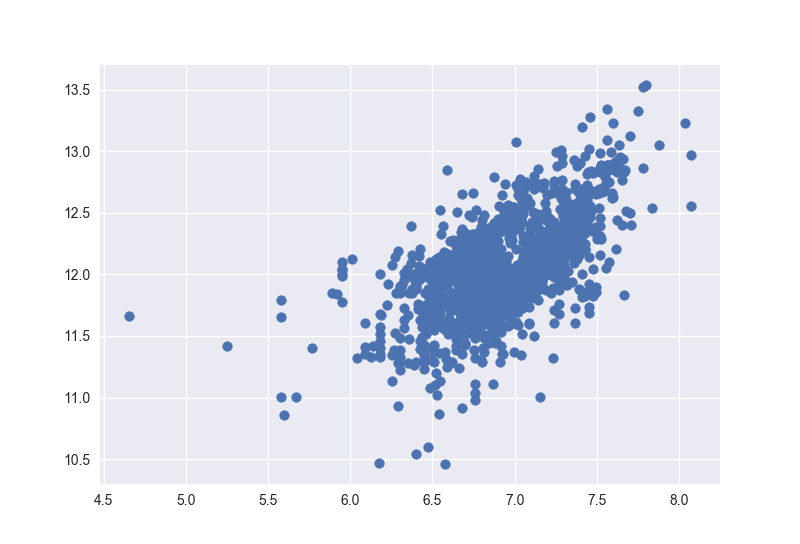
哑变量
1 | df_train = pd.get_dummies(df_train) |
一句话就可以推出哑变量