离春招开始的时间已经不久了,因此最近开始在工作之余看看剑指offer这本书,了解更多关于算法相关的知识。
第一章主要是介绍面试流程等,该篇博文主要讲述从第二章开始的编程知识相关的内容。
第二章
c++
对空类型求sizeof,结果是多少?
答:答案是1,本来应该是0,但是声明实例的时候,必须在内存中占有一定的空间,占多少内存由编译器决定。在visual studio中,每个空类型实例占用1字节的空间如果添加构造函数和析构函数,再求sizeof的结果是多少?
答:还是1,因为调用构造函数和析构函数只需要知道函数的地址即可,函数地址与类型相关,而与类型的实例无关,编译器不会因为这两个函数在实例内添加任何额外的信息。
如果把析构函数标记为虚函数呢?
答:c++中一旦出现虚函数,就会为该类型生成虚函数表,并在每个实例中添加一个指向虚函数表的指针。在32位机器上一个指针占用4字节,因此结果是4;在64位机器上一个指针占用8字节,因此结果是8.
给出下面代码的运行结果
1 | class A{ |
结果是编译错误,原因是因为在第二个构造函数中,用了一个实例来初始化另外的实例,但是c++函数的值传递过程中,是需要复制参数为形参的,复制参数位形参的过程就需要调用构造函数,那就相当于在调用构造函数的过程中需要调用构造函数,因此陷入递归调用,编译报错。
要解决这种问题,我们可以使用引用参数传递,这样不会复制参数,就不会报错,构造函数修改为A(const A& other)
面试题1:赋值运算符函数
定义如下类型,要求重写他的等号赋值运算符
1 | class CMyString{ |
要考四个方面:
- 只有返回一个引用才可以连续赋值,否则str1=str2=str3这种赋值将无法通过
- 传入参数是否声明为引用,如果传入参数是引用就不用复制参数,这样能提高代码效率,如果不改变传入实例的状态,应该在传入的引用参数之前加入const
- 是否释放自身内存,如果在分配新内存之前释放自身空间,则程序将出现内存泄漏
- 判断传入的参数和当前的实例是不是同一个实例,如果是同一个实例,不赋值,直接返回。如果不判断,在释放自身内存的时候,就把赋值的对象给释放了。
经典解法:
1 | CMyString& CMyString::operator=(const CMyString& str){ |
数据结构
常用的数据结构必须掌握:数组,字符串,链表,树,栈,队列
其中数组和字符串是两种最基本的数据结构
数组
数组内存连续,因此可以在O(1)时间内读写任何元素,时间效率很高,因此可以用来实现简单的哈希表,数组下标设为哈希表的key,数组中的数字设为value,形成键值对。
数组空间效率不高,因为一旦你定义了数组,那么整个数组占用的内存空间就无法被利用,因此STL中定义了vector这种动态数组,一开始分配一个小空间,每次往里面添加元素,当空间不够的时候,新开辟一块内存空间,大小是原来的2倍,把数据拷贝过来,并释放原先的内存空间。
数组与指针
c/c++中,数组的名字也是一个指针,指向数组的第一个元素
1 | int GetSize(int data[]){ |
上述结果为:
1 | size1:20 |
因为数组每一个元素占4个字节,5个元素的数字就是20个字节
指针data2虽然指向数组data1,但是其本身还是个指针,因此sizeof(data2)结果是8(64位系统一个指针占8个字节,32位系统一个字节占4个字节)
在GetSize函数的情况中,data1通过参数传入函数,数组自动退化为指针,因此结果为一个指针的大小8;
面试题3:查找数组中的重复的数字
在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复的次数。请找出数组中任意一个重复的数字。例如如果输入长度为7的数组{},那么对应的输出是重复的数字2或者3。
解答:解决这个问题最简单的方法就是先排序,然后从头到尾扫描数组,如果第i个值与第i+1个值相等则有重复,排序一个长度为n的数组的时间复杂度是O(nlogn),下面是为什么排序算法的复杂度是O(nlogn)
a1,a2,a3……an排序总共有n!总结果,(其中a1’<=a2’<=a3’……<=an’)所占的概率是1/n!,每进行一次比较,就是在这n!种结果中进行二分,接着选择一个二分结果进行下一次二分,直到找到想要的排序。排序算法能不能自顶向下构造出一棵决策树?因为我们讨论的是基于输入元素的比较排序,每一次比较的返回不是0就是1,这恰好可以作为决策树的一个决策将一个事件分成两个分支。比如冒泡排序时通过比较a1和a2两个数的大小可以把序列分成a1,a2……an与a2,a1……an(气泡a2上升一个身位)两种不同的结果,因此比较排序也可以构造决策树。根节点代表原始序列a1,a2,a3……an,所有叶子节点都是这个序列的重排(共有n!个,其中有一个就是我们排序的结果a1’,a2’,a3’……an’)。如果每次比较的结果都是等概率的话(恰好划分为概率空间相等的两个事件),那么二叉树就是高度平衡的,深度至少是log(n!)。又因为log(n!)的增长速度与 nlogn 相同,即 log(n!)=Θ(nlogn),这就是通用排序算法的最低时间复杂度O(nlogn)的依据。
证明log(n!)=Θ(nlogn)等价于证明①、②
①log(n!)=O(nlogn)
显然n!<n^n,两边取对数就得到log(n!)<nlog(n)。②log(n!)=Ω(nlogn)
n!=n(n-1)(n-2)(n-3)…1,把前n/2个因子(都大于n/2)全部缩小到n/2,后n/2个因子全部舍去,得
n!>(n/2)^(n/2)。两边取对数,log(n!)>(n/2)log(n/2),后者即Ω(nlogn)。
第二个方法是利用一个哈希表,每扫描到一个数字,如果哈希表里面没有这个数字,就把他加入哈希表,如果已经有该数字,那么就找到了重复的数字,此方法的时间复杂度为O(n),但是提高时间效率的方法是以一个O(n)大小的哈希表为代价的,再看看有没有空间复杂度为O(1)的算法
因为数字都在0~n-1范围内,如果数组中没有重复的数字,那么排序后i这个数字应该出现在第i个位置,从头到尾扫描数组,扫到第i个数字,比较当前数字m与下标i是否相等,是则扫描下一个数字,否则交换m个和第m个元素。
1 | def get_duplicate(lists): |
java版本:
1 | public static int dupNum(int[] nums){ |
在一个长度为n+1的数组里的所有数字都在1~n的范围内,所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字,但是不能修改输入的数组。例如,如果输入长度为8的数组{2,3,5,4,3,2,6,7},那么对应的输出是重复的数字2或者3。
解答:与上一题很像,但是题目要求不能修改数组,因此不能用上一题最后一个方法。同样这道题可以用一个大小为n的辅助空间。
接下来尝试使用避免O(n)辅助空间的方法,那就是二分法。既然所有数字都在1
n之间,如果有重复的数字,那么这个重复数字要么在1n/2之间,或者在(n+1)/2n之间。将1-n通过中间值m分成两部分:1m和m+1~n,判断在哪个区间的方法就是判断区间中数字的数量和区间长度,如果数量小于区间长度,那么证明重复值不在当前区间,反之则反之,判断数字的数量的方法就是遍历一遍数组。这样不停地分下去,直到区间的start和end相等的时候,如果这个值出现的次数还是>1,那么这个值就是重复的值。二分查找有个问题就是:不一定能找到所有重复的数字,比如{2,2,3,4}这样一个数组,二分之后1,2之间值的个数是2,不会认为这个区间有重复
1 | # 方法1 |
面试题4:二维数组中的查找
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。
请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
我们一开始的想法很可能是,按顺序遍历数组,如果当前数字比目标数字小,那么目标数字应该在当前数字的右边或者下面,如果比当前数字小,应该在目标的左边或上面,如果我们从第一个值开始,发现比目标数字小,从这里选择右边还是下面便成了一个难题。
这道题目的关键是:从右上角的数字开始比较,因为右上角这个数字,比它大就往下,比它小就往左,这样不会存在分歧的路径,题目就变得简单了
1 | def getNumFromArray(l, num): |
java版:
1 | public boolean Find(int target, int[][] array) { |
字符串
在c++中,字符串是以\0结束的,因此如果复制一个长度为10的字符串,需要初始化一个长度为11的char数组
1 | char str[11]; |
面试题5:替换空格
请实现一个函数,把字符串中的每个空格替换成”%20”。例如输入“We are happy.”,则输出“We%20are%20happy.”。
在网络编程中,如果URL参数中含有特殊字符,如空格、’#’等,可能导致服务器端无法获得正确的参数值。我们需要将这些特殊符号转换成服务器可以识别的字符。转换的规则是在’%’后面跟上ASCII码的两位十六进制的表示。比如空格的ASCII码是32,即十六进制的0x20,因此空格被替换成”%20”。再比如’#’的ASCII码为35,即十六进制的0x23,它在URL中被替换为”%23”。
在python中实现这个问题的方法可以直接调用replace或者是用一个新的字符串,如果当前字符串等于空格,则加%20否则加上当前值,但这样会使用一个O(n)的辅助字符串
1 | def replaceBlank(string): |
java版本:
1 | public String replaceSpace(StringBuffer str) { |
在C++当中解决这个问题的方法是:用两个index,先遍历字符串算出空格的数量,求出字符串长度和更改之后的字符串长度,p1指向原始数据的结束字符,p2指向替换之后数据的结束字符,p1每次往前走一格,p2每次复制p1当前值并同时往前走一格,如果遇到空格则p2加入%20三个字符,而p1往前走一格,直到p1和p2相等或p1为0。
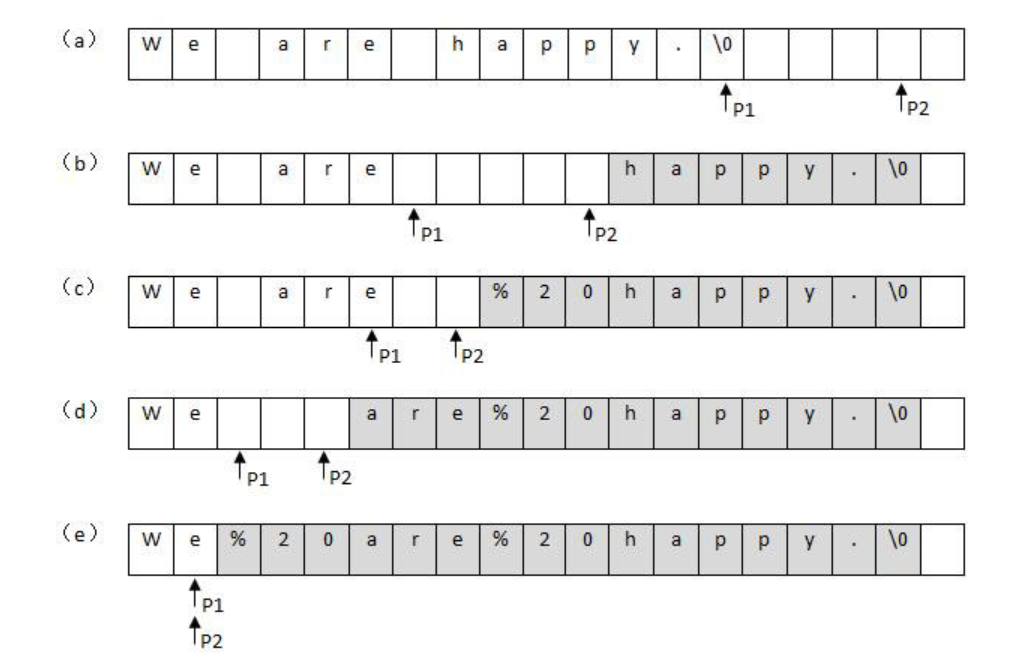
1 | public static void ReplaceBlank(char[] target, int maxLength) |
这道题给我们的启发:如果合并两个字符串或者是数组的时候,从前往后合并往往会需要复制很多次,那么我们可以从后往前合并。
链表
链表是面试中最常出现的数据结构。
链表的空间是用到的时候再分配的,因此空间效率比数组要高。
单向链表的定义如下:
1 | struct ListNode{ |
在链表后面添加一个元素的方法如下:
1 | void addToTail(ListNode** pHead, int value){ |
注意:上面函数的第一个参数,用的是指针的指针,其原因是当pHead为nullptr的时候,要改变pHead的指向,如果传递一个指针的话,只能改变指针指向的对象的值,而不是直接改变他指的地址。
在链表中找到并删除某个元素:
1 | void RemoveNode(ListNode** pHead, int value){ |
面试题6:链表从尾到头打印
输入一个链表的头结点,从尾到头反过来打印出每个节点的值
链表的定义如下
1 | struct ListNode{ |
思路:通常来说,链表只能从前到后访问,如果要从后往前打印,那么我们可以利用堆栈,每遍历一个链表节点,我们将他的值放在栈中,因为栈是后进先出的特性,最后将所有元素出栈,打印即可。
1 | void PrintReverseList(ListNode *pHead){ |
既然用到了堆栈,那么就自然想到了递归,因为递归调用本质就是使用堆栈,递归的链表反转打印方法如下
1 | void PrintReverseList(ListNode *pHead){ |
链表反转
链表反转和上面的思路基本一样,就是递归
1 | ListNode* ReverseList(ListNode* pHead) { |
java版:
1 | public ListNode ReverseList(ListNode head) { |
解释:翻转 [head, n1, n2, n3, …],等于先翻转 [n1, n2, n3, …] ,再把 head 放到最后
head.next 就是 [n1, n2, n3, …],翻转就是 reverseList(head.next),结果是 […, n3, n2, n1],注意 head.next 现在仍然指向 n1,也就是最后
所以,next_node = head.next 等于 next_node 赋值为 n1,也就是末尾的结点
然后 next_node.next = head,就是构造 […, n3, n2, n1, head]
head.next = None,就是把 head 指向 n1 去掉,就翻转了
非递归:
1 | //非递归 |
树
树是实际编程中常用的数据结构。它的逻辑很简单:除根节点外的所有节点都只有一个父节点,根节点没有父节点;除叶子节点外的所有节点都有一个或多个子节点,叶子节点没有子节点。父节点和子节点通过指针连接。
因为树的操作涉及大量的指针操作,因此关于树的面试题难度较大。
面试中提到的树大部分是二叉树。二叉树是一种特殊的树结构,每个节点最多只能有两个子节点。二叉树中最重要的操作就是遍历:
- 前序遍历:先访问根节点,再访问左子节点,最后访问右子节点
- 中序遍历:先访问左子节点,再访问根节点,最后访问右子节点
- 后序遍历,先访问左子节点,再访问右子节点,最后访问根节点
这个前中后都是相对于根节点来说的,前就是先遍历跟节点,中就是根节点在中间,后就是根节点在最后。
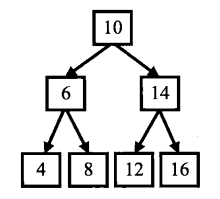
如上的二叉树,我们对其进行上述三种遍历:
- 前序遍历:10,6,4,8,14,12,16
- 中序遍历:4,6,8,10,12,14,16
- 后序遍历:4,8,6,12,16,14,10
这3种遍历,都有递归和循环两种方法,递归实现比循环简洁,要求3种遍历的6种实现方法都要掌握。
二叉树有很多特例,二叉搜索树就是其中之一。二叉搜索树中左子节点总是小于等于根节点,右子节点总是大于等于根节点。这就可以在O(logn)的时间内根据数值找到一颗二叉搜索树的一个节点,
二叉树还有两个特例是,堆和红黑树。
堆分为最大堆和最小堆,最大队中根节点的值最大。最大堆中根节点的值最大,最小堆中根节点的值最小。有很多需要找到最大最小值的问题可以用堆来解决。
红黑树是把树中的节点定义为红黑两种颜色,并通过规则确保从根节点到叶节点的最长路径的长度不超过最短路径的两倍。
面试题7:重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
先理一下这道题的思路,有两个重要信息:①前序遍历的第一个值必然是根节点;②中序遍历中,根节点左边的值必然是左子树,根节点右边的值必然是右子树。那么只要给定一个前序遍历和中序遍历,我们就可以找到他的根节点和左右子树,这样只要递归下去,就能构建出整棵树。
1 |
|
下面是python版本的代码:
1 |
|
java版本:
1 | public static TreeNode reConstructBinaryTree(int[] pre, int[] in) { |
面试题8:二叉树的下一个节点
给定一棵二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
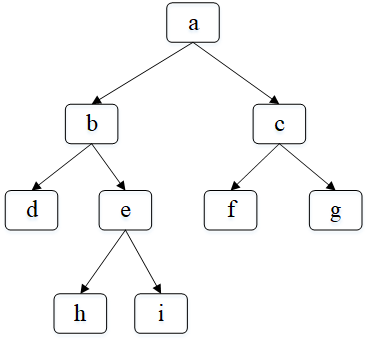
思路:这道题就是一个分情况讨论的方法:
- 如果一个节点有右子树,那么右子树的最左下子树就是下一个节点
如上图:b的下一个节点就是其右子树e的最左子节点h - 如果一个节点没有右子树,但它本身是其父节点的左子树,那么下一个节点就应该是它的父节点
如上图:h的下一个节点是e - 如果一个节点没有右子树,且是父节点的右子节点,那么就一直向上遍历,直到找到一个节点的父节点的左子节点是自己,那么就返回这个父节点,如果遍历到根节点还是空,那么就返回空
如上图:i没有右子树,且不是父节点的左子节点,i的下一个节点就要向上搜索,找到e,e不是b的左子节点,继续向上,找到b,b是a的左子节点,因此返回b的父节点a
下面是python版本的实现
1 | class Solution: |
以下是c++版本
1 | /* |
java版本:
1 | public TreeLinkNode GetNext(TreeLinkNode pNode) { |
栈和队列
栈是一个非常常见的数据结构,在计算机中广泛使用。比如操作系统给每个线程创建一个栈来存储函数调用时各个函数的参数,返回地址及临时变量等。
栈的特点是后进先出,最后被push的元素或第一个被弹出(pop)。
队列的特点是先进先出。
面试题9:用两个栈实现队列
用两个栈实现一个队列,队列的声明如下,请实现他的两个函数appendTail和deleteHead,分别完成在对未插入节点和在队列头部删除节点的功能
1 | template <typename T> class CQueue{ |
思路:两个栈实现一个队列,先把元素全部压入一个栈,在要删除队首元素的时候,将元素全部出栈,然后顺序压入另一个栈,再pop掉最上面一个元素,也就是最先入栈的元素,就删除了头部。加入尾部就直接压入第一个栈就行了。只要第二个栈不为空,我们就从第二个栈中pop,否则将第一个栈全部压入第二个栈。
1 | template <typename T> void CQueue<T>::appendTail(const T& node){ |
1 | template <typename T> void CQueue<T>::deleteHead(){ |
下面是python的实现:
1 | # -*- coding:utf-8 -*- |
java
1 | package com.drawon; |
算法与数据结构
很多算法都可以使用递归和循环两种方法,递归实现比较简洁,但是性能不如基于循环的实现方法。
排序和查找是面试时考察的重点。准备时应该重点掌握二分查找,归并排序,快速排序,做到能随时能正确、完整地写出它们的代码。
如果面试题要求在二维数组上搜搜路径(比如迷宫或者棋盘),我们可以尝试回溯法。回溯法很适合用递归的代码实现。如果面试官规定不允许使用递归,那么就需要用栈来模拟递归。
如果面试题是求某个问题的最优解,并且该问题可以分为多个子问题,那么我们可以使用动态规划。再用自上而下的递归思路去自动分析动态规划问题的时候,我们会发现子问题之间存在重叠的更小的子问题。为了避免不必要的重复计算,我们用自下而上的循环代码来实现,就是把子问题的最优解先算出来并用数组(一般是一维或者二维数组)保存下来,接下来基于子问题的解计算大问题的解。
如果告诉面试官动态规划的思路之后,免死关提醒说分解子问题的时候是不是存在某个特殊的选择,采用特殊选择一定能得到最优解,那么意味着这道题可能可以用贪婪算法。
递归和循环
如果需要重复多次计算相同的问题,则通常可以选择用递归或循环两种算法。递归就是在函数的内部调用这个函数自身。循环是通过设置初值和种植条件,在一个范围内重复运算。
面试题10:斐波那契数列
求斐波那契数列的第n项
斐波那契数列定义如下:
$$
F_0=0\
F_1 =1\
F_{(n)}=F_{(n-1)}+F_{(n-2)}
$$
这是一个使用递归的直观例子,得到的代码如下:
1 | # -*- coding:utf-8 -*- |
但是,在这里使用递归有很大的问题,那就是会进行大量的重复计算,比如我们要得到$f(10)$,首先要计算$f(9)$和$f(8)$,要得到$f(9)$又要得到$f(8)$和$f(7)$,这里,$f(8)$就已经重复了,往后还有很多这样的重复,如图所示
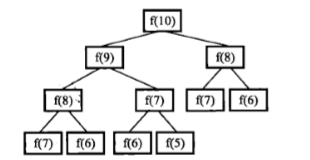
因此,斐波那契数量的正确做法应该是循环,如下所示:
1 | # -*- coding:utf-8 -*- |
青蛙跳台阶
一只青蛙,一次可以跳上一级台阶,也可以跳上两级台阶,那么跳上n级台阶一共有多少种方法。
解析:因为青蛙最后一步,要么跳2级,要么跳1级,那么$f(n)=f(n-1)+f(n-2)$,这样一来,这其实就是一个斐波那契数列问题
程序:python版本
1 | # -*- coding:utf-8 -*- |
c++版本
1 | class Solution { |
变态青蛙跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
解析:我们考虑一下n级台阶的时候有多少种跳法,第一步有n种跳法:跳1级、跳2级、到跳n级。跳1级,剩下n-1级,则剩下跳法是f(n-1);跳2级,剩下n-2级,则剩下跳法是f(n-2),所以$f(n)=f(n-1)+f(n-2)+…+f(1)+1$。同理可以推出$f(n-1)=f(n-2)+f(n-3)+…+f(1)+1$,因此$f(n)=f(n-1)+f(n-1)=2\times f(n-1)=2\times2\times f(n-2)=…=2^{n-1}f(1)=2^{n-1}$
所以,直接返回$2^{n-1}$即可
1 |
|
矩阵覆盖问题
用一个2*1的小矩形,横着或者竖着覆盖一个更大的矩形,请问用8个2*1的小矩形无重复的覆盖一个2*8的大矩形,总共有多少种方法?
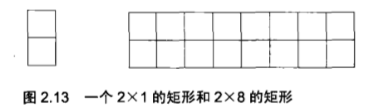
分析:如果我将第一个矩形竖着放,那么就剩下2*7个矩形,如果我将第一个矩形横着放,那么横着放的矩形下面一定是一个横着放的矩形,那么就剩下2*7个矩形,也就是$f(8)=f(7)+f(6)$,可以看出,这依然是一个斐波那契数列问题。
1 | class Solution { |
查找和排序
查找和排序是程序设计中经常用到的算法。查找比较简单,不外乎顺序查找,二分查找,哈希表查找和二叉排序查找。哈希表最主要的有点事能够在O(1)时间内找到某个元素,但是需要额外空间来实现哈希表。二叉排序树查找算法对应的数据结构是二叉搜索树。
排序比较复杂,通常要求比较插入排序,冒泡排序,归并排序,快速排序等不同算法的优劣。要求应试者对各种排序算法烂熟于胸,能够从额外空间小号,平均时间复杂度和最差时间复杂度等方面去分析他们的优劣。很多面试官要求应聘者写出快速排序的代码。
快速排序的关键在于选择数组中选择一个数字,接下来把数组中的数字分为两部分,比选择的数字小的数字移到数组左边,比选择大的数字移到数组右边。实现代码如下
1 | def partion(nums, l, r): |
归并排序如下:
1 | def merge(left, right): |
插入排序如下:
1 | public static void insertionSort(int[] nums) { |
面试题11:旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
思路:想要找到最小的数字,最简单的想法就是直接遍历整个数组,这样就可以找到最小值,但是这样的时间复杂度是O(n),明显没有利用这道题给出的非减数组和旋转数组的概念,这道题正确的解答方式是二分查找,时间复杂度为O(log(n))。
可以使用二分查找的原因是,整个数组可以分成两个非递减的子数组,最小值一定在第二个子数组的第一个元素。
二分查找就是两个指针,一个指向开头,一个指向结束,每次找到中间元素,如果中间元素大于等于开头元素,那么这个元素一定属于前半个子数组,最小值一定在当前中间值和末尾值之间,那么移动第一个指针到当前值的下一个值;如果中间元素小于最后一个值,那么当前元素一定属于第二个子数组,那么最小值一定在开头到当前值之间,移动第二个指针到当前值。
1 | class Solution: |
上面的代码似乎可以成功,但是遗漏了一种特殊情况,如[1,1,0,1,1,1,1],这样,你无法通过比较大小来缩小范围,遇到这样的情况,只能顺序查找。修改代码如下:
1 | class Solution: |
还有一个比较好的办法就是让中间值和右边值比较
- 如果中间值比右边值大,那么证明最小值在中间值右边
- 如果中间值<右边值,r=mid
- 如果中间值等于右边值,r=r-1,有重复值的情况只能一个一个找
1 | # -*- coding:utf-8 -*- |
回溯法
回溯法非常适合有多个步骤组成的问题,并且每个步骤有多个选项。用回溯法解决的问题,可以形象的用树表示,每一步都有m个可能选项。如果叶节点的状态满足题目约束条件,则找到了可行方案。
面试题12:矩阵的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则之后不能再次进入这个格子。 例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串”bcced”的路径,但是矩阵中不包含”abcb”路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
1 | # -*- coding:utf-8 -*- |
面试题13:机器人的运动范围
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
思路:这道题有一个小陷阱,这个机器人只能一步一步地走,如果使用循环,遍历所有节点是否满足加和的条件,在比如rows=1或者cols=1的时候,节点不能跨越其他节点访问,就会出错。因此使用的是回溯法,给定一个visited矩阵,如果节点在范围内且没有被访问过,且满足阈值条件,检查他和他的下一个节点是否满足条件,依次回溯。
1 | # -*- coding:utf-8 -*- |
动态规划和贪婪算法
动态规划是编程面试的热门。如果面试题是一个问题的最优解(通常是求最大值或者最小值),而该问题可以分解成若干个子问题,并且子问题之间海鸥重叠的更小的子问题,就可以考虑用动态规划来解决这个问题。
在用动态规划之前应该分析能否把大问题分解为小问题,且分解后的每个小问题也存在最优解。
贪婪算法是在每一步都进行一个贪婪选择,具体可以看下面这个例子,用了贪婪算法和动态规划两种方法解决。
面试题14:剪绳子
给你一根长度为n的绳子,请把绳子剪成m段 (m和n都是整数,n>1并且m>1)每段绳子的长度记为k[0],k[1],…,k[m].请问k[0]*k[1]*…*k[m]可能的最大乘积是多少?例如,当绳子的长度为8时,我们把它剪成长度分别为2,3,3的三段,此时得到的最大乘积是18.
方法1:动态规划
思路:动态规划首先要定义一个长度为n或者是n+1的数组,用于存放每个子问题的最大或最小值,这道题里面我们定义了一个maxv数组,长度为n+1,给定数组的前几个值,直到可以用子问题解决的时候,开始使用循环,第一个循环是长度为n的,第二个循环是每次剪长度为1,长度为2,长度为n-1的情况,这样第二个循环有重复,因为一刀剪1和一刀剪n-1是重复的,因此,每次只需要重复i/2即可。
1 | def cutLine(length): |
方法2:贪婪算法
思路:尽可能剪长度为3的绳子,直到长度小于等于4,等于四的时候,剪成2*2的乘积比1*3要大,所以为4的时候剪成2*2。这个可以通过数学方法证明,当n>=5的时候,3(n-3)>=2(n-2)的,当n=4的时候,有两种切法,一种是
1 | def cutLine(length): |
位运算
位运算主要有五种:与,或,非,异或,移位运算
前面三种比较常见,异或的符号是^,移位运算的符号是<<或者>>。
左移n位,直接丢弃最前面的n位,是负数就在最符号位补1,正数就在符号位补0。右移n位同理。
面试题15:二进制中1的个数
任意给定一个32位无符号整数n,求n的二进制表示中1的个数,比如n = 5(0101)时,返回2,n = 15(1111)时,返回4
思路:第一种思路是一直把给定值右移运算,然后和1做与运算,这样就能判断当前位是否为1,但是这种方法有陷入死循环的可能
第二种思路是将1一直左移,这样每次与的结果都是当前位与1的结果,判断当前位是否为1。
第三种思路是一种很巧妙的方法,先把给定值减去1,如果这个数不等于0,那么该数的二进制表示中至少有一位是1,假设这个数的最右边一位是1,那么减去1之后,最后一位变成0,而其它位保持不变,也就是想防御最后一位相当于做了取反操作,从1变成了0;而如果最后一位不是1,而是0,我们用第m位表示最右边的1所在的位置,减去1之后,m位右边的值取反,m位左边的值不变,举个例子,1100,减去1之后,最右边的1在第二位,第二位之后的所有值取反,第二位左边的值不变,结果是1011。
总结第三种方法提到的特例,发现把1个整数减去1,就是把最右边的1变成0,如果他的右边还有0,则所有0都变成1,而它左边的所有位都不变。那么我们将一个数和它减去1的结果做与运算,相当于把最右边的1变成0,其余所有位都保持不变。那么我们反复这样操作,每进行一次,就少一个1,这样就统计出来有多少个1了。
1 | # 方法1: |
相关题目:
- 判断一个数是否是2的整数次方。
解答:一个数如果是2的整数次方,那么其中一定只有一个1,只需要将这个值和它减1的结果相与,判断1的个数,即可。 - 判断m需要多少步变化才能变成n,比如13的二进制是1101,10的二进制是1010,要把13变成10,需要改变其中的3位。
解答:直接两个值做异或,然后统计其中1的个数即可。
第三章:高质量的代码
面试题16:数值的整数次方
实现函数double Power(double case, int exponent),求base的exponent次方,不得使用库函数,且不需要考虑大数问题。
直观思路是,从1到exponent,result每次乘以base,最后就得到了base次方
1 | double Power(double base, int exponent){ |
这样看上去似乎是对的,但是没有考虑输入指数小于1(零和负数)的情况。接下来在代码中加入对特殊情况的判断。
1 | double Power(double base, int exponent){ |
这样一来,看上去似乎已经完美了,但是还存在更加高效的方法。
假如需要求base的32次方,那么可以先做16次方,然后平方,再继续深究,先做8次方,再平方,再做4次方,平方,再做2次方。也就是只需要做5次乘法即可。这样就大大减少了运算量。
$$
f(x)=\left{
\begin{aligned}
a^n = & a^{n/2}*a^{n/2}\quad a为偶数\
a^n = & a^{(n-1)/2}*a^{(n-1)/2}*a\quad a为奇数
\end{aligned}
\right.
$$
利用上面的公式,就可以通过递归实现整数次方的问题。
1 | double PowerWithUnsignedExponent(double base, unsigned int exponent){ |
java非递归代码:
1 | public static double pow(int base, int exponent) { |
矩阵快速幂
当遇到f(n)=a*f(n-1)+b*f(b-2)的情况,如果用递推公式计算量非常大,因此比较好的方式是用矩阵快速幂,构造如下矩阵乘法:
$$
\left(\begin{array}{cc}{a} & {b} \ {1} & {0}\end{array}\right)\left(\begin{array}{c}{f(n-1)} \ {f(n-2)}\end{array}\right)=\left(\begin{array}{c}{f(n)} \ {f(n-1)}\end{array}\right)
$$
则求f(n)的过程变为:
$$
\left(\begin{array}{cc}{a} & {b} \ {1} & {0}\end{array}\right)^{n-2}\left(\begin{array}{c}{f(2)} \ {f(1)}\end{array}\right)=\left(\begin{array}{c}{f(n)} \ {f(n-1)}\end{array}\right)
$$
此时就可以利用快速幂了,只是把res和base的乘法换成了矩阵乘法
1 | public static double[][] matrixPow(double[][] nums, int exponent) { |
面试题17:打印从1到最大的n位数
题目:输入数字n,按顺序打印出从1到最大的n位十进制数,比如输入3,则打印出1,2,3直到最大的三位数999
陷阱:这道题看起来很简单,直接打印1到$10^n$就行了,但是用int类型会溢出的时候,甚至用 long long 都会溢出的时候怎么办呢?
思路:这道题的正确思路是用字符串来表示数字,因为最大数字是n位的,在c++中,需要给定一个n+1位的字符串,因为结束位是\0,当数字不够n位的时候,在字符串的前半部分补0。首先把字符串中的所有数字都初始化为0,每次喂字符串表示的数字加1,然后打印出来。因此有两个任务,一个是在字符串表示的数字上模拟加法,二是将他们打印出来。
1 | void PrintToMaxOfDigits(int n){ |
模拟加法,每次加1就是从最后一位开始,每次加1,有进位则保留下来继续加下一位,否则结束加法,剩下的位数保持不变。那么什么时候应该继续加,什么时候应该结束加法呢?如果每加1次就和最大值999…999进行比较,时间复杂度每次都是o(n)。其实只需要判断最高位是否有进1,如果有则达到了最大值。
1 | bool Increment(char* number){ |
打印数字也存在小陷阱,如果使用printf直接打印,那么前面那些0也被打出来了,因此应该判断一下,打印第一个不为0的值到最后一个值。
1 | void PrintNumber(char* number){ |
将问题转换为数字排列,递归实现
模拟字符串加法比较复杂,因此可以使用递归进行每一位0-9的排列组合。打印的时候,前面的0不打印即可,递归结束条件是已经设置了数字的最后一位。
1 | void PrintToMaxOfNDigits(int n){ |
面试题18:删除链表节点
在O(1)时间内删除链表节点
给定单链表的头指针以及任何一个节点指针,定义一个在O(1)时间内删除该节点的函数。
思路:这道题最直观的想法就是从头到尾遍历,直到找到这个节点的上一个节点,将该节点的上一个节点的next,指向该节点的next,但是这样的时间复杂度是O(n),不符合要求。
既然时间复杂度是O(1),那么我们当然只能直接利用给定节点,直接给定节点只有两个信息,一个是当前值,一个是next,那么我们可以将next的value复制到当前节点,将当前的next指向next的next,也就成功删除了这个节点。
考虑一下特殊情况,如果当前节点没有下一个节点,也就是当前值本身就是尾节点,那就得从头开始遍历到当前节点,然后将尾节点的前一个节点设置为空。还有一种特殊情况就是当前链表就只有一个元素,直接将头节点置为空就行了,
1 | struct ListNode{ |
通过上面的方法,如果不是尾节点,时间复杂度为O(1),如果是尾节点,时间复杂度为O(n)。平均时间复杂度为((n-1)*O(1)+1*O(n))/n,还是O(1)。
这道题使用上面这种方法,暗含的假设就是待删除节点一定包含在链表中,如果不一定存在,那么这个就只能遍历链表。
题目2
删除链表中重复节点,如果当前值和前一个节点的值相同,那么删除当前节点和前一个节点。
思路:要判断当前节点与后面节点是否重复并删除,要找到当前节点的前一个节点pPreNode,和当前节点的下一个节点pNext,把上一个不重复的节点的next指向下一个不重复的节点即可。
一共定义3个节点,pPreNode,pNode,pNext,用于保存上一个不重复节点,当前节点,下一个节点。
当重复的包含头结点的时候,需要判断,然后将头结点指向第一个不重复的节点。
1 | void deleteDuplicate(listNode** pHead){ |
java版本:
1 | public ListNode deleteDuplication(ListNode pHead) { |
面试题19:正则表达式匹配
请实现一个函数用来匹配包括’.’和’*‘的正则表达式。模式中的字符’.’表示任意一个字符,而’*‘表示它前面的字符可以出现任意次(包含0次)。 在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串”aaa”与模式”a.a”和”ab*ac*a”匹配,但是与”aa.a”和”ab*a”均不匹配
思路:这道题的关键点在于“*”这个字符,如果一个字符的下一个字符不是“*”,直接拿出来跟string里面的字符比较就行。
如果后一个字符是”*“,那么这个问题变得稍微复杂一点。如果后一个是“*”且当前字符与字符串的相符,那么有如下三种情况:
- pattern可以直接跳过2字符,s不变。相当于虽然匹配,但是忽略这个带“*”的内容
- s+1,pattern+2,相当于只匹配当前这一个值
- s+1,pattern不变,相当于当前匹配,接着匹配后面的值
因为只要其中一个符合就为true,因此返回的是上述三张情况的或。
如果当前pattern的下一个字符是“*”,且与当前值不匹配,可以直接跳过pattern的2个字符,忽略这个”*“部分
1 | # -*- coding:utf-8 -*- |
这道题用的方法也是递归
java版本:
1 | public static boolean match(char[] str, char[] pattern) { |
面试题20:表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串”+100”,”5e2”,”-123”,”3.1416”和”-1E-16”都表示数值。 但是”12e”,”1a3.14”,”1.2.3”,”+-5”和”12e+4.3”都不是。
比较直观的思路就是直接一堆条件判断,比如第一位0-9或者是+-号,出现e之后不能出现”.”,每个字符只能是0-9或者是”+-eE.”,写这道题的思路比较乱,这样容易漏掉情况
1 | # -*- coding:utf-8 -*- |
书中给的方法十分有逻辑,首先用scanInterger扫描第一位是不是+或-,如果是,继续扫描后面是不是数字,如果出现小数点,则扫描小数点部分,如果出现e,则扫描指数部分
1 | bool match(const char* str){ |
java版本:
1 | public static boolean checkNum(char[] num) { |
面试题21:调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
如果用python这道题很简单,遍历数组,是奇数就放到一个list中,是偶数放到另一个中,最后做一个extend。
1 | # -*- coding:utf-8 -*- |
用c++会复杂一下,维护两个指针,一个指向数组开头(*begin),一个指向结尾(*end),只要begin<end,begin向后移动到第一个偶数,end向前移动到第一个奇数,两者交换。
代码鲁棒性
面试题22:链表中倒数第k个节点
输入一个链表,输出该链表中倒数第k个结点。
这道题的思路就是维护两个指针,第一个指针先向前走k-1步,第二个指针开始开始和第一个指针一起向后走,直到第一个指针指向最后一个元素,此时,第二个指针刚好指向第k个元素。
这道题考察的主要要点是鲁棒性:
- 如果链表长度小于k怎么办
- 如果输入的是空链表怎么办
- 如果输入的k是0怎么办(因为这道题说的最后一个节点是倒数第1个节点)
1 | # -*- coding:utf-8 -*- |
java版本:
1 | public static ListNode reverseKthNode(ListNode head, int k) { |
面试题23:链表中环的入口节点
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
这道题可以用暴力方法解决,遍历链表,每遍历一个节点,就将其放入一个list中,直到再次在list中找到这个节点,那么返回节点,如果一直没有找到,返回None
1 | # -*- coding:utf-8 -*- |
书中给出的方法是充分利用了c++的指针,给定两个指针,一个每次移动2格,一个每次移动1格,那么每次移动两格的一定会追上每次移动一格的,两者相遇的时候,就表明链表中有环。
从这个相遇节点出发,再次回到这个相遇节点,每走一步加1,就统计出了环中元素的个数n。那么再给两个指针指向链表头部,其中一个先移动n格,然后两个一起移动,每次一格,相遇的点即为环的入口。
1 | public static ListNode enterNodeOfCircle(ListNode head) { |
面试题24:链表反转
讲一个给定的单向链表进行反转
1 | # -*- coding:utf-8 -*- |
面试题25:合并排序链表
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
1 | # -*- coding:utf-8 -*- |
面试题26:树的子结构
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
基本遇到树的问题,思路都是递归,这道题一共两个递归,第一个递归遍历第一棵树,如果找到某个节点和tree2的根节点相同的,开始第二个递归,第二个递归检查tree1的左右子树的值是不是跟tree2一样,直到遍历完tree2,此时返回True,其余情况均返回false(tree1为空或者某个地方值不等)
1 | class Solution: |
还有一种写法比较简洁,思路是如果一来其中一个为空,就返回false,否则进入一个递归,分别是从当前节点判断是否包含,从左子树判断是否包含,从右子树判断是否包含。判断方法与上述的第二个函数相同。
1 | class Solution: |
java版本:
1 | public static boolean subTree(TreeNode root1, TreeNode root2){ |
在python中是直接用==判断值是否相等的,而如果是c++,值如果定义为double类型,判断方法是两者相减是否>-0.000000001 & <0.000000001
做这道题的时候,顺便看了树的遍历方法,思路就是如果树为空,返回,如果不为空,先打印值,然后遍历左子树,然后遍历右子树,这下面的是树的前序遍历,中序遍历和后序遍历只是把print的位置换一下,如下:
1 | #递归前序遍历 |
还有层序遍历,层序遍历的思路是维护一个list,每次把当前节点的左右子节点都压入list,只要这个list不为空,就一直pop最先进入list的元素出来打印
1 | def layer(tree) |
第四章:解决面试题的思路
在面试中,当面试官说出题目之后,不应该立即动笔开始写代码,而是应该先理清思路,给面试官讲一遍完整的思路,再开始写。举例子和画图都是比较好的解释思路的方法。
画图让抽象问题形象化
有些面试题可能比较抽象,可以尝试多画几张图,找几个例子画出来,说不定就能看出规律,从而解决问题。
面试题27:二叉树的镜像
操作给定的二叉树,将其变换为源二叉树的镜像。
可以一开始不理解什么是镜像,画几张图就可以明白
1 | 二叉树的镜像定义:源二叉树 |
这个题目和遍历很像,这是把遍历的print换成了左右子节点换顺序
1 | class Solution: |
面试题28:对称的二叉树
请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
思路:如果定义一棵树的先序遍历有两种:一种先访问左子节点,一种先访问右子节点,只要这两种遍历方式相同,那么这棵树就是对称二叉树。具体而言:左子树的左子节点变成了右子树的右子节点,左子树的右子节点,变成了右子树的左子节点,只要这个变化之后的值始终相同,那么这棵树就是对称的。
1 | class Solution: |
面试题29:顺序打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
这道题我一开始的思路是直接暴力解决:先一直向右,直到最右端;然后一直向下,直到最下端;然后向左,直到最左边;然后向上,到最上面。判断结束的条件是每一个节点都被访问过了,最后要求返回的值是一个包含所有元素的数组。
1 | class Solution: |
暴力方法虽然可以解决这个问题,但并不是一个好选择。
这道题的关键之处在于:顺时针打印就相当于按圈打印矩阵,每一个圈的起始点都是顺序主子矩阵的最左上方的节点

那么打印到什么时候结束呢,当矩阵是4*4的时候,最后一个开始节点是(1,1),当矩阵是5*5的时候,最后一个开始节点是(2,2);当矩阵是5*4的时候,结束点还是(1,1)。从这几个可以总结出规律,结束条件是cols>=start*2,或者rows>=start*2
每一圈还有个结束条件,$endx=cols-1-start,endy = rows-1-start$
写出代码如下:
1 | class Solution: |
举例让抽象问题具体化
通过举例模拟的方法来分析复杂的问题。当一眼看不出问题隐藏的规律的时候,试着用一两个具体的例子模拟操作的过程,说不定能通过具体的例子找到抽象的规律。具体例子还有助于保证代码质量。测试用例可以用来测试结果是否与预期一致。
面试题30:包含min函数的栈
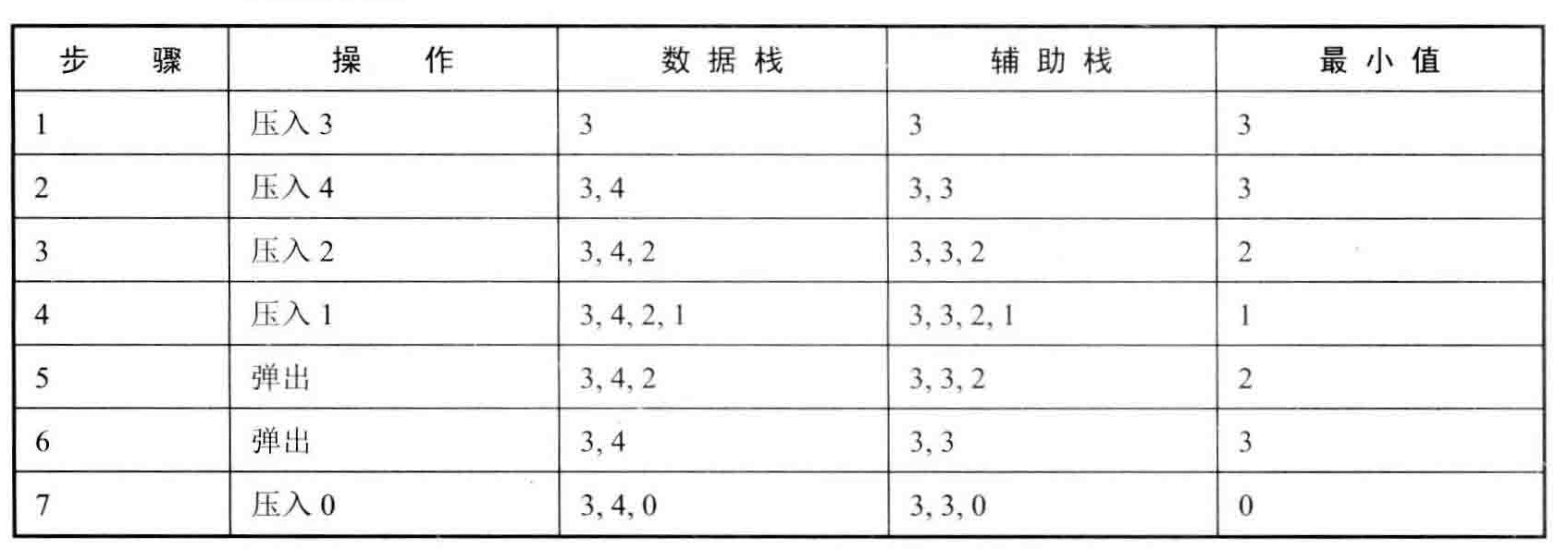
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
思路:一看到这道题,很可能的想法,就是直接实现一个栈,然后把栈元素的最小值保留下来,但是这种方法存在一个问题,就是如果当前pop出来的元素就是最小值,然后再求最小值就不存在了;自然而然想到把倒数第二小的元素也保存下来,那倒数第二小的元素也被pop出来了怎么办呢?这样的思路考虑下去,那就是把所有最小值都保存下来。
我们举个例子来模拟一下这个步骤,每次压入一个元素到stack中,同时将当前最小值压入min_stack中,每次从stack pop元素的时候,同时从min_stack pop一个元素,这样能够保证min_stack最上面的值就是当前栈的最小值。
这道题的关键就在于需要一个辅助栈,用于存放每一步的最小值。
1 | # -*- coding:utf-8 -*- |
面试题31:栈的压入,弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
思路:给定push的顺序和pop的顺序。遍历pop顺序,如果当前要pop的元素不在栈中,将按照push顺序一直入栈到当前需要pop的元素,然后pop掉最后一个入栈的元素。遍历完整个pop序列,如果stack为空,则存在该pop序列,否则不存在。
1 | # -*- coding:utf-8 -*- |
1 | public static boolean pushPopOrder(int[] push, int[] pop){ |
面试题32:从上打下打印二叉树
从上往下打印出二叉树的每个节点,同层节点从左至右打印。
思路:这道题就是一个广度优先遍历问题,给定一个队列,先将根节点入队,只要队列不为空,pop出队列的第0个元素作为当前节点。如果当前节点的左右子节点不为空,就append到队列后面。直到queue为空,结束
1 | # -*- coding:utf-8 -*- |
题目2:
分行从上到下打印二叉树
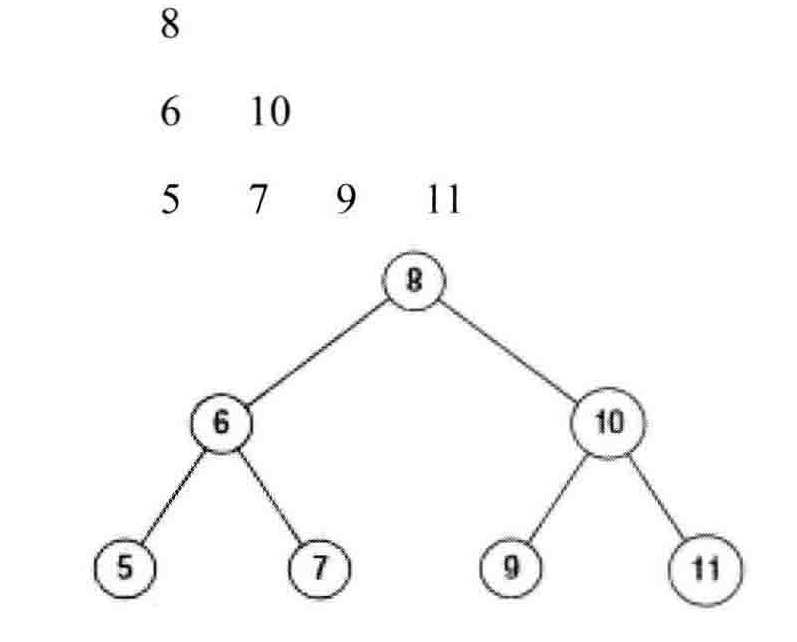
要求同一层的节点打印在一行里面,我一开始想法是每当打印到$2^n-1$的时候,就打印换行符。要判断是不是到了$2^n-1$,只需要将这个值+1,然后与上(n-1),如果这个值的二进制表示中只有一个1,那么就是$2^n$。
上面的方法可以解决问题,但是比较复杂,毕竟要判断$2^n$
书中给的方法是给两个index,一个待打印的数目,一个下一层要打印的数目。
1 | class Solution: |
题目3:
之字形打印一棵二叉树
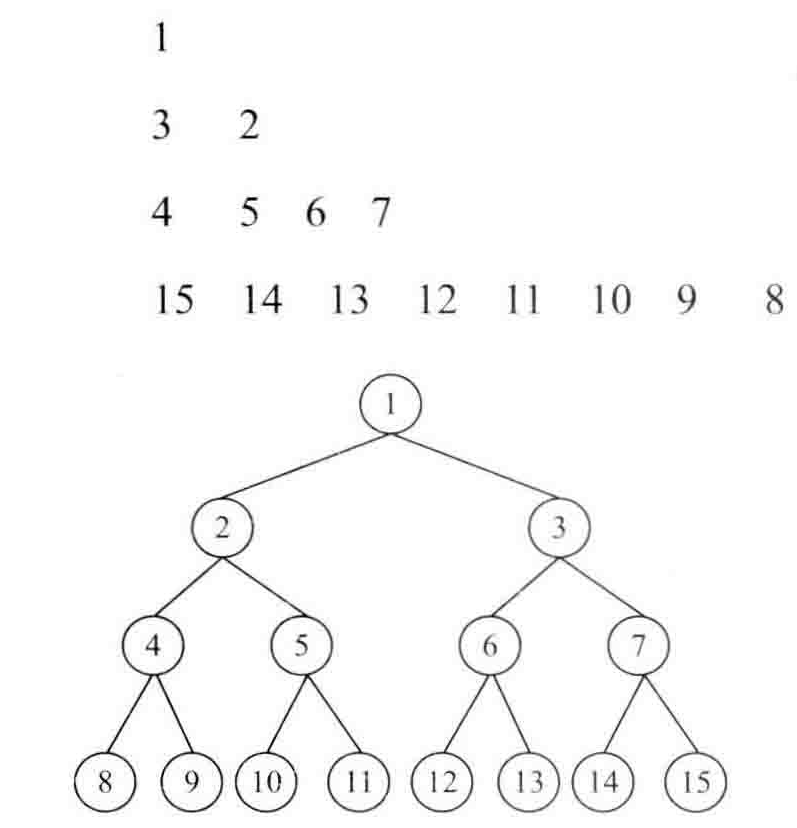
假设根节点处于第1行,奇数行从左到右打印,偶数行从右到左打印。一开始的错误想法是,在奇数行pop(0),偶数行pop最后一个,这样按照上面的例子,先打印1,然后打印3,然后打印7,这就乱了。
正确做法是使用2个栈,为什么使用2个栈,就是因为如果使用一个栈,跟上面错误思路的情况一样,那么打印3的时候,7就入栈了,下一个出栈的是7。两个栈,奇数行先添加右节点,再添加左节点,偶数行正常添加。
1 | class Solution: |
或者改进一下,减少flag的数量,只用一个layer变量,每次用1-layer
1 | class Solution: |
面试题33:二叉排序树的后序遍历
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出True,否则输出False。假设输入的数组的任意两个数字都互不相同。
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
简单来说就是,根节点的左子树的所有节点都比根节点小,右子树的所有节点都比根节点大,且没有重复节点。
要判断一个序列是不是二叉排序树,那就要找出左右子树,然后判断左右子树是不是满足上面的要求,并判断左右子树是不是二叉排序树。
二叉排序树的最后一个节点一定是根节点,第一个比根节点大的值是左右子树的分界线。
先排除意外情况,如果输入为空,返回False;否则进入递归函数。
递归函数是首先从左到右找到第一个比根节点大的值,然后向右一直搜索到最后一个元素,如果中间出现任何一个元素小于根节点,那么就证明不是二叉排序树,返回False。如果一直到最后一个都满足条件,那么就判断左右子树是不是二叉排序树,最后返回left和right子树的and结果。
1 | class Solution: |
java版本
1 | private static boolean isPostVisitCore(int[] nums,int start,int end) { |
面试题34:二叉树中和为某一值的路径
输入一颗二叉树的根节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
思路:先判断给定的是不是空,如果是空,直接返回空list。否则累积加和,如果加和等于值,就把刚才记录的所有值都放入result list中,如果没到叶节点,那么继续向下。递归实现。
1 | # -*- coding:utf-8 -*- |
java版本:
1 | public static ArrayList<ArrayList<Integer>> sumPath(TreeNode root, int target) { |
分解让复杂问题简单化
面试题35:复杂链表的复制
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的head。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)
思路:这道题主要思路,如果从直观来讲,我们先复制所有节点的值以及他们的next关系,第二步去复制random关系,在找random关系的时候,就要从头到尾一个一个找到random节点,如果在原始链表上走s步找到了这个random节点,那么只需要在新链表上同样走s步找到这个新节点。对于长度为n的链表,每次找到random节点都需要O(n)的时间复杂度,因此这种方法总时间复杂度为$O(n^2)$。
1 | #-*- coding:utf-8 -*- |
由于这种方法最主要的时间损耗在于寻找random节点,尝试对该方法进行优化,第一步仍然是复制节点和next关系,但是区别是将这些复制的节点插入到原始链表中,第二步仍然是复制随机节点,这个时候新链表的值就是pCur.next,他的random就指向原始节点pCur的随机节点的复制值,也就是pCur.random.next,就是这个地方大大提升了效率。最后一步是拆分成2个独立的链表。
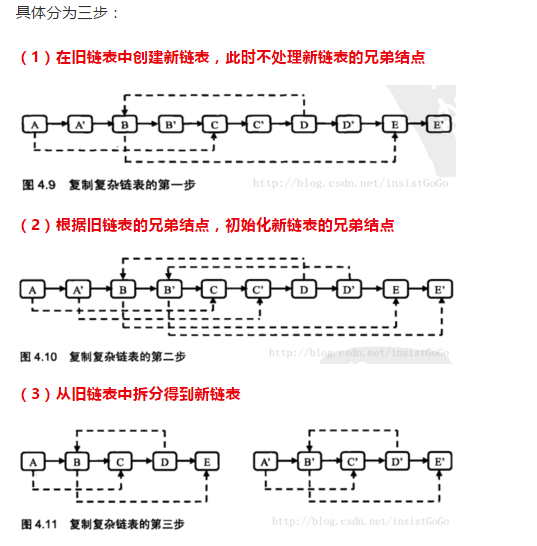
1 | # -*- coding:utf-8 -*- |
java版本:
1 | static class RandomListNode { |
面试题36:二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向
思路:一颗二叉搜索树本身就是排序好的,左子树节点一定小于根节点,右子树节点一定大于根节点,既然要排序,类似于中序遍历的方法,在找到左子树的最大节点时,将左子树的最大节点与根节点双向连接起来;将右子树的最小节点与左子树连接起来。
1 | # -*- coding:utf-8 -*- |
面试题37:序列化二叉树
请实现两个函数,分别用来序列化和反序列化二叉树
1 | # -*- coding:utf-8 -*- |
java版本:
1 | public static String serialize(TreeNode root) { |
面试题38:字符串的排列
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
python有比较取巧的办法,itertools里面有purmutations这个函数,直接列出所有可能的排列组合,然后用’’.join连接起来并去重就得到了结果。
1 | # -*- coding:utf-8 -*- |
如果用正常的思路,应该是通过交换得到,从第一位开始,与后面每一位交换得到组合结果
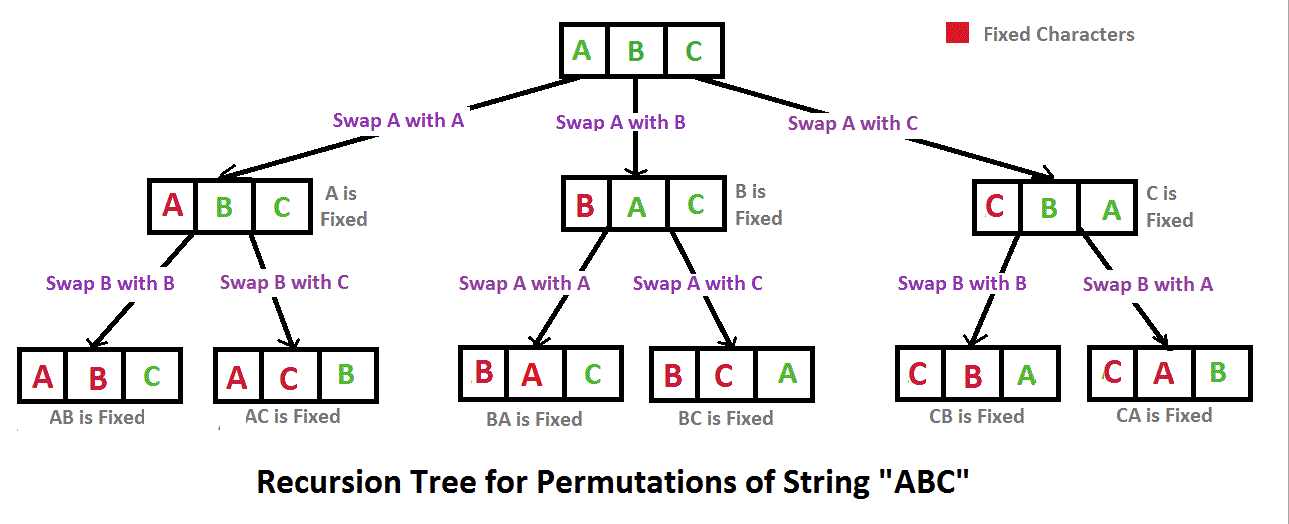
1 | class Solution: |
总结:
求排列的方法:传入一个字符串切割好的list,固定第i位,交换i(自己与自己交换保持位置)及后面的位数,直到已经换到了最后一位了,把结果放入result中。
求组合的方法:传入一个由字符串切割得到的list,要得到长度为m的组合(m可能为0-n,其中n为字符串的总长度),此时可以分为2种情况:选择list的第一位,然后在list的剩下内容中选择m-1位;不选第一位,在list的剩下内容中选择m位,当需要选择的位数为0的时候,证明长度已经达到了需要的长度,此时直接join出结果并存入result中即可。
1 | def getCombine(s): |
第五章:时间效率
面试题39:数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
方法一:字典计数
这种方法直接遍历一遍数组,但是需要辅助的字典来存储每个数字出现的次数,时间复杂度为o(n),空间复杂度为o(n)
1 | # -*- coding:utf-8 -*- |
方法二:基于快排的partion函数
因为要找的是出现次数超过一半的数,那么这个数一定是横跨length/2的,因为只要超过一半,中位数那个值一定是需要找的值,那么我们只需要找到中位数就行了。利用partion函数,每次找一个值,直到找到中位数的值。
partion函数是随机选一个数,把所有小于选中值的放在其左边,大于选中值的放在其右边,如果此时选中值的index小于length/2,那么证明中位数在其右边,反之证明中位数在其左边,循环换值,直到找到中位数。
1 | # 方法2:基于partion函数 |
方法三:基于数组特点进行查找
一个数字如果出现次数超过数组长度的一半,那么这个数字出现的次数就比其它所有数字出现次数的和还要多
我们利用两个变量:numNow和countNow来表示当前指定的数和其出现的次数。
- 如果countNow大于0,出现一个和numNow相同的值,那么countNow+1,;出现一个和numNow不同的值,countNow减1。
- 如果countNow小于等于0,那么就需要更换当前的数字
1 | class Solution: |
面试题40:数组中最小的k个值
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
方法一:利用partion函数进行排序*,时间复杂度为O(n)
在可以改变数组的情况下,用partion进行排序,找到第k大的值,partion是将比选定值小的放在左边,比选定值大的放在右边,那么k之前的就是最小的k个值
1 | # -*- coding:utf-8 -*- |
方法二:时间复杂度为O(nlogk)的方法,基于红黑树
面试题41:数据流中的中位数
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中位数。
这道题的方法是使用两个堆,一个最大堆,一个最小堆,同时保证最小堆的最小值比最大堆的最大值更大,在当前元素个数为偶数的时候,新来的元素加入最小堆,当前元素个数为奇数的时候,新来的元素加入最大堆。
面试题42:连续子数组的最大和
输入一个整形数组,数组里有正数有负数。数组的一个或连续多个数组组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)
这道题最直观的思路,就是枚举所有子数组并求和,子数组的总数是n*(n-1)/2(长度为1的子数组有n个,长度为2的子数组有n-1个…长度为n的子数组有1个,所以总个数是n+n-1+n-2+…+1),这样时间复杂度至少为$O(n^2)$。
正确的做法是使用动态规划,累计加和数组中的元素,如果当前累积和大于0,那么下一次加和的时候继续加上这个累计和,如果当前结果已经小于0了,呢么下一次加和的时候就舍弃前面的累积和,重新加和。这样得到的结果就是加到当前位置的最大累计和。也就是子数组的最大和。
1 | # -*- coding:utf-8 -*- |
面试题43:1~n中数字1出现的次数
求出1
13的整数中1出现的次数,并算出1001300的整数中1出现的次数?为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数(从1 到 n 中1出现的次数)。
最直观的方法肯定是通过循环,对每个数有多少个1进行判断,代码如下:
1 | # -*- coding:utf-8 -*- |
这种方法的时间复杂度太高了,因此需要进行优化。
剑指offer上面给出的优化方法是:给定一个数,例如21345,我们先看他是五位数的时候,有多少个1,再看他4位数有多少个1,再看2位数有多少个1,直到为1位数,递归求得总共1的数目。
在判断每次有多少个1的时候,又可以分为这样的方法:21345,万位为1的有10000个;剩下4位,其中某一位为1的时候,另外3位都可以在0-9之间变化,就是$10^3$种组合,而万位可以在1,2之间变化,总组合数就是$2\times10^3\times4$,到这里,五位数的情况就分析完了,下面分析4位数的情况。四位数只有1345,分析千位是1的情况,有345个,剩余方法类似。
这种方法可理解性并不好,在牛客上面看到一种更容易被理解的方法。
给定一个数字,比如还是21345,个位出现1的次数是(2134+1)*1次,十位出现1的次数是(213+1)*10次,百位出现1的次数是(21+1)*100次,千位出现1的次数是2*1000+346次,万位出现的次数是10000次。
出现次数的规律是这样的:
- 比如我们要找个位出现1的次数,先把数据分成2部分:2134和5,5之前的值可能是0-2134一共是2135次;
- 找十位的时候,分成两部分:213和45,0-213共214种组合,每种组合出现1的次数是10(十位为1,个位0-9之间变化),也就是214*10次;
- 百位的时候分成:21和345,一共是100*22种;
- 千位的时候分为2和1345,这个时候情况就和前面不一样的,因为这次末尾的最高位是1,当第一部分在0-1之间变化时,情况不变得到2*1000种,但是当第一位为2的时候,只有345+1=346种,那次是一共是2346种;
- 万位的时候分为没有和21345,此时是1*10000种一共
可以看出,只要当前要找的那一位大于等于2,那么就可以直接是前面的部分+1乘以当前的10的次方,如果当前那一位等于1,就要找当前位的后面几位+1加上前面的结果,如果当前位为0,那就只有前面部分。
下面代码中用(a+8)//10的原因就是用于判断当前位是不是大于等于2
1 | public class S43r { |
面试题44:序列中某一位的数字
数字以1234567891011121314…这样的规则排列,在这个序列中,第5位是5,第13位是1,第19位是4,写出一个函数,可以求得第n位对应的数字
这道题的思路就是,1-9之间有9个数字,10-99之间有90个数字,100-999之间有900个数字,分别占据9位,90*2=180位,900*3=2700位,如果我现在找1001位,那么肯定不在9位这部分里,跳过 ,剩下992位,也不再10-99之间,跳过,剩下992-180=812位,812是小于2700的,所以肯定在这个范围内,这个范围的起始值是100,(812-1)//3=270,那么就是从100开始的第270个值,也就是370,(812-1)%3=1,也就是中间那一位7
1 | class Solution: |
面试题45:组合出最小数字
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
思路:这道题主要是进行一个自定义的比较函数,如果a+b比b+a字符串连接的结果小,那么两者交换。这个比较函数定义在compare中,比较算法就是普通的冒泡排序即可。
P.S.冒泡排序助记:i[0,n)->j[0,n-1-i)
1 | class Solution: |
面试题46:把数字翻译为字符串
给定一个数字,按照如下规则翻译成字符串,0翻译成”a”,1翻译成”b“,11翻译成”l“,…,25翻译成”z“,一个数字可能有多种翻译,例如12258有五种翻译,请实现一个函数,能够计算一个数字有多少种翻译。
这道题的关键在于写出递推关系式:$f(i) = f(i+1) + g(i,i+1)\times(i+2)$,f(i)表示从第i个数字开始,有多少种不同的翻译方式。
这显然是一个递推的公式,如果用递推的写法来解决这个问题,效率比较低,因为有很多重复的情况,比如f(0)=f(1)+g(0,1)*f(2),f(1)=f(2)+g(1,2)*f(3),f(2)=f(3)+g(1,2)*f(4),这里就已经重复了f(2),f(3)的计算过程。
递归是通过最终问题自上而下(从未知开始,在已知的时候退出)的解决,那如果通过循环自下而上(从已知开始,最终找到未知)的解决问题,就效率比较高了。
1 | # 方法1:递归 |
面试题47:礼物的最大价值
在一个m×n的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格,直到到达棋盘的右下角。给定一个棋盘及其上面的礼物,请计算你最多能够拿到多少价值的礼物。
这道题也是动态规划,要写出递推公式就比较好做
用f(i,j)表示到(i,j)这个坐标时,能去得到最大礼物值,那么$f(i,j) = {\rm gift}[i][j]+\max(f(i-1,j),f(i,j-1))$,可以用递归的方法实现,但是效率低,最终依然用循环来实现
1 | class Bonus: |
优化空间复杂度为O(n):只有一维数组来存储最大值,数组每一个值maxVal[j]表示的是第i行,到第j列为止的最大礼物值,因此maxVal[j-1]表示左侧的最大值,而maxVal[j]在更新之前表示的就是上一行的最大值it
1 | public static int maxValueOptimize(int[][] gifts) { |
面试题48:最大无重复子串
请从给定字符串中找到一个最长的不包含重复字符串的子字符串,计算该字符串的长度
书中给的方法是动态规划,用f(i)表示到第i个字符结尾的最长子串,f(i)=f(i-1)+1,如果第i个内容在之前没有出现过的话。如果出现过,记本次出现和上次出现的位置差为d,分为2种情况:
d<=f(i-1),也就是到上一个字符的最大子串长度比两个重复内容之间的长度要大,那么就要重新安排最大子串,比如qweraba,在计算最后一个a的时候,之前的最大长度已经是6了,而最后一个a与上一个a之间的距离是2,那么上一个a出现在f(i-1)的最长子串中,此时对应的最长无重复子串是’ba’,长度为2
d>f(i-1),也就是当前字符上次出现的位置在之前的最大子串之前,因此此时f(i)=f(i-1)+1,比如afabcacf,在分析最后一个元素f的时候,f(i-1)=2,上一步的最大无重复子串是ac,那么最终的最大无重复子串只需要加1,结果为3
具体代码如下:
1 | def getMaxStr(s): |
如果要返回这个最大子串,可以用一个list来存储当前的最大子串,最后返回
1 | def getMaxStr(s): |
面试题49:丑数
把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
思路:直观上,我们可以一个数一个数地判断,看看当前值是不是丑数。判断丑数的办法,因为丑数的因子只有2,3,5,那么他一直除以2,3,5最后一定为1,怎么判断有多少个2,多少个3,多少个5呢?方法是判断能被2整除的时候,就一直除以2;能被3整除的时候,就除以3;能被5整除的时候,就除以5。判断方法就是求余。
这种暴力方法虽然直观,但是时间复杂度太大了,无法通过系统测试。
还有一种方法就是以空间换时间,建立一个只存放丑数的数组ugly,既然我有第一个ugly的值,那么只要把这个值乘以2或3或5就可以得到下一个值,下一个值要保证最小,就是乘2,3,5之后最小的值。用3个index来表示乘以2,3,5的值的位置,要求乘以之后的新值一定要大于当前的最大值。
1 | # -*- coding:utf-8 -*- |
面试题50:第一个只出现一次的字符
在一个字符串(全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1(需要区分大小写).
用hash表的方法来实现。有了hash表,每次查询的时间复杂度为O(1),可以直接找到结果。因为char字符的大小是8位,一个char最多有256种可能,因此建立一个长度为256的数组,以char的ascii码为hash值,出现一个+1,再遍历一遍string,如果某一个char的出现次数为1,直接返回。
1 | class Solution: |
面试题51:数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。
直观思路是暴力法,时间复杂度为$\rm O(n^2)$
这道题的思路是归并排序,归并排序的时间复杂度为O(nlogn)
我们以数组{7, 5, 6, 4}为例来分析统计逆序对的过程。每次扫描到一个数字的时候,我们不能拿它和后面的每一个数字作比较,否则时间复杂度就是O(n^5),因此我们可以考虑先比较两个相邻的数字。
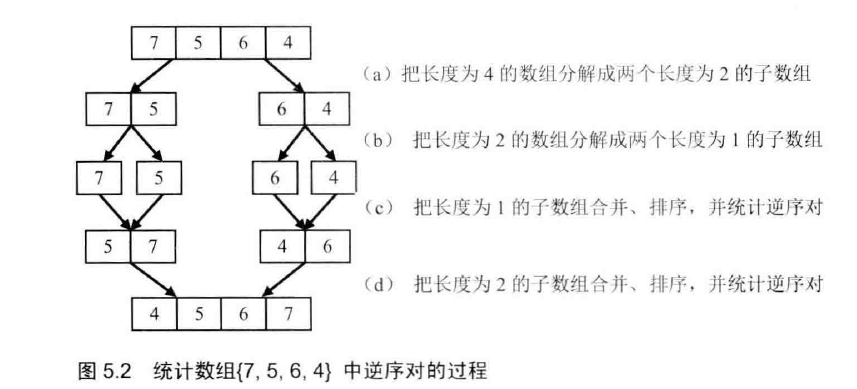
如图5 . 1 ( a )和图5.1 ( b)所示,我们先把数组分解成两个长度为2的子数组, 再把这两个子数组分别拆分成两个长度为1 的子数组。接下来一边合并相邻的子数组, 一边统计逆序对的数目。在第一对长度为1 的子数组{7}、{5}中7 大于5 , 因此(7, 5)组成一个逆序对。同样在第二对长度为1 的子数组{6}、{4}中也有逆序对(6, 4)。由于我们已经统计了这两对子数组内部的逆序对,因此需要把这两对子数组排序( 图5.1 ( c)所示),以免在以后的统计过程中再重复统计。
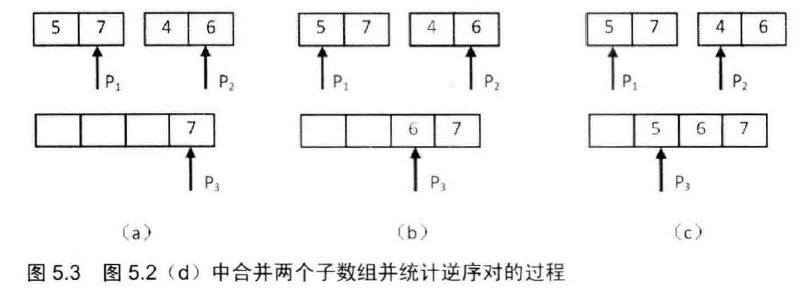
注 图中省略了最后一步, 即复制第二个子数组最后剩余的4 到辅助数组中.
(a) P1指向的数字大于P2指向的数字,表明数组中存在逆序对.P2 指向的数字是第二个子数组的第二个数字, 因此第二个子数组中有两个数字比7 小. 把逆序对数目加2,并把7 复制到辅助数组,向前移动P1和P3.
(b) P1指向的数字小子P2 指向的数字,没有逆序对.把P2 指向的数字复制到辅助数组,并向前移动P2 和P3 .
(c) P1指向的数字大于P2 指向的数字,因此存在逆序对. 由于P2 指向的数字是第二个子数组的第一个数字,子数组中只有一个数字比5 小. 把逆序对数目加1 ,并把5复制到辅助数组,向前移动P1和P3 .
接下来我们统计两个长度为2 的子数组之间的逆序对。我们在图5.2 中细分图5.1 ( d)的合并子数组及统计逆序对的过程。
我们先用两个指针分别指向两个子数组的末尾,并每次比较两个指针指向的数字。如果第一个子数组中的数字大于第二个子数组中的数字,则构成逆序对,并且逆序对的数目等于第二个子数组中剩余数字的个数(如图5.2 (a)和图5.2 (c)所示)。如果第一个数组中的数字小于或等于第二个数组中的数字,则不构成逆序对(如图5.2 (b)所示〉。每一次比较的时候,我们都把较大的数字从后往前复制到一个辅助数组中去,确保辅助数组中的数字是递增排序的。在把较大的数字复制到辅助数组之后,把对应的指针向前移动一位,接下来进行下一轮比较。
经过前面详细的诗论, 我们可以总结出统计逆序对的过程:先把数组分隔成子数组, 先统计出子数组内部的逆序对的数目,然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中,还需要对数组进行排序。如果对排序很熟悉,我们不难发现这个排序的过程实际上就是归并排序。
1 | # -*- coding:utf-8 -*- |
面试题52:两个链表的第一个公共节点
输入两个链表,找出它们的第一个公共结点。
直观思路依然是暴力法,但是暴力法通常不会是好办法。两个链表的长度分别为m和n,那么暴力法的时间复杂度为O(mn)
书中给出了两种思路:
方法1:利用2个辅助栈
如果两个链表有公共节点,那么最后一个节点是公共的(这道题的意思是只要两个链表有公共节点之后的所有节点都是相同的)。如果我们从后往前比较,那么一下就能找到结果。但是链表只能顺序访问,需要反向访问的时候,我们就借助栈来实现。
方法2:利用链表长度差
两个链表如果有公共节点,那么最后一个节点一定是一样的,那么我只要保证两个链表从同样的位置向后遍历即可找到公共节点。如下图,如果两个链表有公共节点,那么我们从2和4开始遍历,很容易找到6是公共节点并返回
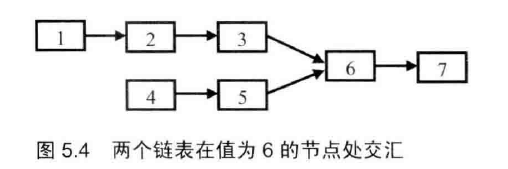
1 | # -*- coding:utf-8 -*- |
面试题53:在排序数组中查找数字
统计一个数字在排序数组中出现的次数。例如在排序数组[1,2,3,3,3,3,4,5]中查找3的出现次数,应该返回结果为4
因为是排序数组,自然想到二分查找。既然要找出现的次数,那么就要找到第一个出现的位置,和最后一个出现的位置。两者相减+1即得到出现的次数。
因此我们需要两个函数,getFirstK找到第一个出现的位置和getLastK找到最后一个出现的位置。
分别用二分查找进行实现这两个函数。
getFirstK的逻辑:
- 如果找到的中间值大于k,那么在左半部分查找
- 如果找到的中间值小于k,那么在右半部分查找
- 如果找到的中间值等于k:
- 如果当前值已经是第一个k出现的位置:也就是当前值的前一个值不为k或者此时的中间值已经是数组的第一个值,那么返回当前位置
- 其余情况在左半部分查找
getLastK的逻辑几乎相同。
1 | # -*- coding:utf-8 -*- |
题目2: 0~n-1中缺失的数字。
长度为n-1的递增排序数组中的所有数字都是唯一的,且每个数字都在0
n-1之内,在范围0n-1内的n个数字中有且仅有一个不在数组中,请找出该数字。
同样使用二分排序。
需要找的值一定是当前值不等于当前序号,但是上一个值等于上一个序号的情况。我们每次二分查找:
- 如果当前值等于当前序号,那么缺失值一定在右半部分;
- 如果当前值不等于当前序号:
- 如果上一个值等于上一个序号,返回当前值
- 如果上一个值不等于上一个序号,那么缺失值一定在左半部分
1 | def getMissingNum(data): |
题目3:数组中数值和下标相等的元素
假设一个单调递增的数组中所有元素唯一。请实现一个函数找出任意一个数值等于其下标的元素。如在[-3,-1,1,3,5]中,数字3与其下标相等。
同样,这道题还是使用二分查找。抓住数组是排序的这一特点,我们找到中间值:
- 如果中间值已经比序号小了,那么中间值左边的值肯定都比序号小,那就只用找中间值右边的值就行了
- 如果中间值比序号大,那么中间值右边的值一定都比序号大,那就只用找中间值左边的值就行了
1 | def getSameIndexNum(data): |
面试题54:二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中的第k小的结点。例如, (5,3,7,2,4,6,8) 中,按结点数值大小顺序第三小结点的值为4。
因为是二叉搜索树,因此中序遍历的结果就是从小到大排列的。只需要中序遍历直接拿结果就好了。
1 | # -*- coding:utf-8 -*- |
面试题55:二叉树的深度
给定一棵二叉树,写出求二叉树深度的函数。
二叉树深度只需要递归就可以求得。
1 | # -*- coding:utf-8 -*- |
题目2:平衡二叉树
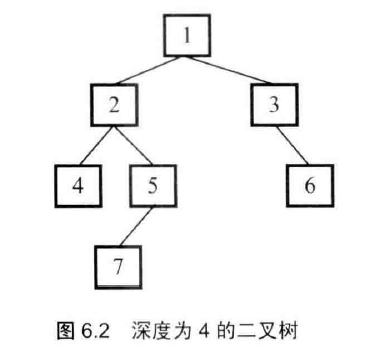
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果二叉树左右子树的深度相差不超过1,那么他就是平衡二叉树。
直观方法就是判断左右子树的深度,如果他们的深度差不超过1,那么继续判断他们子树是不是平衡二叉树,直到判断到最后一个节点。
这种方法存在大量的重复计算,如图,我们先判断以1为根节点的树是不是平衡的时候,我们要计算4,5,7这几个点,当判断以2为根节点的树是不是平衡的时候,我们依然要计算4,5,7这几个点,这就存在大量重复。
1 | # -*- coding:utf-8 -*- |
如果我们从下往上遍历,如果某个子树是平衡二叉树,就返回其深度,否则停止遍历,这样就减少了不必要的开销。
1 | class Solution: |
面试题56:数组中数字出现的次数
题目一:数组中只出现一次的两个数字
一个数组里除了两个数字以外,其余数字都出现了2次。请找出这两个只出现了一次的数字,要求时间复杂度为O(n),空间复杂度为O(1)
这道题的难点在于限制了时间和空间复杂度。我们不妨先考虑他的简单版本,如果一个数组中有一个数只出现了1次,而其余数出现了2次,找到这一个数字可以用什么方法呢?
找寻的技巧就是异或,如果所有元素异或起来,出现两次的元素一定被消除了,最后就剩下一个只出现了一次的元素。
那么两个元素的时候怎么办呢?就要把这个数组分为两部分:每一部分只包含一个出现了1次的元素,且出现两次的元素一定在同一个子数组中。那么怎么划分呢?
我们把所有元素异或起来,因为另外两个元素不相同,那么以后之后的结果至少有一位不为0,我们找到这个不为0的位。再遍历原数组,按照这一位为0和不为0分成两个数组,由于出现两次的元素某一位肯定是要么同时为0,要么同时为1,也就是划分到同一个子数组中了,就符合要求了。
1 | def findOneIndex(resultXOR): |
题目2:数组中唯一出现的数字
一个数组中,除一个数字只出现一次之外,其余数字都出现了3次,找出这个只出现了一次的数字。
虽然这道题不能用异或运算(因为抑或运算3个相同的值得到的肯定是本身),但是可以参考上面的思路。
我们按位求和,出现三次数字的那一位一定是3的倍数,那么让每一位对3求余,余数一定是多出来那个数所带来的。
1 | def findNumAppearOnce(data): |
面试题57:和为s的数字
题目1,:和为s的两个数字
输入一个递增排序的数组和一个数字s,在数组中查找这两个数,使得他们的和刚好是s,如果有多对数字的和为s,输出其中一对即可。
如果使用暴力法,时间复杂度为$O(n^2)$
正确的方法是使用两个指针,一个指向数组最前面,一个指向最后面,因为数组是排好序的
- 如果a+b<target,那么表示a太小了,a指针向后移动
- 如果a+b>target,证明值太大了,b指针向前移动
1 | # -*- coding:utf-8 -*- |
题目2:和为s的连续正数序列
输入一个正数s,打印出所有和为s的连续正数序列(至少包含两个数),例如输入15,由于15=1+2+3+4+5=4+5+6=7+8,所以打印出三个序列[1-5,4-6,7-8]
两个指针,一个指向1,一个指向2
- 如果和小于目标,右侧指针+1
- 如果和大于目标,左侧指针+1
终止条件是左侧指针>(1+target)/2,因为当左侧指针等于(target-1)/2的时候,题目至少包含两个数的要求,下一个数是(target+1)/2,两者之和是target。
求和有个小技巧,就是利用一个curSum变量来存储和,如果大了就减掉左边的值,如果小了,就加上右边的值。
1 | # -*- coding:utf-8 -*- |
面试题58:旋转字符串
题目1:翻转单词顺序
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。比如输入“I am a student.”,翻转之后得到”student. a am I”
这道题利用python的spilit方法很容易做出来" ".join(s.split(" ")[::-1]),但是这样并不是这道题考察的核心,要通过这道题的考察,我们需要看看剑指offer上面的方法。
书中给出的方法是翻转2次,第一次翻转所有内容,第二次只单独翻转单词。
1 | # -*- coding:utf-8 -*- |
题目2:左旋转字符串
左旋转操作就是把字符串前面的若干个自负转移到字符串尾部。请定义一个函数实现字符串的左旋转操作。比如,输入字符串”abcdefg”和数字2,输出”cdefgab”
和上面问题的解法类似,将字符串分为两个部分,前n个和后面部分,先翻转前n个,再反转后面部分,再整体翻转,就得到了想要的结果。
1 | def reverseAll(s): |
面试题59:队列的最大值
题目1:滑动窗口的最大值
给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。例如,输入数组[2,3,4,2,6,2,5,1],滑动窗口大小为3,那么一共存在6个滑动窗口,他们的最大值分别为[4,4,6,6,6,5]
思路:这道题的思路主要是用一个队列暂存可能是最大值的元素的index,根据当前遍历的值与已暂存的值的关系,决定已暂存值删除头部或尾部,并将当前最大值存入另一个专门用于存放最大值的队列中。
这样说可能有些抽象,我们用上面这个例子来说明。
定义两个队列,一个是result,存放返回的最大值,一个是temp,暂存最大值。
temp首先存入2,然后存入3,由于3比2大,窗口中的最大值不可能为2,所以在temp中删除2,压入3。
然后存入4,由于4比3大,同理删除3,压入4.
继续,存入2,由于4比2大,在4出栈后,2可能成为最大值,因此不删除元素,直接压入2,此时temp里面的内容为4,2
下一步存入6,由于6比4和2都大,因此把4,2都删了,压入6。
接下来压入2,压入5,删除2。再压入1,此时因为6的index与1的index差已经大于等于3了,要删除掉6,此时temp的结果为5,1
每次遍历一个元素的时候,我们都要将temp[0]压入result中,最终返回result即可。
1 | class Solution: |
题目二:队列的最大值
定义一个队列并实现函数max得到队列的最大值,要求函数max,push_back和pop_front的时间复杂度都是O(1)
思路与前面问题一的思路相同,用一个maxnum队列来存储最大值。
抽象建模能力
面试题60:n个骰子的点数
题目:把n个骰子扔在地上,所有骰子朝上的点数之和为s,输入为n,打印出s所有有可能的值出现的概率
这道题很容易想到的方法是递归,但是递归的时间效率比较低,所以更好的方法是循环。递归的代码如下。
getTouziCore(origin, now, sumv, result)这个函数的功能是一共有origin枚骰子,现在还剩下now枚,总值是sumv,所有结果放在result里面。result数组的长度为6*n+1(最后一个值为6n),最终需要的部分是[n:]这部分。
1 | def getTouziCore(origin, now, sumv, result): |
基于循环方法的思路是这样的:假设我们现在有一个骰子,那么可能出现的点数是1-6,每个出现的次数都是一次,记作f(i)=1,i=1-6再来一个骰子。每种点数出现的次数是f(n-1)+f(n-2)+f(n-3)+f(n-4)+f(n-5)+f(n-6),因此用两个list来存放值,,last存放上一次的可能出现值的结果,this存放本次的结果。代码如下:
1 | def getTouziSum(n): |
java版本:
1 | public static int[] touzi(int n) { |
面试题61:扑克牌中的顺子
题目:从扑克牌中随机抽5张牌,并判断是不是一个顺子。
先排序,统计其中0的个数,从最后一个0的下下个元素开始遍历,如果当前元素与上一个元素的差值不是1,那么就用0来填充,只要最后0的数量大于等于0,那就是刚好填充完或者0还可以放在最前面或者最后面,此时返回true,其余情况返回false
1 | # -*- coding:utf-8 -*- |
java版本
1 | //1. 除0以外没有重复数字 |
面试题62:圆圈中最后剩下的数字
题目:0,1,…,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈中删除第m个数字,求出圆圈中最后剩下的一个数字。
思路:有两种思路,一种是用循环链表模拟这个圆圈,这种思路要用c++实现,因为python没有指针,实现起来不方便。
还有一种思路是通过找数学规律来的,这个问题是著名的约瑟夫问题,其推导公式是f(n,m)=[f(n-1,m)+m]%n,f(n,m)表示的是从n个数中删除m个最后剩下的值。最后的实现代码如下。
1 | # -*- coding:utf-8 -*- |
java版本:
1 | public static int restNum(int n, int m){ |
面试题63:股票的最大收益
题目:假设把某只股票的价格按时间顺序存储在数组中,请问买卖这只股票一次获得的最大收益是多少?例如某只股票的价格是[9,11,8,5,7,12,16,14],如果在价格5的时候买入,并在价格为16的时候卖出,则获得最大收益11.
用暴力法很简单,直接遍历到每个元素的时候,都与前面的元素相减即可,这样做的时间复杂度为$O(n^2)$。
改进的方法是抓住题目要求,要求是获得最大收益,那么我们只要用当前值,减去前面所有元素中的最小值就可以得到当前的最大收益。我们只需要用一个变量来存储之前的最小元素,一个变量存储最大收益,最终返回最大收益即可。
1 | def getMaxIncome(nums): |
发散思维能力
面试题64:求1+2+…+n
求1+2+…+n,要求不能使用乘除法,for,while,if,else,switch,case等关键字及条件判断语句(a?b:c)
c++可以用构造函数等方法来求解,python可以用and运算的短路机制来实现。
1 | # -*- coding:utf-8 -*- |
面试题65:不用加减乘除做加法
题目:写一个函数,求两个整数之和,要求函数体内不得使用+,-,*,/等符号
既然不能用四则运算,那么就只能考虑位运算,我们先来看看一个加减乘除是怎么做的。例如,计算5+17,先计算各位之和,5+7=12,不考虑进位的情况,个位为2,十位还是为1,接下来再考虑进位,1+1=2,结果是22.
我们换成二进制来看看,5的二进制是101,17的二进制是10001,依然是三步:第一步相加不计进位,第二步记录仅为,第三步把前两部的结果相加。
由于python当中左移运算可能溢出,所以返回的时候要判断是否为负数,如果为负数就返回按位取反的结果。
1 | # -*- coding:utf-8 -*- |
面试题66:构建乘积数组
题目:给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中b的元素B[i]=A[0]*A[1]*…*A[i-1]*A[i+1]*…*A[n-1],要求不能使用除法
如果能使用除法,那么这道题变成先计算A[0]~A[n]的累积,然后每次除以A[i]即可找到B[i],如果不能使用除法,直接暴力乘积的话,时间复杂度O(N^2)
要找到简便方法,那就是用两个数组C和D来存储左半部分的乘积结果和右半部分的乘积结果。C[i]=A[0]*A[1]*…*A[i-1],D[i]=A[i+1]*…*A[n-1]
这两个数组又分别可以通过循环迭代出来,C[i] = C[i-1]*A[i-1],D[i]=D[i+1]*A[i+1],C数组可以从小到大求得,D数组可以从大到小求得。然后分别相乘得到结果。这样省去了中间每一步计算累积的时候的重复计算。
1 | # -*- coding:utf-8 -*- |
补充知识
B+树和B树的区别
要理解b树,首先要理解平衡二叉树
平衡二叉树特点:(总的来说就是左右子树深度不超过1的二叉排序树)
(1)非叶子节点最多拥有两个子节点;
(2)非叶子节值大于左边子节点、小于右边子节点;
(3)树的左右两边的层级数相差不会大于1;
(4)没有值相等重复的节点;
2、B树(B-tree)
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),数据库索引技术里大量使用者B树和B+树的数据结构。

3、B+树
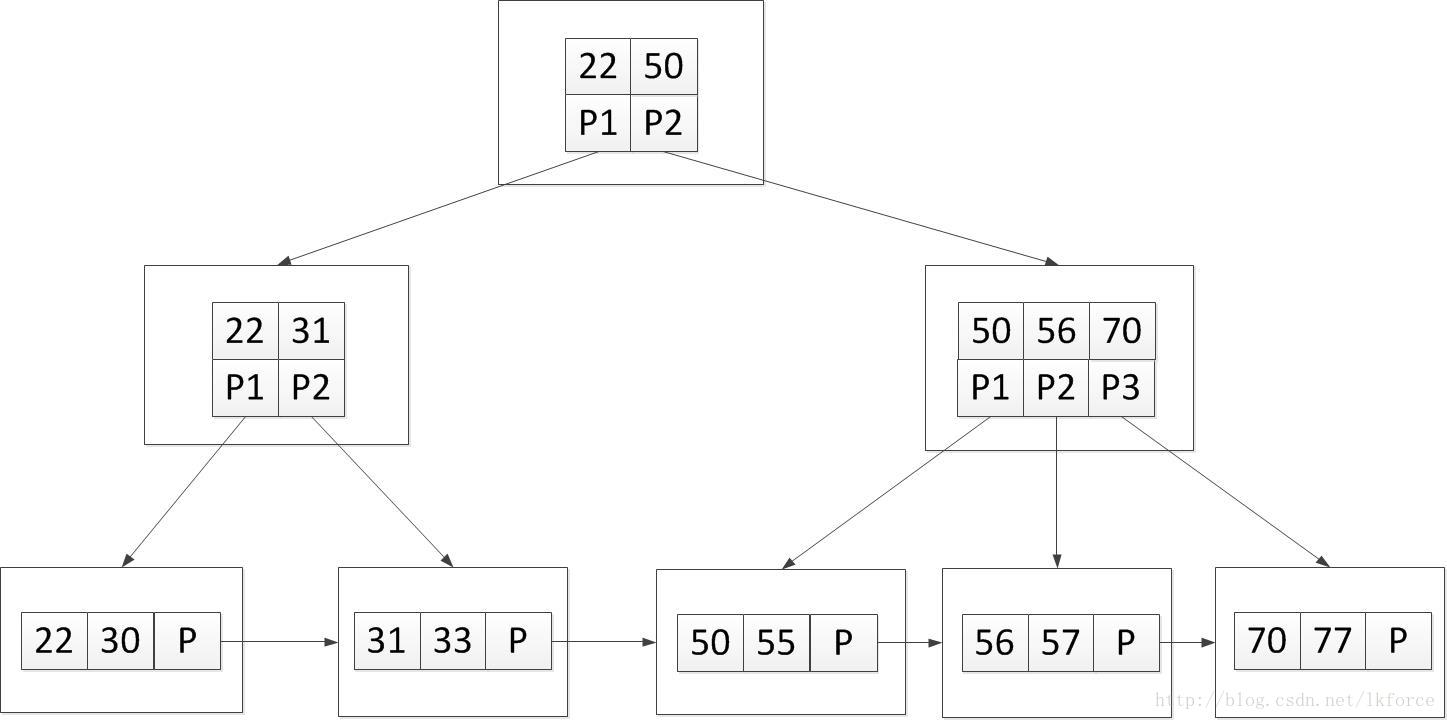
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别
两者的区别:
- B树的每个结点都存储了key和data,而B+树的data存储在叶子节点上,节点不存储data,这样一个节点就可以存储更多的key。可以使得树更矮,所以IO操作次数更少。
- B+树的所有叶结点构成一个有序链表,可以按照关键字排序的次序遍历全部记录。由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。相邻的元素可能在内存中不相邻,所以缓存命中性没有B+树好。
输入网址到页面出现的过程
- DNS解析
- TCP连接
- 发送HTTP请求
- 服务器处理请求并返回HTTP报文
- 浏览器解析渲染页面
- 连接结束
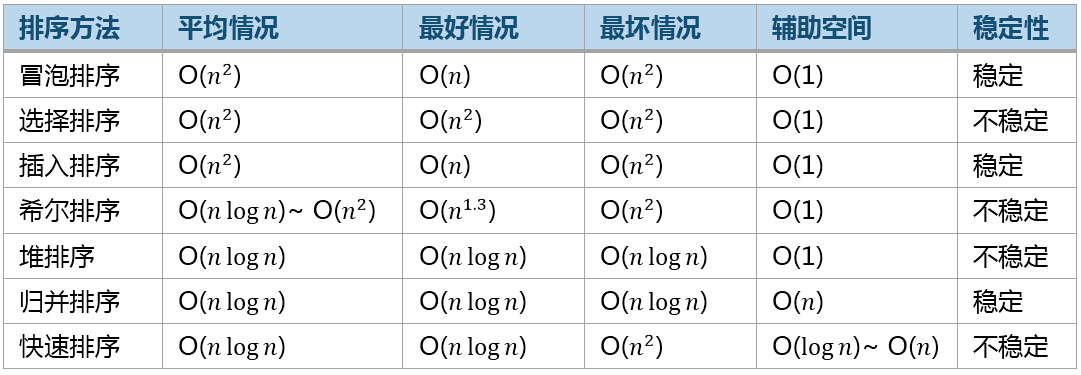
常见排序算法复杂度
子矩阵最大和
给定一个矩阵,求子矩阵的最大和
这道题其实是数组最大和的扩展版本,具体实现方式是一个i循环,一个j循环,表示的是从第i行到第j行的子矩阵,每过一行,把上一行的每一列的值加到下一行,再用一维数组求最大和的方式就可以得到结果。
1 | public class MaxSubMatrix { |
也可以直接每次把中间值记录下来:
1 | public static int maxSubMatrix(int[][] matrix) { |
背包问题
两种背包问题做法类似,都是先枚举物品,再枚举容量,不同点在于完全背包问题要从小到大枚举容
量,0/1 背包问题要从大到小枚举容量。
直方图最大矩形面积
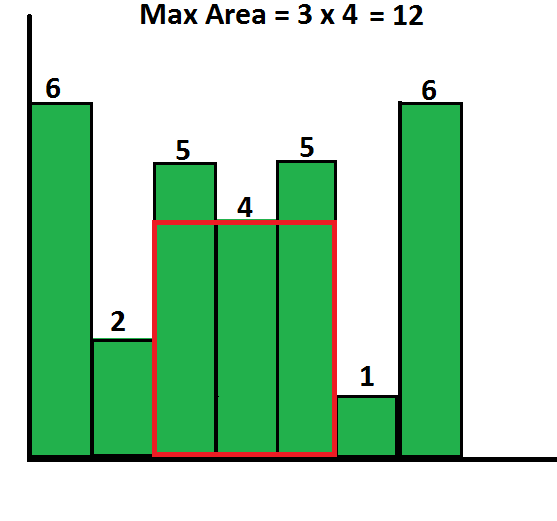
两种方法
单调栈:维护一个单调递增的栈,如果发现一个比栈顶元素小的值,栈顶元素出栈,计算栈顶元素对应的矩形面积。遍历完整个直方图数组,如果栈里还有元素,依次出栈计算面积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public static int maxRect(int[] hists) {
if (hists == null || hists.length == 0) {
return 0;
}
int max = 0;
Stack<Integer> stack = new Stack<>();
int i = 0;
while (i < hists.length) {
if (stack.isEmpty() || hists[stack.peek()] <= hists[i]) {
stack.push(i++);
} else {
int top = stack.pop();
int area = hists[top] * (stack.isEmpty() ? i : i - stack.peek() - 1);
max = Math.max(max, area);
}
}
while (!stack.isEmpty()) {
int top = stack.pop();
int area = hists[top] * (stack.isEmpty() ? i : i - stack.peek() - 1);
max = Math.max(max, area);
}
return max;
}
提前计算左右边界:
对于i,left[i]表示左边第一个比i小的元素的位置,right[i]表示右边第一个比i小的元素的位置
1 | public static int largestRectangleArea1(int[] heights) { |
有一个trick在这里,每次j—或者j++这样的效率很低,复杂度是O(n^2),如果利用已经算好的结果就会快很多,j--改成j=left[j],j++改成j=right[j],解释一下这两个公式的含义,比如{1,10,11,9,3}这个数组,在计算3的left的时候,发现9比3大,left[9]其实已经算出来是1了,所以直接跳到1,这是因为9都比3大了,那么比9大的10和11肯定也比3大,同理right数组也是一个道理。
最大子矩阵
如下图:给定一个由1,0组成的矩阵,求其中最大的全为1的子矩阵
1 | Input: |
思路:其实这道题的思路和求直方图最大面积很像,把每一行看做一个直方图,找到当前行所有列的高度,然后求最大面积即可。height数组表示直方图的高度,left表示左边第一个比i小的位置,right数组表示右边第一个比i小的位置。面积就等于(height[i]*(right[i]-left[i]-1)),为什么这个长度是right[i]-left[i]-1呢,是因为本来满足条件的个数是right[i]-1-(left[i]+1)+1,刚好就是前面的结果。
1 | public static int maximalRectangle(char[][] matrix) { |
水塘抽样
一个流式数据集,不知道最终会有多少个数据,要求从这些数据中抽出k个,并且每个元素被抽到的概率相同。
这个问题被归纳为水塘抽样问题,用一个大小为k的池子,先一个一个放进去,放满之后,下一个元素放进去的概率是
k/(k+i),那么对于之前就在水池里面的元素X,他仍然被保留在水池中的概率是
p(X之前就在水池中)*p(X在k+i这个数据到来的时候没有被替换掉)=p(X之前就在水池中)*(1-p(X在k+i这个数据到来的时候被替换掉))
=p(X之前就在水池中)*(1-p(k+i被留下来,并且替换掉了X))
=k/(k+i-1) * (1-k/(k+i)*1/k)=k/(k+i)
因此此时所有元素被选中的概率都是k/(k+i),当k+i=n的时候,所有元素被选中的概率都是k/n。